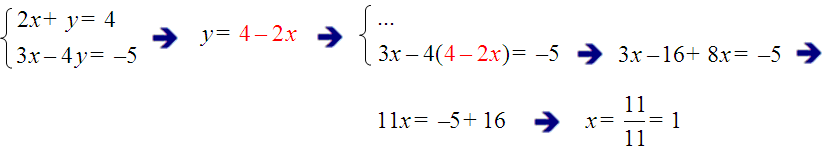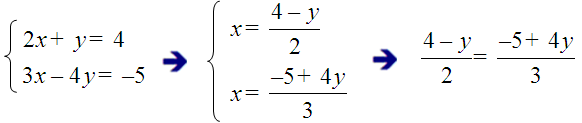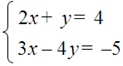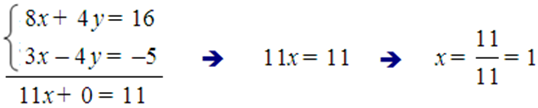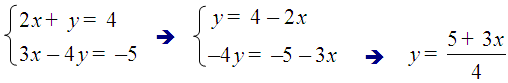2.3.1 Métodos de resolución de sistemas de ecuacións lineais

Hai catro métodos (ou técnicas) de resolución dun sistema: substitución, igualación, redución e representación gráfica

Método de substitución

Despexamos unha incógnita nunha ecuación e substituímos o seu valor na outra ecuación.

• Exemplo.

A incógnita máis doada de despexar é a y da primeira ecuación:

E agora substituímos este valor de x en calquera das ecuacións para despexar a outra incógnita; o máis fácil é facelo na ecuación y = 4 - 2x:

A solución do sistema é x = 1, y = 2.

 

Método de igualación

Despexamos a mesma incógnita nas dúas ecuacións e logo igualamos os resultados.

• Exemplo:

Multiplicamos en cruz:

E o valor de y = 2 obtido substituímolo en calquera das ecuacións do principio; neste caso o máis doado é facelo nesta ecuación:

Obtemos a mesma solución que co método da pregunta anterior, como é lóxico.

Método de redución

Neste método multiplicamos as dúas ecuacións por números adecuados de xeito que os coeficientes dunha das incógnitas teñan valores opostos nas dúas ecuacións.

• Vexamos como se fai co mesmo sistema anterior:

E agora sumamos as dúas ecuacións membro a membro:

E o derradeiro paso é substituír este valor de x = 1 en calquera das ecuacións anteriores para calcular o valor de y; por exemplo, en 2x + y = 4:

O sistema está resolto.

Interpretación gráfica da solución dun sistema de ecuacións

Os métodos de substitución, igualación e redución son métodos alxébricos, e son os que usamos habitualmente. Pero hai un cuarto xeito de achar a solución (ás veces menos preciso), o método gráfico.

Se en cada ecuación do sistema despexamos a y obteremos dúas funcións lineais. A representación gráfica desas funcións son dúas liñas rectas, que se cortarán nun punto: as coordenadas deste punto son os valores de x e y da solución do sistema, xa que nese punto os valores de x e y satisfacen simultaneamente as dúas ecuacións.

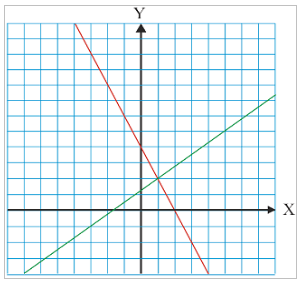
• Exemplo. Sexa o sistema:

Facemos as táboas de valores x,y para as dúas funcións lineais obtidas e representamos:

y = 4 - 2x
x	y	x	y
-3	10	-3	-1
4	4	1	2

 

O punto de corte das rectas é o (1,2), así que a solución do sistema é x = 1, y = 2

Que ocorrería se as dúas rectas resultasen ser paralelas? Non habería punto de corte e o sistema de ecuacións non tería ningunha solución: sería un sistema incompatible.