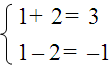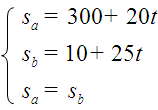2.3 Sistemas de ecuacións lineais

Que son os sistemas de ecuacións lineais?

Unha ecuación é lineal cando é de grao 1 respecto de todas as incógnitas, e non hai produtos nin divisións entre elas; así,

3x + 2y - 8 = 0 é unha ecuación lineal.

3x² - 2y - 5 = 0 non é unha ecuación lineal.

3xy + 8y = 8 tampouco é unha ecuación lineal.

Un sistema de dúas ecuacións lineais con dúas incógnitas ten a forma xeral:

Onde x e y son as incógnitas, e a, b, c, a', b', c' son os coeficientes e termos independentes (números normalmente).

Resolver o sistema de ecuacións lineais consiste en atopar os valores das incógnitas que fan certas as dúas ecuacións simultaneamente. Por exemplo:

Neste sistema a solución é x = 1 e y = 2, xa que fan verdadeiras as dúas igualdades:

A maioría das veces os sistemas de ecuacións teñen unha única solución (un valor para cada incógnita), pero pode ocorrer tamén que o sistema non teña ningunha solución e mesmo que teña infinitas. Para resolver algúns problemas de móbiles precisamos os sistemas de ecuacións lineais. Vexamos un exemplo:

• Un coche está na posición inicial s_o = 300 m e móvese a 20 m/s. Un motorista está inicialmente na posición 10 m e persegue o coche cunha velocidade de 25 m/s. Onde e cando o alcanza?

• Solución.

Datos do coche (A): s_o = 300, v_a = 20

Datos da moto (B): s_o = 10, v_b = 25

Aplicamos a ecuación da posición do movemento uniforme (s = s_o + v.t) aos dous móbiles: s_a = 300 + 20.t; s_b = 10 + 25.t

No momento do alcance, os dous móbiles están na mesma posición, polo tanto a condición será s_a = s_b. Reunindo todas as ecuacións, temos tres incógnitas (s_a, s_b, t) e tres ecuacións: isto é un sistema de ecuacións lineais.

No que segue aprenderemos como resolvelos.