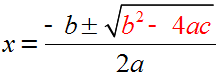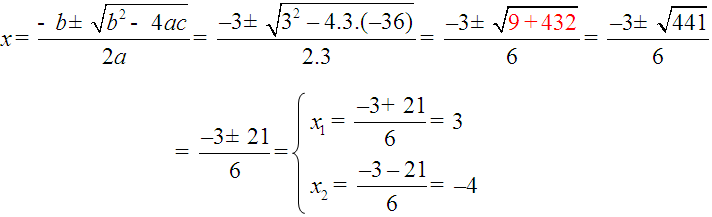2.2.2 Número de solucións dunha ecuación de segundo grao
Unha ecuación de segundo grao pode ter dúas solucións, unha ou ningunha, e iso depende do valor do discriminante, a expresión b2 - 4ac, que é a parte vermella que está dentro da raíz cadrada na ecuación:
Se o discriminante é positivo, b2 - 4ac > 0, a ecuación ten dúas solucións distintas; se o discriminante vale cero a ecuación ten unha solución (ou dúas de igual valor, que vén sendo o mesmo); e se o discriminante é negativo, b2 - 4ac < 0, a raíz cadrada non se pode calcular (con números reais) e a ecuación non ten ningunha solución.
-
Exemplos.
-
A ecuación x2 + 3x + 10 = 0 non ten ningunha solución, porque:
-
A ecuación 2x2 + 12x + 18 = 0 ten unha soa solución, porque:
A solución única x = - 3 tamén se chama solución dobre.
-
A ecuación 3x2 + 3x - 36 = 0 ten dúas solucións distintas:
S8. Determine, coa axuda do discriminante, cantas solucións ten cada ecuación:
|
3x2 - 6x + 3 = 0 |
x2 + x - 3 = 0 |
x2 + x + 3 = 0 |
-x2 - 2x - 3 = 0 |
2x2 + 5x + 1 = 0 |
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0