6.2. Solucións actividades complementarias
S16.
Non oiremos nin un son nin outro, xa que o son no se pode propagar no baleiro.
S17.
Sabemos que v = e/t e que t = e/v. Para percibir o eco, o son ten que facer un percorrido de 17 m de ida e outros 17 m de volta ata o emisor, polo que o espazo total será de 34 m, e así temos: t = 34 / 340 = 0,1 s.
S18.
Non poderiamos escoitar as badaladas a distancia ningunha, xa que o son non se transmite no baleiro.
S19.
O son viaxa polo aire a 340 m/s. En medios materiais máis densos que o aire alcanza velocidades superiores. Nos medios sólidos é onde o son alcanza maior velocidade, xa que as súas partículas están máis próximas que nos líquidos e nos gases, esta proximidade das partículas facilita a transmisión de unhas a outras.
Nos materiais elásticos os átomos están relativamente xuntos e responden con prontitude aos movementos dos demais, polo que transmiten enerxía con poucas perdas. Este é o caso da plastilina.
S20.
Porque emiten ultrasóns que se reflicten na presa e volven a ser captadas polo morcego, que así calcula a distancia á que está a presa.
S21.
|
A |
|
|
G |
|
|
B |
|
D |
|
|
|
C |
|
A |
|
|
|
D |
|
F |
|
|
|
E |
|
C |
|
|
|
F |
|
B |
|
|
|
G |
|
E |
|
S22.
O limiar da dor corresponde a unha intensidade de 120 dB.
S23.
Sabemos que e = v.t; daquela e = 340 m/s. 7 s = 2.380 m.
S24.
Negra.
S25.
É certo, xa que as vibracións sonoras do piano pasan ás partículas do bastón e delas ás partículas óseas da persoa. As vibracións producidas pola fonte sonora (neste caso o piano) transmítense ata chegar á persoa.
S26.
-
Unha cámara anecoica ou anecoide é unha sala especialmente deseñada para absorber o son que incide sobre as paredes, o chan e o teito da cámara, anulando os efectos do eco e a reverberación do son.
-
A cámara anecoide íllase do exterior cunhas paredes recubertas con cuñas en forma de pirámide coa base apoiada na parede, construídas con materiais que absorben o son. Entre estes materiais están a fibra de vidro e a espuma.
S27.
Sabemos que n = c/v; daquela n = 300.000/220.558 = 1,36
S28.
Sabemos que e = v.t; Daquela e = 340.0,8 = 272 m. 272m é a distancia de ida e volta que percorre o son; por tanto, a distancia ao fondo do val é 272/2 = 186m.
S29.
Sabemos que e = v.t; daquela e = 1500.0,3 = 450 m é a distancia de ida e volta que percorre o son; por tanto a distancia ao fondo do mar é 450/2 = 225 m.
S30.
Debido á enerxía que transportan as ondas do son, enerxía cinética, que é a asociada ao movemento.
S31.
a) 3x = 36
b) ![]()
c) 2x + 20 =16
d) ![]()
e) 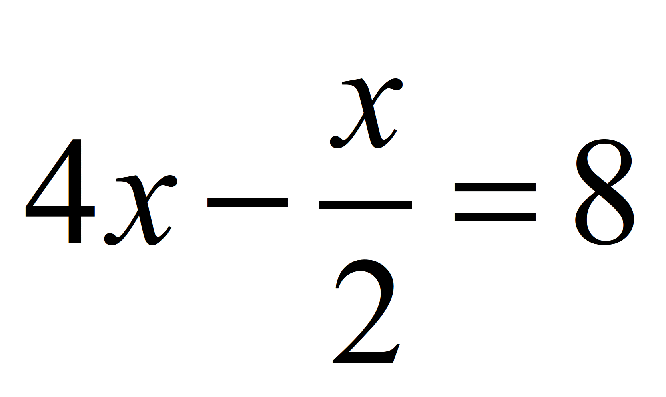
S32.

S33.

S34.
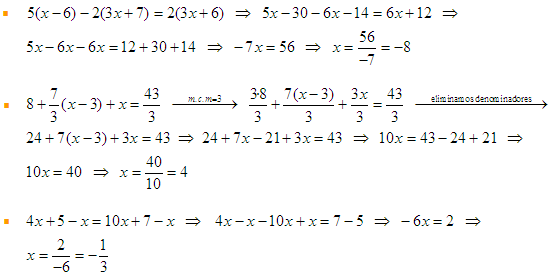
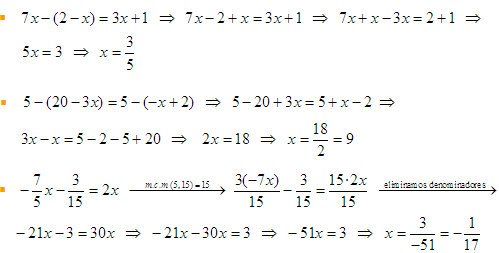
S35.
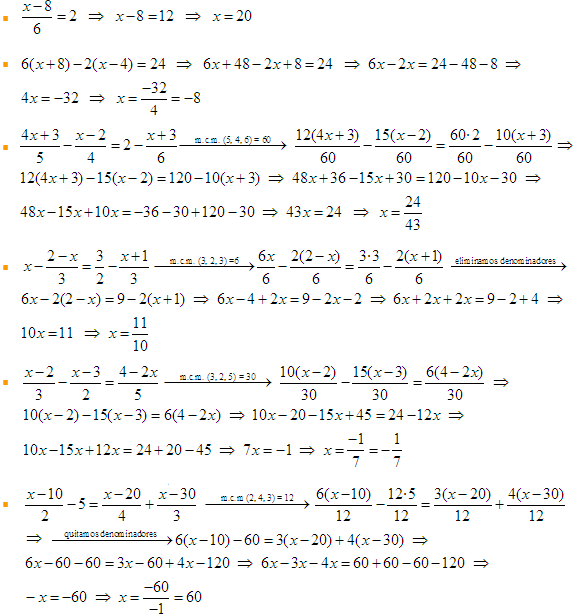
S36.
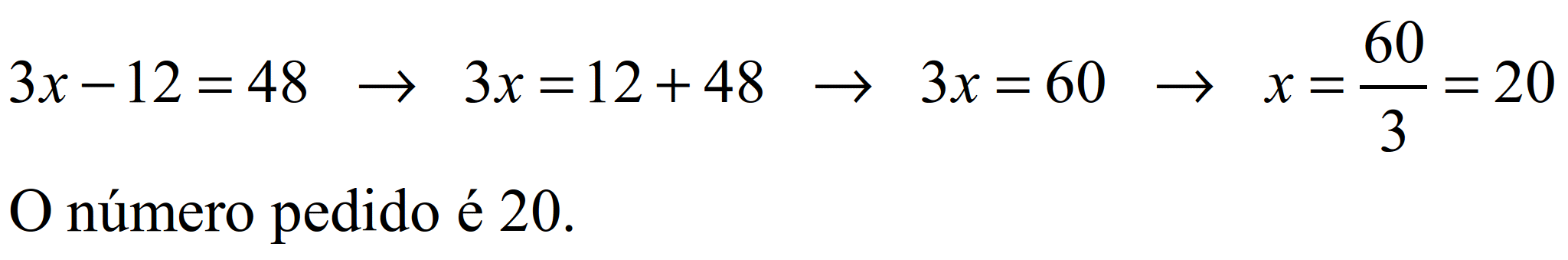
S37.
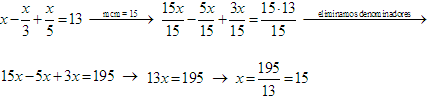
S38.
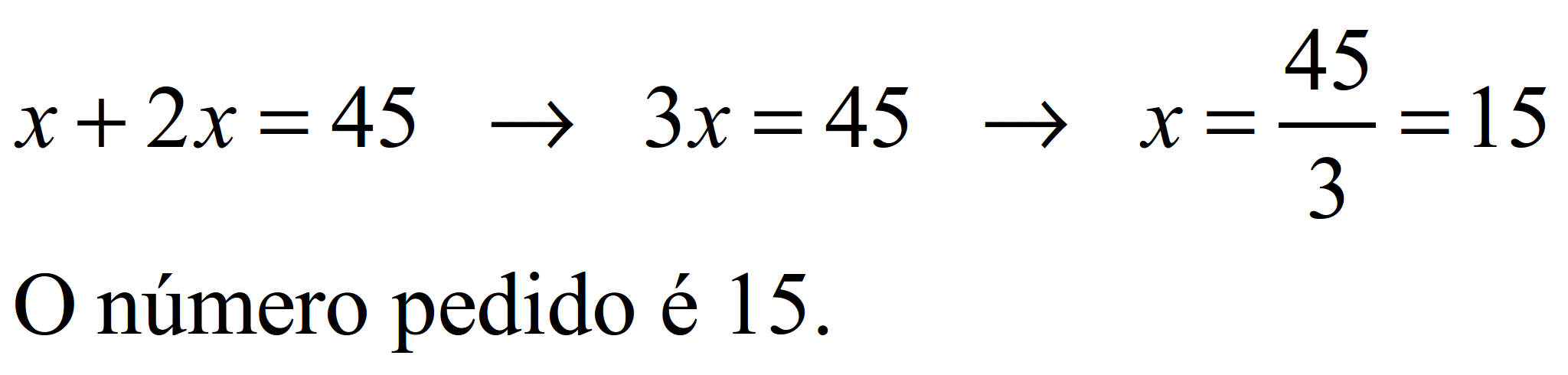
S39.
Sexa x a altura do rectángulo. A base mide entón x + 2. Daquela o perímetro mide x + x + (x+2) + (x+2) = 4x + 4, e isto ten que dar 400; daquela:
![]()
Os lados miden 99 m e 101 m respectivamente.
S40.
Consecutivos significa “seguidos”, como 13 e 14, por exemplo. Se un dos número é x, o seguinte é x + 1; por tanto:
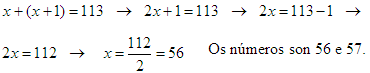
S41.
Un quilogramo de mazás custa 0.50 euros máis que un de laranxas. Edelmira mercou tres quilogramos de laranxas e un de mazás por 5.30 euros. A como están as laranxas? E as mazás?
Sexa x o prezo dun quilogramo de laranxas; un quilogramos de mazás custa entón x + 0,50. O importe da compra é:
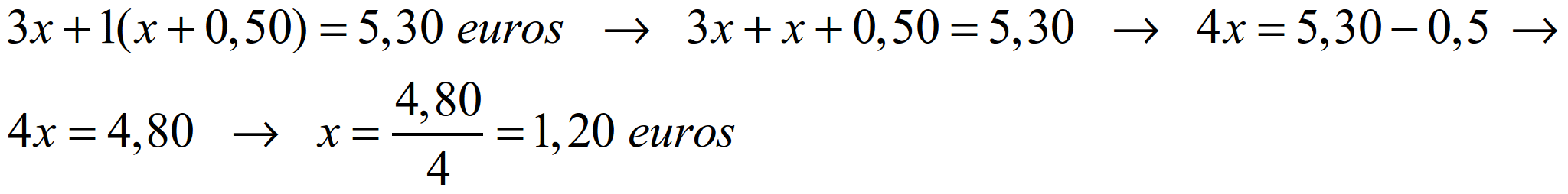
As laranxas custan 1,20 euros cada quilogramo, e as mazás custan 1,70 euros cada quilogramo. Comprobación:
3 kg de laranxas custan: 3·1,20 = 3,60 EUR1 kg de mazás custa: 1·1,70 = 1,70 EUR.
Total compra = 5,30 EUR
S42.
Cada semana aforra 50 euros. Sexa x o número de semanas que ten que aforrar; xa que logo:
![]()
S43.
A multa son 105 euros. Sexa x o número de días de atraso en pagar a multa; o recargo é 3·x, logo o importe total da multa será 105+3x:
![]()
S44.
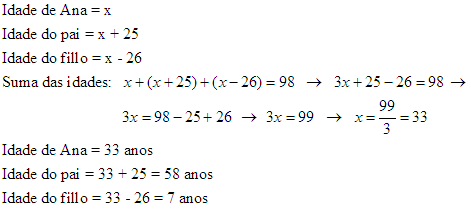
S45.
O perímetro da leira é a suma dos seus catro lados: x +2x +x +2x = 6x, e isto ten que ser 210 metros de arame; por tanto:
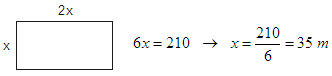
Os lados miden 35 m e 70 m respectivamente.
S46.
Número buscado: x. Daquela:
![]()
S47.
Se un número é x, o outro ten que ser 100–x, xa que entre os dous suman 100; agora escribimos en linguaxe alxébrica que a súa diferenza é 44:
![]()
Un número é 72 e o outro é 28
S48.
Número de leóns: x; número de tigres: 2x (hai o dobre). Escribimos a ecuación:
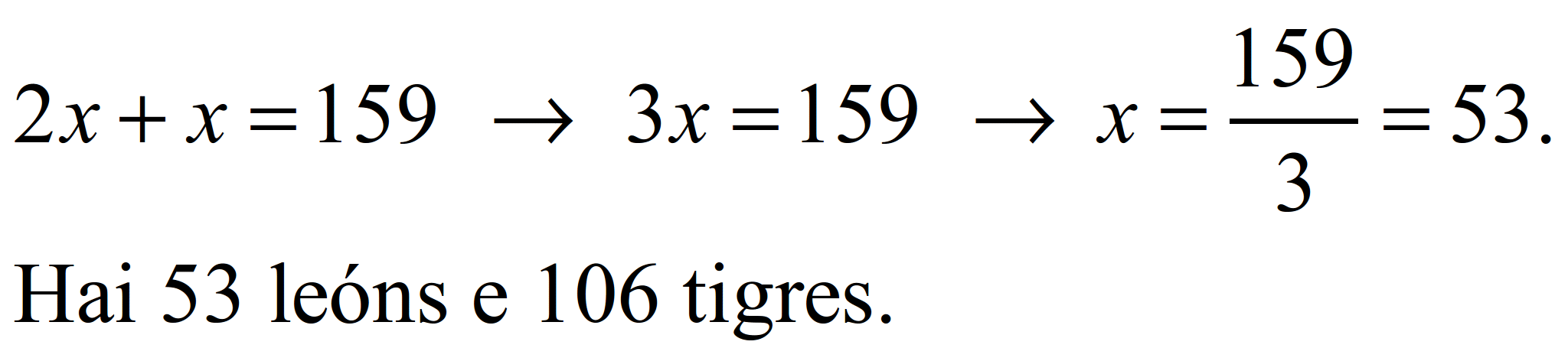
S49.
Os tres números consecutivos (seguidos) son x, x+1 e x+2. A suma dos tres números vale 141, daquela:
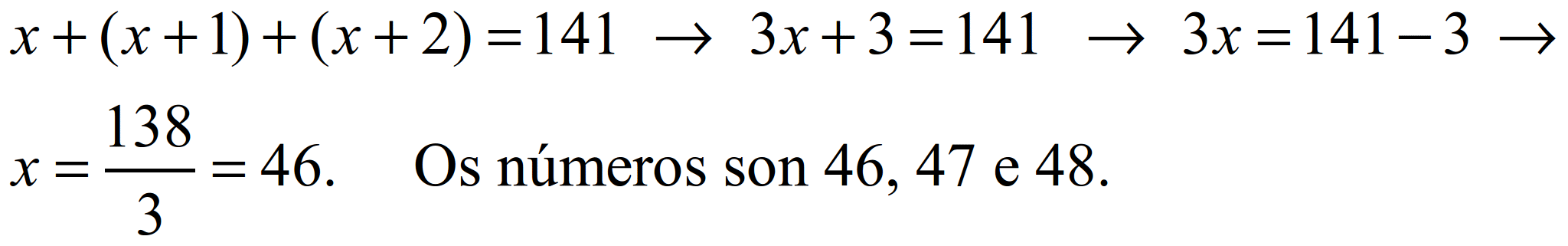
S50.
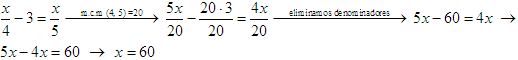
S51.
Prezo dunha leituga: x; prezo dun repolo: x+0,10 (lembre que 10 céntimos de euro son 0,10 euros). Tres leitugas mais catro repolos son seis euros; escribimos isto na linguaxe alxébrica e resolvemos a ecuación:
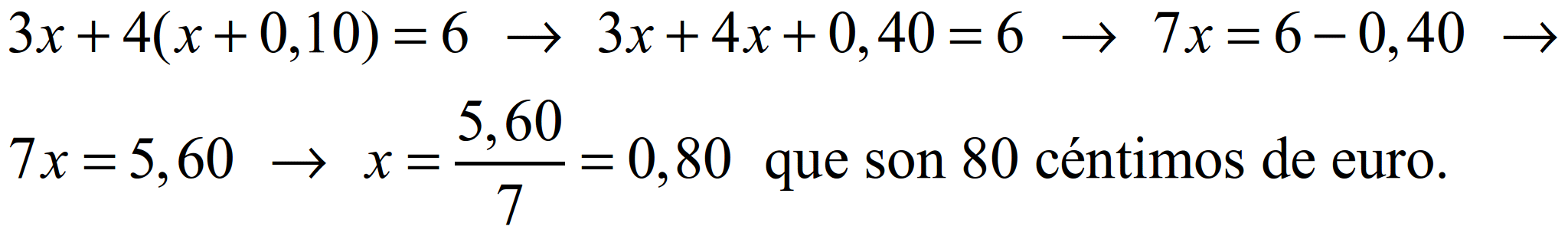
A leituga custa 80 céntimos e o repolo 90 céntimos.
S52.
Un número é x; o outro é x/4. A suma dos dous números é 50; entón:
![]()
![]()
Un número é 40; o outro é 10 (40:10)
S53.
Cartos que leva C: x
Cartos que leva B = x+200
Cartos que leva A = 200 + (x+200)
A suma dos cartos é 3.201 euros, con isto escribimos unha ecuación:
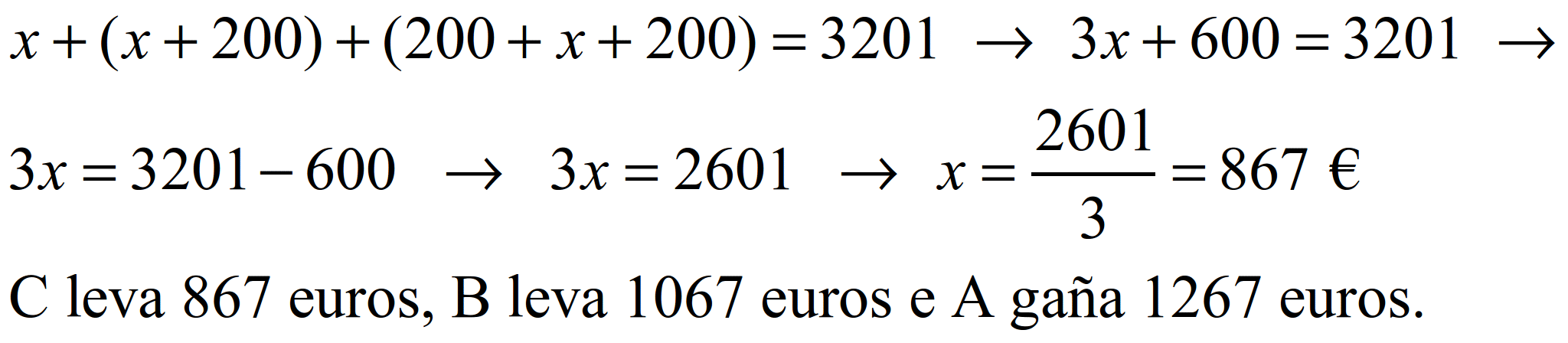
S54.
Número total de alumnos: x. Homes + mulleres = x, polo tanto:
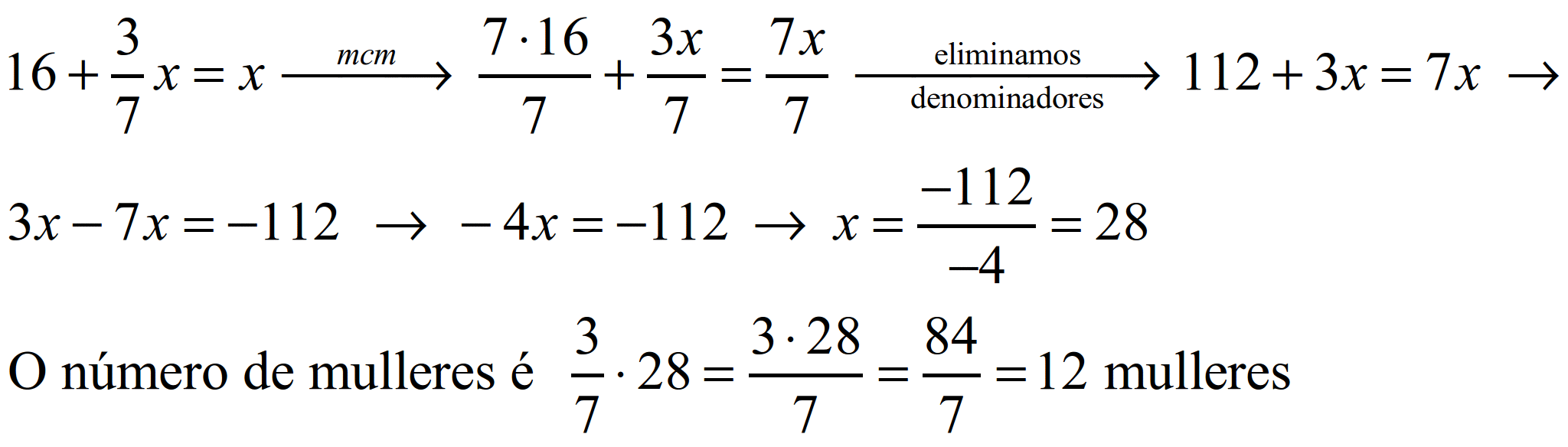
S55.
Lonxitude completa da viaxe = x
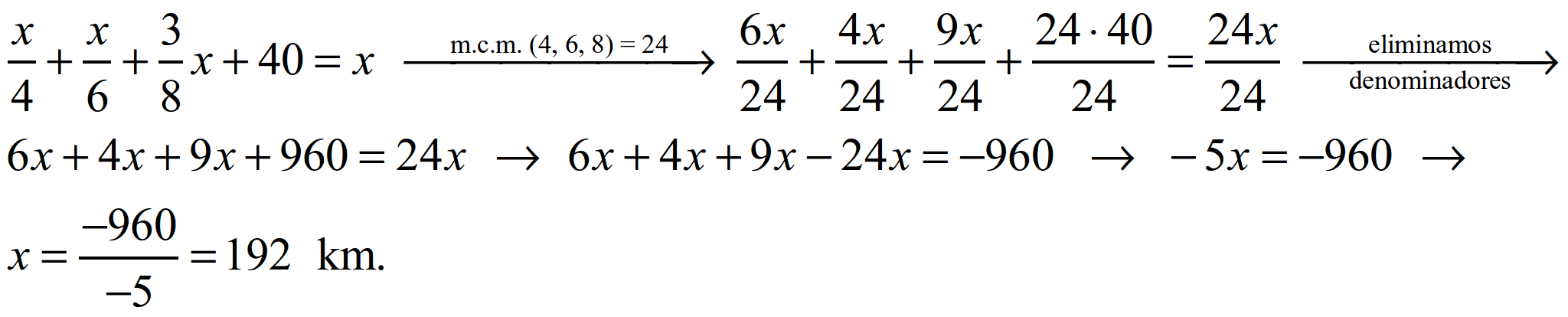
S56.
Custo dunha camisa: x; custo dun pantalón: 1,5x.
Dous pantalóns máis 3 camisas = 195 euros;
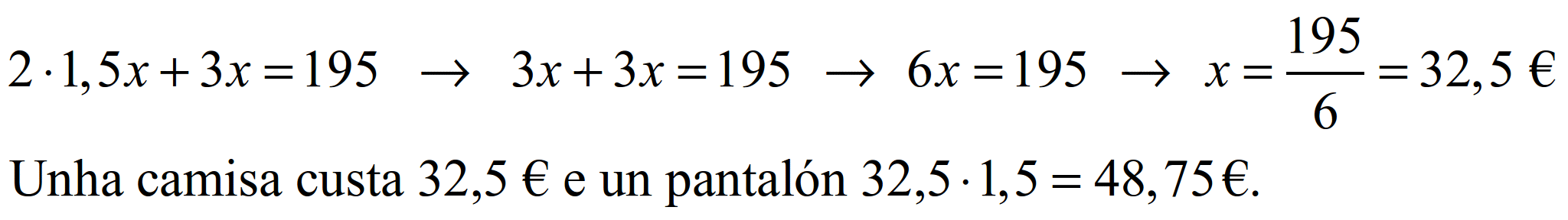
S57.
Número de euros que recibe a terceira persoa: x
Número de euros que recibe a segunda persoa: 2x
Número de euros que recibe a primeira persoa: 3 ·(2x) = 6x
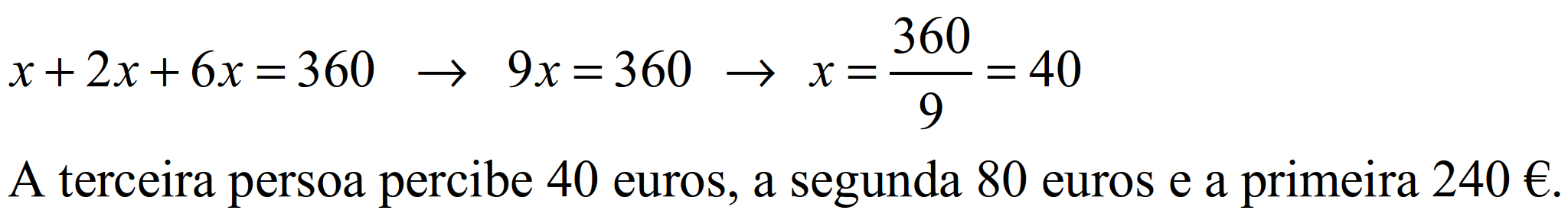
S58.
|
Días |
Quilómetros percorridos |
|
1º |
X |
|
2º |
X+1 |
|
3º |
X+1+1 =X+2 |
|
4º |
X+3 |
|
5º |
X+4 |
|
6º |
X+5 |
|
7º |
X+6 |
|
Total |
42 |
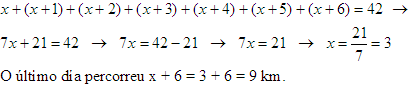
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0