3.2.3 Resolución de problemas con ecuacións de primeiro grao
Na resolución de problemas mediante ecuacións de primeiro grao convén que siga estes pasos:
-
Lea o problema detidamente e identificando o que se pregunta (o que se quere saber); se non entende algunha palabra busque o significado nun dicionario ou en páxinas web.
-
Póñalle un nome (x, por exemplo) á incógnita do problema (unha idade, un número, un tempo, o prezo dalgún obxecto…).
-
Traduza a linguaxe alxébrica a información do problema, escribindo unha ecuación.
-
Resolva a ecuación.
-
Comprobe que o resultado obtido sexa válido e a solución do problema.
Exemplo: se dos euros que teño gasto a metade e lle engado a décima parte dos que tiña ao principio, quédanme 480 euros. Cantos euros tiña inicialmente?
-
[1] A incógnita do problema é os euros que eu tiña ao comezo; chamámoslle x a estes cartos.
-
Euros que tiña inicialmente: x
-
Gastei a metade do que tiña:
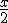
-
Engado a décima parte do que tiña ao principio:
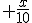
-
[2] Escribimos en linguaxe alxébrica a información subministrada polo enunciado:
Cartos que tiña - cartos que gastei + engadir décima parte = cartos que me quedan:
![]()
-
[3] Resolvemos a ecuación:
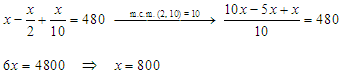
A solución é que tiña inicialmente 800 euros. Agora comprobamos que esta sexa a solución do problema: se gasto a metade quédanme 400 euros, e se lle engado a décima parte de 800 euros, que son 80 euros, daquela quedaranme 480 euros; a solución é correcta.
No caso de que teña que resolver un problema sobre figuras xeométricas, é moi conveniente que faga un debuxo destas, sinalando nel a información que se proporcione (lonxitude dos lados, alturas, perímetros, diámetros, ángulos…).
Una nai ten 64 anos de idade e a súa filla 32. Cantos anos pasaron desde que a idade da nai era o triplo da idade da filla?
|
Solución |
A incógnita é: x = anos que pasaron. Idade da nai hai x anos: 64 – x; idade da filla = 32 – x. A ecuación que hai que escribir corresponde a: Idade da nai hai x anos = 3 veces a idade da filla hai x anos; traducimos isto a linguaxe alxébrica: 64 – x = 3 (32 – x). Resolvemos a ecuación: 64 – x = 96 – 3x → - x + 3x = 96 – 64 → 2x = 32 → x = 16. Hai 16 anos a idade da nai era o triplo da idade da filla; pode comprobalo? |
Un pai ten 35 anos e o seu fillo 5. Dentro de cantos anos a idade do pai será catro veces maior que a idade do fillo?
|
Solución |
Incógnita: x = anos que teñen que pasar. Ecuación que hai que escribir: idade do pai dentro de x anos = 4 multiplicado pola idade do fillo hai x anos; 35 + x = 4 (5 + x) → 35 + x = 20 + 4x → x – 4x = 20 – 35 → -3x = -15 → x = -15/-3 = 5 Dentro de 5 anos o pai terá 40 anos e o fillo 10 anos, daquela a idade do pai será catro veces maior que a do fillo; a solución é correcta. |
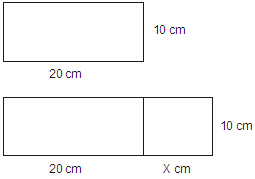
A base dun rectángulo mide 20 cm e a altura 10 cm. Cantos centímetros debe aumentar a base para que a área aumente en 100 cm2?
|
Solución |
|
Chamámoslle x ao que debe aumentar a base do rectángulo. A área do rectángulo inicial é 200 cm2. A área do novo rectángulo é (20 + x).10, e isto ten que dar 200 + 100 = 300 cm2 ; así que escribimos a ecuación: (20+x)10 = 300 Resolvendo a ecuación, resulta x = 10 cm. |
Temos 15 moedas, unhas de 20 céntimos e outras de 50 céntimos. Cantas moedas temos de cada clase se en total son 6 euros?
A incógnita é x = número de moedas de 20 céntimos. Xa que logo, 15 – x é o número de moedas de 50 céntimos. Lembre que 20 céntimos = 0,20 euros e que 50 céntimos = 0,50 euros, así traballamos todo en euros. A ecuación que temos que escribir é, simplemente: cartos totais = 5 euros. Traducimos isto a linguaxe alxébrica:
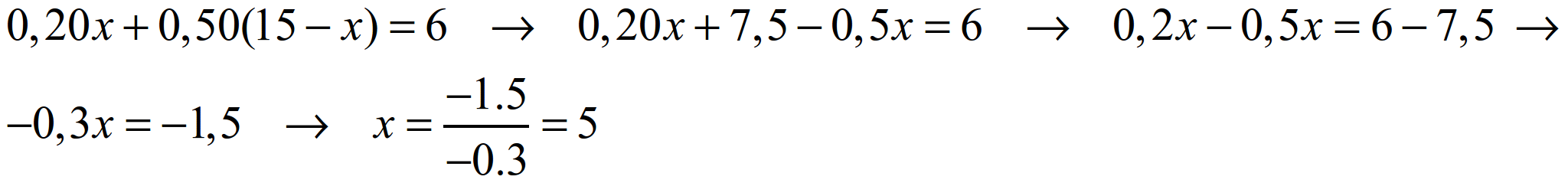
Temos cinco moedas de 20 céntimos e dez de 50 céntimos, o cal efectivamente fai seis euros.
O lado dun cadrado é tres metros maior que o dobre do lado doutro cadrado. Se o perímetro do primeiro cadrado é 48 metros maior que o do segundo, cal é a lonxitude dos lados de ambos os cadrados? (Faga un debuxo cos dous cadrados e escriba neles a información subministrada polo texto do exercicio).
|
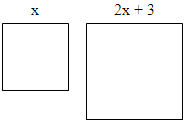
Sexa x a lonxitude do lado do cadrado pequeno. Daquela a lonxitude do lado do cadrado grande é 2x + 3. O perímetro do cadrado grande é 4(2x + 3) = 8x + 12, entanto que o perímetro do cadrado pequeno é 4x. Escribimos a ecuación: Perímetro grande = perímetro pequeno + 48 |
 |
![]()
Comprobamos o resultado. O lado pequeno mide 9, o lado grande mide 2 . 9 + 3 = 21; perímetro do cadrado pequeno = 36; perímetro do cadrado grande = 84; efectivamente cúmprese que 84 é igual a 36 + 48.
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0