Saltar la navegación

De cántaras a cubos

Manejando el fuego

Ahumado de vasija con fuego

Don Xulián intentaba leer las unidades de medida que estaban escritas en el plano, pero no estaban muy claras.

—A ver si entendéis lo que pone aquí —comentó. 

—Está borroso —dijo Uxía— parece que habla de pies, no tiene mucho sentido.

—Antiguamente, algunas medidas de objetos se identificaban con la herramienta que se usaba para medirlos: dedos, manos... —dijo don Xulián—. En el caso de líquidos era común usar el nombre del recipiente, por eso a veces se confundía la vasija con su contenido. Por ejemplo, en Galicia usaban la cántara, que equivalía a 16 litros. Las hacían en las olerías, y también usaban el fuego como los primeros faros.

Demuestra tu capacidad

Muchas personas confunden los conceptos de volumen y capacidad. El primero informa sobre el espacio que ocupa un cuerpo y el segundo sobre la cantidad que cabe dentro de él.

¿Te parece lo mismo? ¿No lo tienes claro? Mira este vídeo y lo entenderás mejor.

¿Cómo interpretas el siguiente applet? ¿Capacidad o volumen?

https://www.geogebra.org/m/tu8gxfcn (Ventana nueva)

Proxecto%20cREAgal,https%3A//www.geogebra.org/m/tu8gxfcn,GG_MAT2ESO_REA08_Cilindro%20Agua,1,Autor%EDa
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

Volumen del cilindro

El principio de Cavalieri establece que, si dos sólidos tienen la misma altura y las áreas de todos los cortes paralelos a sus bases son iguales, entonces sus volúmenes también serán iguales, sin importar la forma de sus bases.

En este caso, el cilindro y el prisma tienen la misma altura y bases con el mismo área, por tanto:

Volumen cilindro = Área base · altura

Fórmula

Volumen cilindro = Área base ⋅ altura = π r2 h 

En el siguiente applet puedes explorar esta relación.

Mueve el deslizador para modificar el número de cortes y observa cómo las áreas de los cortes coinciden en ambos sólidos, verificando el principio de Cavalieri.

https://www.geogebra.org/m/ucsuzvkt (Ventana nueva)

Proxecto%20cREAgal,https%3A//www.geogebra.org/m/ucsuzvkt,GG_MAT2ESO_REA08_Volumen%20Cilindro-%20Principio%20de%20Cavalieri,1,Autor%EDa
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

Ducha de agua caliente

El antiguo Faro de Illa Pancha, ahora un alojamiento turístico, cuenta con un depósito cilíndrico para suministrar agua caliente. Queremos calcular el volumen del depósito para asegurarnos que tienen suficiente capacidad para cubrir las necesidades de los huéspedes.

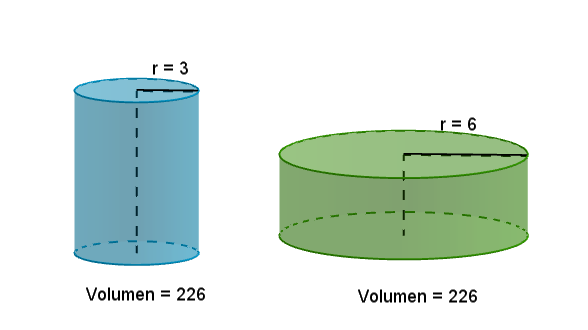
Depósito de aguaDatos del depósito:

  • Altura: 2 metros.
  • Radio de la base: 0,5 metros.
  1. Calcula el volumen del depósito, en metros cúbicos.
  2. Convierte el volumen a litros (1 metro cúbico = 1000 litros).
  3. Si una ducha consume aproximadamente 50 litros de agua caliente, calcula cuántas duchas consecutivas puede abastecer este depósito.

Desafío con cilindros: volúmenes y alturas

Escoge el nivel de dificultad y pon a prueba tus habilidades.

Opción A. Desafío del volumen

Calcula el volumen de los siguientes cilindros ayudándote de los datos que se dan en el applet. Aproxima el resultado a las centésimas.

Cada respuesta correcta suma 2.5 puntos. La puntuación máxima es 10.

https://www.geogebra.org/m/gjsumehn (Ventana nueva)

(Guardar la puntuación)
Proxecto%20cREAgal,https%3A//www.geogebra.org/m/gjsumehn,GG_MAT2ESO_REA08_Volumen%20cilindro%20,1,Autor%EDa
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

Opción B. Descubre la altura

Se quiere construir dos cilindros con el mismo volumen. El primero tiene un radio de 3 cm y el segundo un radio de 6 cm.

Ambos cilindros tienen un volumen total de 226 cm³.

Dos cilindros de los que se conoce el volumen y altura

  • Calcula la altura de cada cilindro.
  • ¿Qué relación observas entre el radio y la altura en estos dos cilindros?

Opción C. Ajusta el cilindro

En el siguiente applet hay dos cilindros:

  • Cilindro fijo (azul): su volumen es constante.
  • Cilindro móvil (verde): puedes modificar su altura desplazando el punto en la vertical.

Cambia la altura del cilindro verde e intenta hacer que su volumen coincida con el del cilindro azul. 

https://www.geogebra.org/m/wpftfqhb (Ventana nueva)

(Guardar la puntuación)
Proxecto%20cREAgal,https%3A//www.geogebra.org/m/wpftfqhb,GG_MAT2ESO_REA08_Vol%FAmenes%20iguales,1,Autor%EDa
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

Creado con eXeLearning (Ventana nueva)