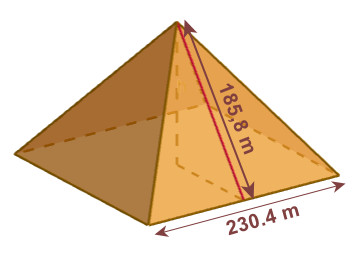
Faro de Alejandría
—¿Sabéis cuál fue el primer faro del que se tiene constancia? —preguntó el farero.
—¿La Torre de Hércules? —se aventuró Uxía.
Don Xulián no pudo evitar esbozar una sonrisa.
—Buen intento, pero no. Fue un faro que doblaba la altura de la Torre de Hércules y que se construyó en el siglo III a.C. Se trata del Faro de Alejandría, en la isla de Pharos, en Egipto.
—¡El siglo III a.C.! —exclamó Uxía sorprendida— ¿Pero cómo podían construir tan alto en aquella época?
—Pues os diré algo más sorprendente todavía. Las pirámides de Guiza fueron construidas más de dos mil años antes, siendo nuevamente un reflejo de los conocimientos arquitectónicos únicos que se tenían en aquella época.
—Entonces, los faros y las pirámides no son solo obras colosales —concluyó Uxía, fascinada.
—Exacto —asintió don Xulián—. Son, además, claros ejemplos de cómo las matemáticas y la creatividad perduran a través del tiempo.
¿Te atreves a descubrir más sobre las pirámides?
Lectura facilitada
—¿Sabéis cuál fue el primer faro que existió? —preguntó don Xulián.
—¿La Torre de Hércules? —dijo Uxía con curiosidad.
Don Xulián sonrió.
—Buen intento, pero no. El primer faro conocido fue el Faro de Alejandría, en Egipto, construido en el siglo III a.C. ¡Era el doble de alto que la Torre de Hércules! Estaba en la isla de Pharos.
—¡El siglo III a.C.! —exclamó Uxía sorprendida— ¿Cómo podían construir algo tan alto en esa época?
—Pues las pirámides de Guiza son aún más antiguas. Fueron construidas más de dos mil años antes y demuestran el gran conocimiento arquitectónico que tenían —explicó don Xulián.
—Entonces, el faro de Alejandría y las pirámides no son solo obras gigantescas —dijo Uxía, admirada.
—Exacto —afirmó don Xulián—. Son ejemplos de cómo las matemáticas y la creatividad han perdurado a lo largo de la historia.
¿Te atreves a descubrir más sobre las pirámides?
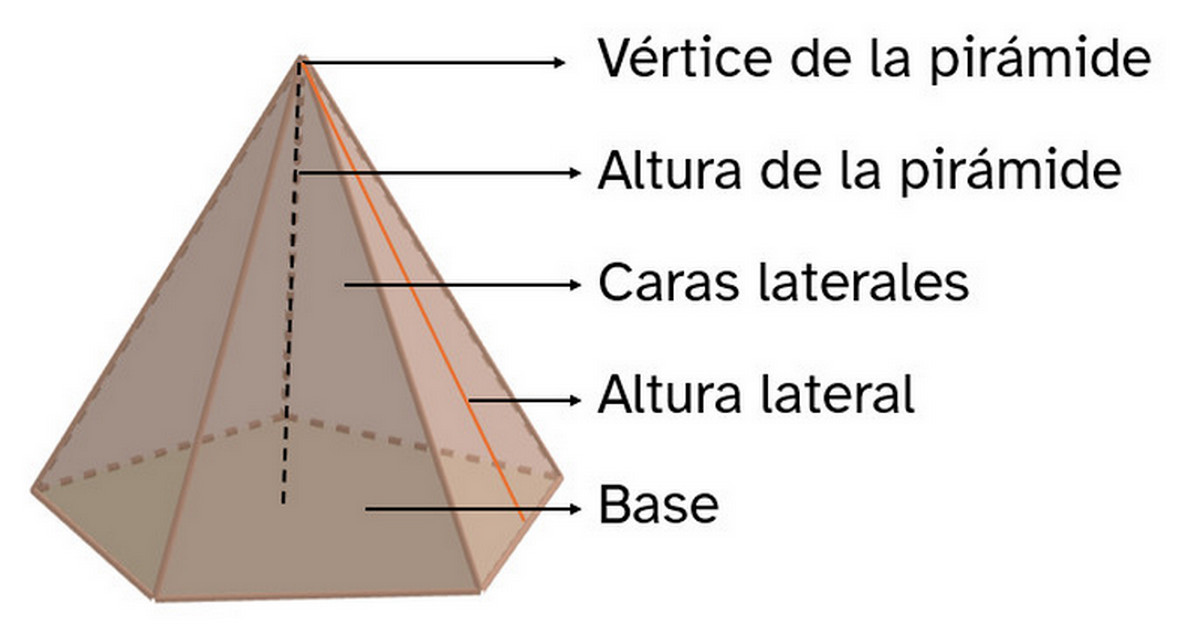
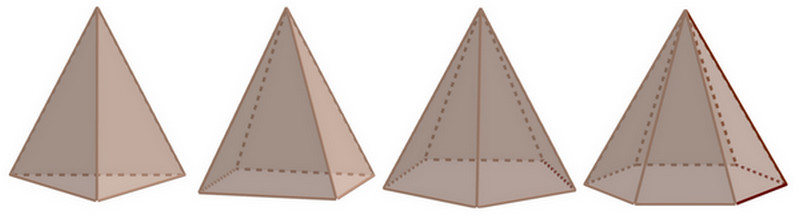
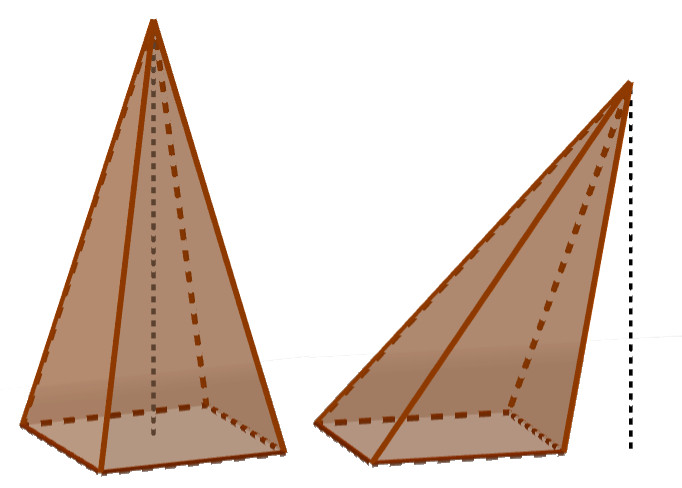
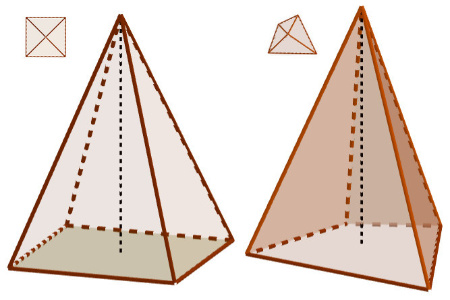
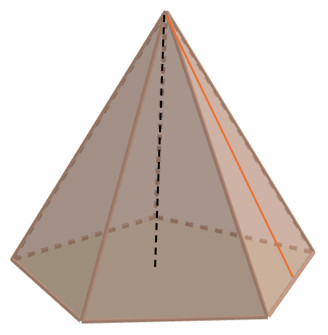Una pirámide es un poliedro que:
