El faro de Cabo Vilán

Después de conocer el museo y las interesantes salas que alberga el Faro de Cabo Vilán, es el momento de poner el foco en su arquitectura.
Tal y como podemos observar en la imagen, el Faro de Cabo Vilán está compuesto por un edificio principal, una majestuosa torre y el túnel que los une.
Vamos a calcular el área de la fachada del edificio, el área de la planta de la torre y la longitud del túnel que conecta ambas estructuras para ayudar al equipo de restauración en sus tareas de conservación del faro.


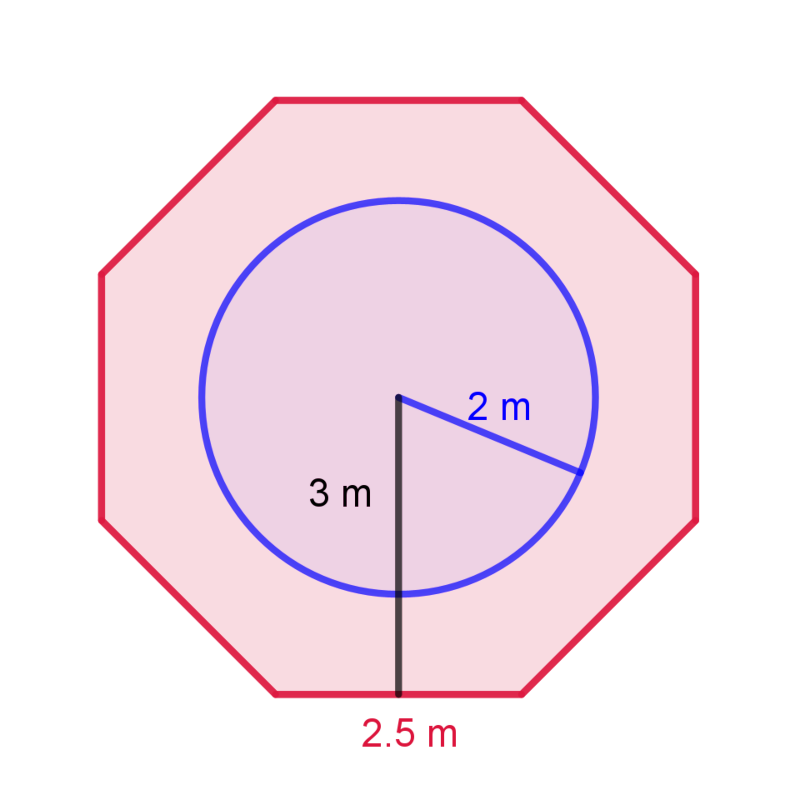

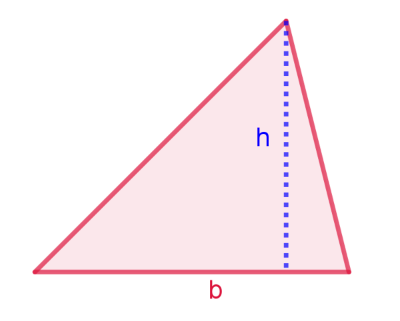

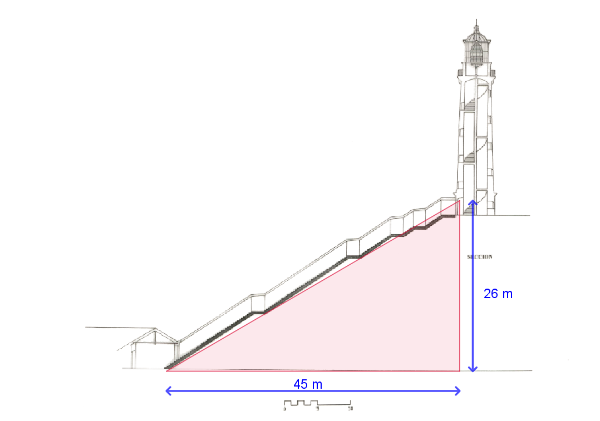


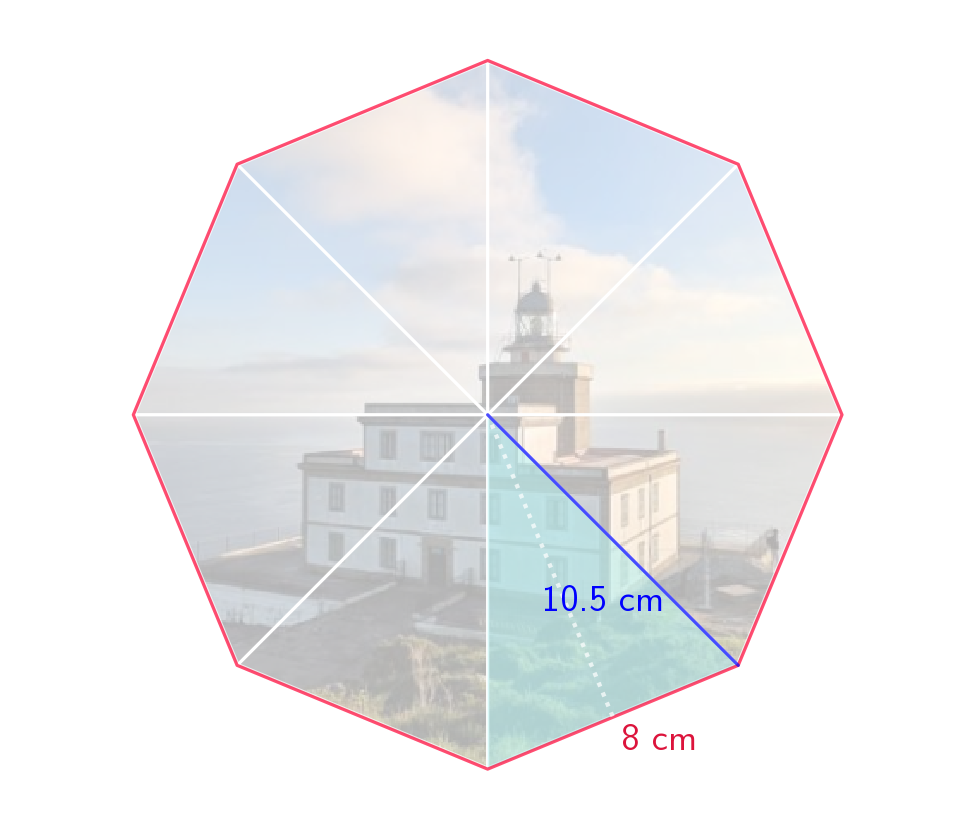


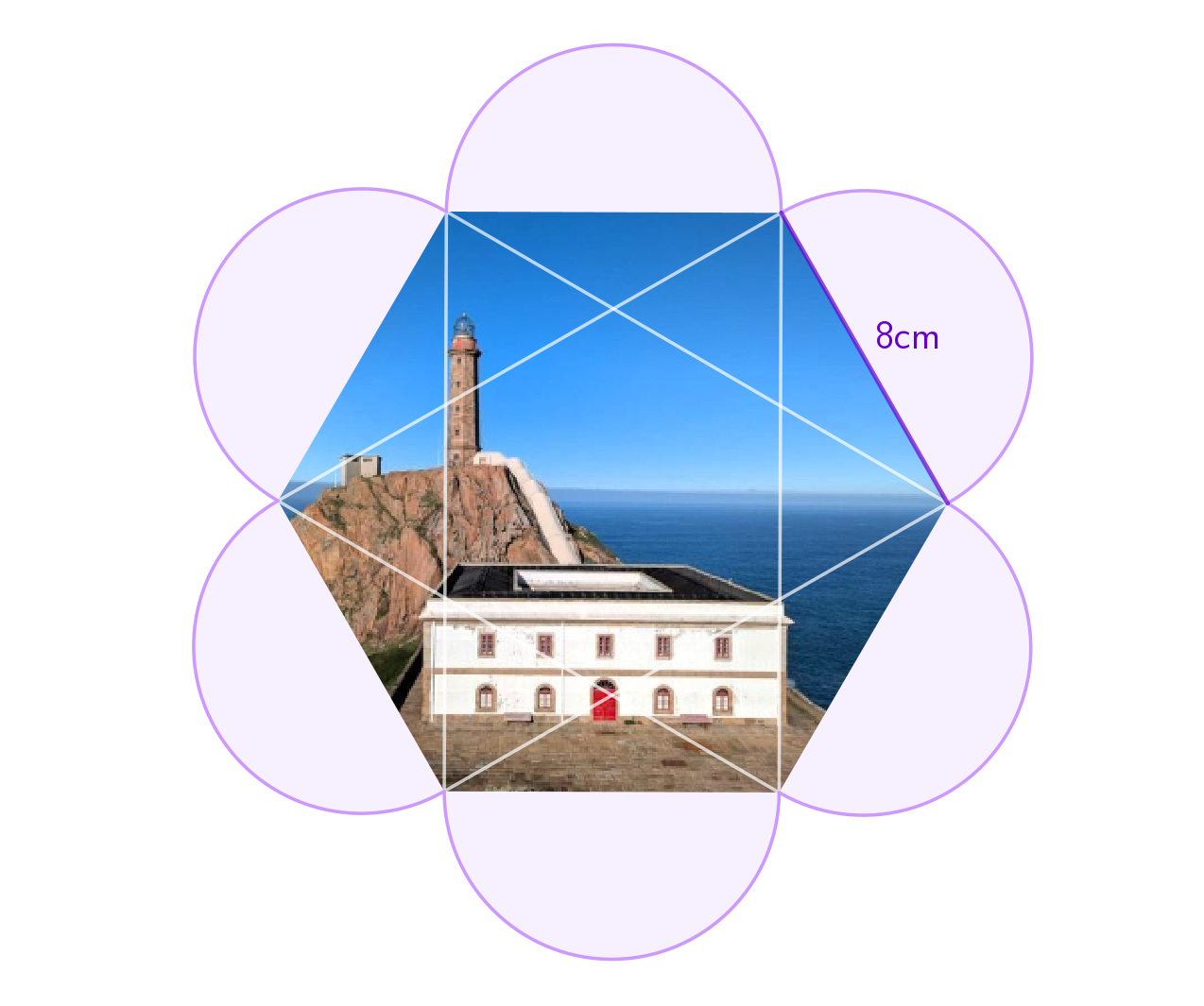
 En la fase 2, se hace un repaso de las figuras planas y del cálculo de sus perímetros y áreas. También se recuerdan los cuerpos geométricos y se identifica su existencia en las diferentes partes de los faros.
En la fase 2, se hace un repaso de las figuras planas y del cálculo de sus perímetros y áreas. También se recuerdan los cuerpos geométricos y se identifica su existencia en las diferentes partes de los faros.