Saltar la navegación

Cubicando

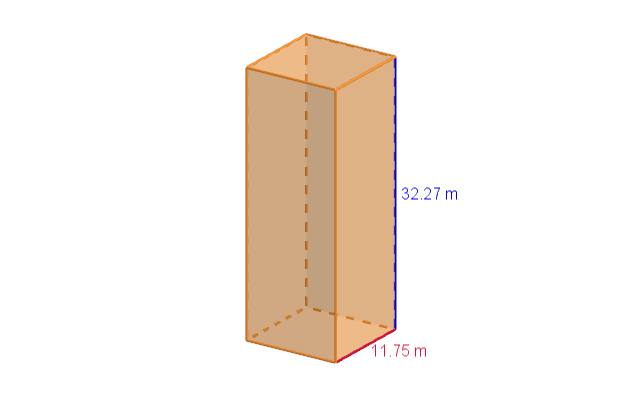
Cubicando la Torre de Hércules

https://www.geogebra.org/m/rt59g6wq (Ventana nueva)

Proxecto%20cREAgal,https%3A//www.geogebra.org/m/rt59g6wq,GG_MAT2ESO_REA08_Torre%20de%20H%E9rcules,1,Autor%EDa
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

Uxía y su equipo observaban planos y cálculos dispersos por la mesa cuando Don Xulián preguntó:

—Antes de construir, ¿cómo calculamos los materiales?

—¿Midiendo? —dudó Uxía.

—Se llama cubicar —explicó el farero que ante las caras de sorpresa prosiguió—. Es decir, hay que calcular dimensiones y materiales según las formas geométricas. De ahí la importancia de analizarlas bien.

Iniciación al volumen

A continuación, se muestran dos prismas formados por 4 cubos unitarios, pero organizados de formas diferentes. 

Cubos apilados

    Preguntas:

    • ¿Cuál es el área de cada uno de los prismas?
    • ¿Y el volumen de cada uno?

    Reflexión

    A pesar de que los dos prismas tienen una forma diferente, su volumen es el mismo porque ambos están formados por el mismo número de cubos.

    Definición

    El volumen de un cuerpo es la medida de la cantidad de espacio que ocupa.

    Para medirlo, utilizamos unidades cúbicas. La unidad principal es el metro cúbico (m³), que representa el volumen de un cubo de 1 metro de arista.

    En general, utilizamos múltiplos y submúltiplos de estas unidades para medir el volumen de objetos más grandes o más pequeños.

    Volumen de un ortoedro

    En el siguiente applet tienes un ortoedro formado por cubos de 1 unidad cúbica (1 u³). 

    Instrucciones:

    • Ajusta los deslizadores para cambiar el largo, el ancho y la altura del prisma.
    • Observa cómo varía el número total de cubos a medida que modificas estas dimensiones.

    Preguntas:

    1. ¿Cómo cambia el volumen cuando aumentas la altura del prisma?
    2. Si cambias el largo y el ancho del prisma, ¿cómo afecta esto al volumen?
    3. ¿Cómo puedes calcular el volumen del prisma sin contar los cubos uno a uno?
    4. ¿Qué relación encuentras entre las dimensiones (largo, ancho, altura) y el volumen del prisma?

    https://www.geogebra.org/m/gmjmefvs (Ventana nueva)

    Proxecto%20cREAgal,https%3A//www.geogebra.org/m/gmjmefvs,GG_MAT2ESO_REA08_Contando_cubos,1,Autor%EDa
    Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

    Fórmula

    Para calcular el volumen de un prisma rectangular, podemos contar cuántos cubos de 1 u³ caben dentro de él.

    Si llamamos
    a    ,
    b     y
    c     al número de cubos que caben a lo largo, a lo ancho y a lo alto del prisma, el número total de cubos se obtiene multiplicando a \cdot b \cdot c.

    Por lo tanto, la fórmula del volumen de un prisma rectangular recto es:

    Donde , y c son las dimensiones del prisma (largo, ancho y altura).

    Practica volumen de ortoedros

    Calcula el volumen de los siguientes ortoedros.

    Cada respuesta correcta suma 2 puntos y cada fallo resta 1 punto. La puntuación máxima es 10.

    https://www.geogebra.org/m/rybymevj (Ventana nueva)

    (Guardar la puntuación)
    Proxecto%20cREAgal,https%3A//www.geogebra.org/m/rybymevj,GG_MAT2ESO_REA08%20Volumen%20de%20prisma-autoevaluable,1,Autor%EDa
    Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

    Practica volumen de ortoedros combinados

    En esta actividad interactiva, tendrás que calcular el volumen de figuras tridimensionales formadas por la combinación de dos prismas rectangulares.

    • Determina y anota la longitud, anchura y altura de cada prisma que compone la figura.
    • Calcula el volumen de cada prisma.
    • Obtén el volumen total.


    Preguntas para reflexionar

    • ¿Se te ocurre otra forma de descomponer o componer la figura diferente a la que pensaste inicialmente?
    • ¿El volumen de la figura será diferente según cómo la hayas descompuesto? ¿Por qué?

    https://www.geogebra.org/m/j3tvsxnz (Ventana nueva)

    (Guardar la puntuación)
    Proxecto%20cREAgal,https%3A//www.geogebra.org/m/j3tvsxnz,GG_MAT2ESO_REA08_Volumen%20de%20Figuras%20compuestas,1,Autor%EDa
    Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

    Volumen de un prisma

    En el siguiente applet se muestran dos representaciones de un prisma:

    • El prisma completo, cortado en secciones (rebanadas) horizontales.
    • Las mismas rebanadas, desplazadas horizontalmente para formar una figura distinta.

    https://www.geogebra.org/m/vhncxtdj (Ventana nueva)

    Proxecto%20cREAgal,https%3A//www.geogebra.org/m/vhncxtdj,GG_MAT2ESO_REA08_Principio%20de%20Cavalieri_Ortoedro,1,Autor%EDa
    Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

    Preguntas: 

    1. ¿Qué puedes decir sobre las rebanadas de las dos figuras? ¿Son iguales en tamaño y forma? 
    2. ¿Tienen las figuras la misma altura total? 
    3. Si las rebanadas tienen el mismo área y altura, ¿el volumen total será el mismo o diferente? ¿Por qué? 
    4. ¿Importa cómo están organizadas las rebanadas para determinar el volumen?

    Principio de Cavalieri

    Si dos figuras tienen:

    • La misma altura.
    • Y las secciones paralelas a la base (rebanadas) tienen igual área.

    Entonces, los volúmenes de ambas figuras serán iguales, sin importar cómo estén organizadas las secciones ni su forma.

    Fórmula del volumen de un prisma

    Utilizando el principio de Cavalieri, deducimos la fórmula general para calcular el volumen de un prisma:

    Volumen del prisma = Área de la base · Altura del prisma

    Practica volumen de prismas regulares

    Calcula el volumen de los siguientes prismas ayudándote de los datos que se dan en el applet. Aproxima el resultado a las centésimas.

    Cada respuesta correcta suma 2.5 puntos. La puntuación máxima es 10.

    https://www.geogebra.org/m/ahxt2geu (Ventana nueva)

    (Guardar la puntuación)
    Proxecto%20cREAgal,https%3A//www.geogebra.org/m/ahxt2geu,GG_MAT2ESO_REA08_Volumen%20prisma%20regular%20-autoevaluable,1,Autor%EDa
    Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

    El volumen de la Torre de Hércules

    Imagina que la torre necesita instalar un nuevo sistema de ventilación para mejorar la comodidad de los visitantes y proteger la estructura de la humedad.

    Para diseñar este sistema, necesitamos calcular el volumen de dos partes principales de la Torre de Hércules:

    • La torre cuadrangular (base del faro).
    • La sección octogonal situada debajo de la linterna.

    Ignoraremos las escaleras y divisiones internas para simplificar el cálculo.

    Plano de la Torre de Hércules
    Galiciana. Plano de la Torre de Hércules (CC BY-NC-ND)

    1. La torre cuadrangular

    La base del faro es un prisma cuadrangular con las siguientes medidas:

    • Lado del cuadrado: 11,75 m.
    • Altura del prisma: 32,37 m.
    Prisma cuadrangular

    2. La linterna

    La sección situada debajo de la lámpara del faro es un prisma octogonal con las siguientes medidas:

    • Lado del octógono: 1,9 m.
    • Radio del octógono: 2,5 m.
    • Altura del prisma: 4,5 m.
    Prisma octogonal

    Creado con eXeLearning (Ventana nueva)