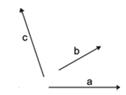
2.1.4 Suma de forzas (suma de vectores)
Sumar números é moi doado, pero... e sumar vectores? Con números, 2 + 2 dá sempre 4, pero con vectores a operación 2 + 2 pode dar calquera resultado entre 0 e 4. Isto é así porque na suma de vectores hai que ter en conta tamén a súa dirección e o seu sentido.
Suma de vectores con igual dirección
Empecemos polo máis sinxelo. Fíxese nos debuxos e aprenda a calcular a suma:
-
Sumar os vectores…
Vector resultante

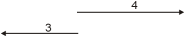
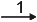
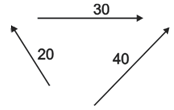
O sentido do vector resultante é o sentido do maior dos dous vectores que se suman.
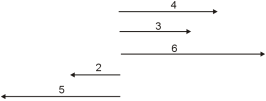
Sumamos os vectores que teñen sentido cara á dereita, e dá 13; sumamos os que van cara á esquerda, que dan 7, e logo sumamos como no caso anterior.
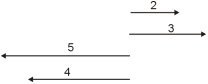

Un vector de módulo 5 cara a dereita máis un de módulo 9 cara a esquerda dá como resultado outro vector de módulo 4 á esquerda.
Xa ve que a suma de vectores que teñen igual dirección dá outro vector que ten a mesma dirección que eles; o sentido depende dos módulos dos sumandos.
Sumar vectores que teñen distinta dirección é algo máis complicado. Imos ver dous métodos gráficos para sumalos: o método do paralelogramo e o método do polígono.
Suma de vectores polo método do paralelogramo
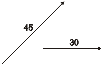
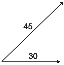
Supoña que queremos sumar dous vectores de módulos 45 e 30 que forman ángulo entre eles. Fíxese como se fai por este método do paralelogramo coa secuencia de pasos que se indican:
-
-
1º. Movemos os vectores ata xuntar as súas orixes (sen xiralos nin cambiar o seu tamaño)
Resultado
-
-
-
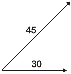
2º. Debuxamos liñas auxiliares paralelas aos vectores
Resultado

-
-
-
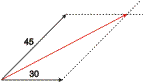
3º. Debuxamos o vector resultante da suma
Resultado

-
O vector resultante da suma é outro vector cunha dirección diferente. Canto vale o seu módulo? Hai unha fórmula matemática que permite sabelo, pero é algo complicada; outro xeito de sabelo é debuxarmos os vectores a escala e medirmos cunha regra a lonxitude do vector resultante. No caso da figura, o módulo do resultado é 69,5. Compróbeo vostede mesmo.
Suma de vectores polo método do polígono
É un método útil cando hai que sumar máis de dous vectores con distintas direccións. Hai que ir pondo a orixe dun vector deseguido do extremo (o final) do vector anterior; o vector resultante é o que vai desde a orixe do primeiro ata o extremo do último que colocamos.
Vexámolo cun exemplo. Queremos sumar os vectores seguintes:
Collemos un vector calquera dos tres e desprazámolo para un novo debuxo. Logo imos engadindo os demais. Fíxese ben como é o proceso:
-
-
1º. Collemos un vector calquera, por exemplo o c.
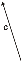
-
-
-
2º. No extremo do vector c colocamos outro vector, por exemplo o vector a.
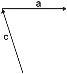
-
-
-
3º. Engadimos o vector que falta do mesmo xeito.
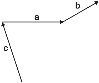
-
-
-
4º. O vector resultante é o vector que vai desde a orixe do primeiro ata o extremo do último.
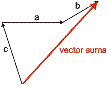
-
Para sabermos o módulo do vector resultante por este método do polígono, temos que facer o debuxo a escala e medir a lonxitude do vector suma.
No caso especial, e frecuente, de termos que sumar dous vectores perpendiculares, podemos calcular o módulo do vector suma usando o teorema de Pitágoras:
-
Vectores para sumar
Trazamos liñas auxiliares
Vector resultante
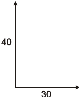
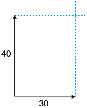
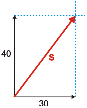
O módulo do vector da suma anterior é:
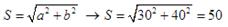
Actividades resoltas
Sume polo método do paralelogramo os vectores que se indican, mediante un debuxo a escala medindo o módulo do vector resultante da suma:
-
Vectores
Resultado
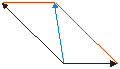
O módulo do vector resultante sabémolo medindo a lonxitude do vector suma (azul na figura). Debe darlle un módulo de 17,9 aproximadamente.
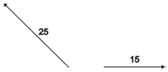
Calcule a suma de dúas forzas perpendiculares, unha de 25 N e outra de 44 N. Debuxe os vectores e o vector suma.
-
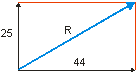
O módulo do vector suma calculámolo usando o teorema de Pitágoras:
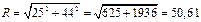
Actividades propostas
S2. Debuxe e calcule o módulo do vector resultante de sumar os vectores seguintes:
- Un de módulo 4, vertical cara a arriba máis un de módulo 3 vertical cara a arriba e máis outro de módulo 9 vertical e sentido cara a abaixo.
- Tres vectores inclinados 45º, de módulos 3, 6 e 1 respectivamente, os dous primeiros dirixidos cara á dereita e o terceiro dirixido cara á esquerda.
S3. Sume as forzas polo método do polígono; logo mida o módulo da forza resultante.
S4. O resultado de sumar dúas forzas perpendiculares é un vector de módulo 53,85 N. Se unha das forzas que se sumou vale 20 N, canto vale a outra forza?
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0