2.1.3 A forza é unha magnitude vectorial
As magnitudes pódense clasificar en escalares e vectoriais.
Magnitudes escalares
Son as que quedan totalmente determinadas (coñecidas) sabendo o seu valor numérico e a súa unidade.
Daquela, a masa é unha magnitude escalar, porque se dun corpo sabemos que ten 30 kg (número e unidade) xa sabemos todo o que hai que saber da súa masa; o volume tamén é unha magnitude escalar: se sabemos que un bloque de granito ten 2 m3 (número e unidade) o seu volume está perfectamente coñecido.
O mesmo pasa coa magnitude tempo: se dicimos que unha película dura 1,60 h (número e unidade), do tempo non hai máis nada que saber.
Magnitudes vectoriais
Son as magnitudes que, para coñecérmolas totalmente, cómpre sabermos ademais a súa dirección e o seu sentido. Un exemplo doado de magnitude vectorial é a velocidade. Se nos din que un coche está nun cruce de estradas e que se move a 60 km/h, non o sabemos todo da súa velocidade: falta coñecermos en que dirección se move e en que sentido:
Se dicimos que un corpo se move a 30 m/s, dirección vertical e sentido cara a arriba, daquela si sabemos todo sobre a súa velocidade.
-
-
Vectores. As magnitudes vectoriais represéntanse na escritura con vectores. Un vector é unha porción de recta (un segmento) orientado; isto é, que ten unha orientación definida.
-
- Elementos dos vectores:
– Módulo: é o valor numérico do vector. Exemplo: 35 N; 22 m/s. O módulo dun vector sempre é un número positivo.
– Dirección: é a dirección da recta sobre a que está debuxado o vector. Podemos dar a dirección cun ángulo; así podemos dicir que a velocidade dun avión está inclinada 30º respecto da horizontal. En navegación a dirección tamén se indica cos puntos cardinais (suroeste, nordeste, etc.)
– Sentido: dentro de cada dirección pode haber dous sentidos, cara a un lado ou cara ao contrario. No exemplo do avión anterior, o sentido podería ser cara a arriba (o avión vai subindo) ou cara a abaixo (vai baixando).
– Punto de aplicación ou orixe: é o punto de inicio do vector.
Neste enderezo web pode ver máis sobre os elementos dun vector:
Actividade resolta
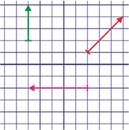
Para cada un dos vectores da figura indique cal é o seu módulo, a súa dirección, o seu sentido e a súa orixe:
-
-
Vector verde: módulo 3, dirección vertical, sentido cara a arriba, orixe no punto (-3, 2).
-
Vector vermello: módulo
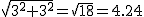, dirección 45º, sentido cara a arriba; orixe no punto (2, 1). -
Vector rosa: módulo 5, dirección horizontal, sentido cara á esquerda, orixe no punto (2, -2).
-
Actividade práctica
As forzas tamén son vectores; ímolo comprobar nesta actividade. Collemos varios dinamómetros e un anel metálico e facemos as seguintes experiencias:
- Colocamos dous dinamómetros como indica a figura, ben aliñados. Comprobamos que ambos indican a mesma forza, dentro do erro experimental de medida e do ben calibrados que estean.
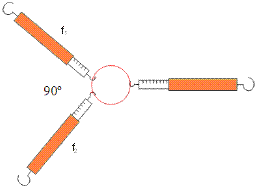
- Con tres dinamómetros medimos a forza que fai cada un deles na situación seguinte:
- Observamos que a suma das forzas dos dinamómetros da esquerda é igual que a forza que marca o da dereita.
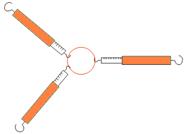
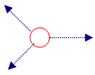
- Colocamos dous dinamómetros en ángulo recto. Como temos que colocar un terceiro para equilibrar o conxunto? Fixámonos no que marcan os tres dinamómetros.
Vemos que a forza que indica o dinamómetro da dereita é igual a 
, é dicir, as forzas súmanse mediante o teorema de Pitágoras neste caso.
Podemos explicar eses resultados aceptando que as forzas se comportan como vectores:
-
Experiencia
Esquema das forzas como vectores
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0