2.4 Operacións con números reais. Representación na recta real
As operacións con números reais son as mesmas que con números racionais. As operacións realízanse con aproximacións decimais, por defecto ou por exceso, con máis ou menos cifras dependendo do grao de precisión que desexemos.
Na práctica utilízanse aproximacións por defecto. As propiedades son as mesmas que cos números racionais.
Raíz dun número
x3 = 27 x = 3
![]() , xa que 33 = 27
, xa que 33 = 27
![]() , xa que 52 = 25 e (-5)2 = 25
, xa que 52 = 25 e (-5)2 = 25 ![]() , xa que 169 =(
, xa que 169 =(![]() 13)2
13)2
![]() , xa que (- 4)3 = - 64
, xa que (- 4)3 = - 64 ![]() , xa que 53 = 125
, xa que 53 = 125
En xeral:
-
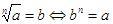
sendo n un número natural, chámase raíz enésima de a en
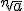
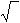 chámase radical .
chámase radical .a chámase radicando.
-
Se n é par a > 0
-
Se n é impar a pode ser calquera número.
-
Se n = 2 raíz cadrada.
-
Se n = 3 raíz cúbica.
-
Se n = 4 raíz cuarta.
-
Exemplo:
![]()
![]()
Operacións con radicais. Propiedades dos radicais
-
Propiedades dos radicais
Lembre
-
As raíces coa calculadora
Tecla
Se a calculadora dispón desta tecla, para achar
, terá que operar do seguinte xeito:
54
4 =
Se a calculadora non dispón desa tecla utilizaremos a tecla
e logo
54
4
=

Representación na recta real. Ordenación de números reais
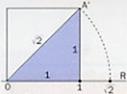
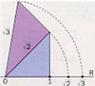
Para representar os irracionais na recta real tomamos regra e compás para calcular o seu valor, polo procedemento do debuxo. Trátase de calcular o valor da hipotenusa dun triángulo de lado 1, e trasladalo co compás á recta real. No segundo caso, de novo temos a hipotenusa dun triangulo rectángulo de lados 1 e ![]() , do que a hipotenusa vale
, do que a hipotenusa vale ![]() , valor que trasladamos de novo á recta real.
, valor que trasladamos de novo á recta real.
Con todo, moitos números non se poden representar por este método, e teremos que utilizar aproximacións decimais, como para representar ![]() , ou para representar
, ou para representar ![]() .
.
Para compararmos números racionais tiñamos que pór as fraccións co mesmo denominador e logo comparar os numeradores, ou ben comparar as súas expresións decimais.
Actividades resoltas
Cal é menor: ![]() ou
ou ![]() ?
?
-
Solución
A resposta non é inmediata; teremos que os reducir a común denominador e logo comparar os numeradores:
mcm (4,7) = 28
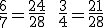
logo termos que
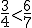
Ou ben pasalos a expresión decimal e logo facer a comparación:
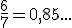
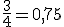
Logo:
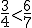
Dados os números irracionais ![]() e
e ![]() , cal é menor?
, cal é menor?
-
Solución
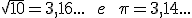
Logo
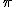 <
< 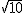
Para comparar números decimais, pásanse previamente forma decimal e logo faise a comparación.
Na recta real, temos que fixar a orixe e as unidades deben ser da mesma medida
Actividades propostas
S14. Ordena os números seguintes: -2; 2; -7; 1,432; 0; 1,43; 4/5; 1,403.
S15. Compare os números 5/6 e 7/8 .
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0