2.2 Porcentaxes

O cálculo de porcentaxes, aumentos e diminucións está ben relacionado coas facturas domésticas. Sabemos que unha porcentaxe é un xeito de expresar un numero cunha fracción de 100: por cento significa cada cen.

% é un xeito de pór os dous ceros, e evolucionou a partir dun símbolo similar, só que coa liña horizontal en lugar de diagonal, que á súa vez provén dun símbolo que representaba P cento.

O uso das porcentaxes podémolo atopar en comisións, descontos, aumentos, impostos e xuros, pero é frecuente errar no seu cálculo, debido ás veces a un mal entendemento do seu uso. Falar dunha subida ou baixada dun 10 % só é comprensible se temos con que comparala. Un erro común no uso das porcentaxes é imaxinar que unha subida do 50 % se cancela cunha baixada da mesma porcentaxe.

Exemplo. Se partimos dunha cantidade fixa como, 100, e lle incrementamos o 50 % e logo dimitiumos o 50 %, como quedaría ao final?

Resultado. Se temos 100 e calculamos o 50 %, teremos 150, pero unha baixada do 50 % de 150 son 75, polo que teremos 75. Así que partimos de 100 e temos agora 75.

Unha porcentaxe é una fracción ou un numero decimal, e tamén un numero decimal ou fracción representa unha porcentaxe.

A expresión decimal dunha fracción resulta ser o tanto por un: 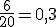( tanto por un)

Se este número se multiplica por 100, teremos o tanto por cen: 0,3 x 100 = 30%