2.3.1 Aproximación decimal dos números irracionais
Un número irracional ten un número ilimitado de cifras; por tanto, o seu valor exacto é imposible de escribir. Para manexármonos con eles termos que utilizar aproximacións.
Vexamos como se calculan as aproximacións decimais de ![]()
Sabemos que ![]()
Aproximación enteira: 1, 2, 3, 4, .....
![]()
logo 3 < ![]() < 4
< 4
O erro cometido é menor que 1 , xa que 4 – 3 = 1
Aproximación decimal: 3,1; 3,2; 3,3; ....
![]()
logo 3,6 < ![]() < 3,7
< 3,7
O erro cometido é menor que 0,1 xa que 3,61 – 3,60 = 0,1
Aproximación centesimal: 3,61; 3,62,....
![]()
logo 3,60 < ![]() < 3,61
< 3,61
O erro cometido é menor que 0,01 xa que 3,61 – 3,60 = 0,01
Seguindo este proceso, obteriamos todas las cifras decimais e escribiriamos
![]() = 3,6055512.......
= 3,6055512.......
Este é un número irracional.
Resumiremos na táboa seguinte este proceso.
-
-
Por exceso
4
3,7
3,61
3,606
...
-
Por defecto
3
3,6
3,60
3,605
...
-
Diferenza
1
0,1
0,01
0,001
...
-
Erro <
1 unidade
1 décima
1 centésima
1 milésima
...
-
-
Historias de
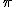
Nun documento exipcio de hai 1 700 anos (o papiro de Rhind) xa se menciona este nuemro e dáselle o valor 256/81, ou o que é o mesmo 3,1604, aínda que non afina moito.
O matematico chinés Tsu Chung-Chih (que viviu hai uns 1 500 anos) deulle o valor de 355/113, é dicir, 3,1415929. Xa se ía achegando.
A idea de designar o número co simbolo é bastante máis recente (hai uns 300 anos) e ocorreuselle ao matematico inglés Willian Jones, aínda que quen popularizou o seu uso foi o suízo Leonard Euler uns cen anos máis tarde.
Ao longo da historia, os matemáticos de todo o mundo trataron de obter maiores aproximacións. Unha das últimas é a que lograron David e Gregory Chudnovsky, da universidade de Columbia, en Nova York (EEUU), que acharon o seu valor con 1 011 196 691 decimais. Se a tivésemos que escribir en folios normais, a cifra obtida ocuparía 260 000 páxinas
Actividade resolta
Escriba un número real comprendido entre:
-
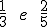
-
0,34
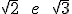
-
1,5
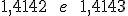
-
1,41425
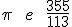
-
3,141517
-
Actividades propostas
S13. Que cantidade de arame cómpre para cercar unha leira cadrada de 2 000 m2 se se queren pór tres voltas de arame? Ache o lado cunha aproximación de centésimas.
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0