2.3 Números irracionais

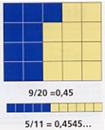
Ata agora vimos que toda fracción ten unha expresión decimal ( exacta ou periódica) e que todo numero decimal exacto ou periódico pódese poñer en forma de fracción.

Pero que sucede no caso seguinte?

Achemos a diagonal do cadrado seguinte, de lado 1.

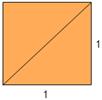
Buscando o valor da diagonal, temos que

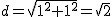
Cando intentamos expresar o valor de , atópamos cunha expresión non coñecida ata agora 1,4142135..., expresión que non podemos transformar nunha fracción.

Atopámonos cun novo tipo de número, que chamaremos irracional e que non podemos expresar como fracción. Estamos ante outro tipo de número, que xunto cos estudados ata agora forman o conxunto dos números reais, R.

Un dos números irracionais máis coñecido e o número , que seguramente asocie á formula da lonxitude dunha circunferencia L = 2··r