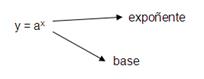
2.4.1 Descrición da función exponencial e a súa gráfica
Analicemos as seguintes situacións:
- Temos unha folla de papel e dobrámola pola metade. Logo realizamos unha nova dobrez e unha máis, ata termos o papel dobrado catro veces. Se este proceso o repetimos 40 veces, canto pensa que tería de grosor? Menos dun metro, entre 1 e 10 metros, máis de 10 metros? Sorprenderíase ao saber que non é posible realizar 40 dobreces, e que o grosor sería suficiente para chegar da Terra á Lúa.
Isto supón un crecemento exponencial, duplicación, reduplicación e de novo duplicación. O noso pensamento é lineal e pensar de xeito exponencial é moi difícil.
- Unha colonia de células de lévedos, na que cada célula se duplica cada 10 minutos, crece de xeito exponencial. Por cada célula, cada 10 minutos, haberá dúas novas células. Despois doutros 10 minutos, haberá catro células, 10 minutos despois haberá oito células e así sucesivamente, a máis células de lévedos, máis células novas haberá cada 10 minutos.
- Unha lenda India conta que un rei lle ofreceu ao inventor do xadrez unha recompensa pola invención de tan entretido xogo, e o Bramán solicitou que lle fose concedido un gran de arroz polo primeiro cadro, dous grans polo segundo, catro polo terceiro e así duplicando a cantidade ata chegar á totalidade dos 64 cadriños que ten o xadrez. O rei accedeu de inmediato, sen caer na conta da cantidade que tiña que sacar das súas arcas, fagamos unha estimación, completando a táboa seguinte:
-
-
Cadriños
1
2
3
4
5
6
7
8
9
10
-
Grans
2
4=22
8=23
16=24
32=25
-
Observemos que polo cadro 10 tería que recibir: 210 = 1 024 grans de arroz,
E polo cadro 30 tería 230 = 1 073 741 824 grans de arroz.
Para sorpresa do rei, foi incapaz de cumprir a promesa, xa que non tiña arroz suficiente no seu reino.
Estamos ante unha función chamada exponencial e ten por expresión:
O caso particular anterior é unha función exponencial de expresión y = 2x, e polo tanto de base 2.
Antes de representar graficamente esta función, debemos saber que:
-
O seu dominio é toda a recta real. Os valores da variable independente (x) que podemos usar.
-
O seu percorrido son o conxunto dos números reais positivos. Os posibles resultados que obtemos (y).
-
A súa gráfica pasa sempre polo punto (0,1).
-
É crecente e continua en todo o seu dominio.
Vexamos a táboa da función y =2x e a súa representación gráfica:
-
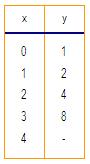
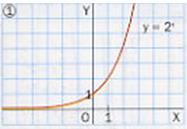
Gráfica da función exponencial y = 2x
Unha cantidade crece exponencialmente cando o seu incremento é proporcional ao que xa existía.
Actividade resolta
Unha persoa ingresa 10 000 euros nun banco ao 7 % anual. Os xuros producidos cada ano acumúlanse ao capital para produciren novos xuros ao ano seguinte, e así sucesivamente.
a) Canto tempo terá que pasar para duplicar o capital que ingresou?
-
Solución
Os xuros producidos ao 7 % anual no primeiro ano son:
10 000·
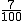 = 10 000 · 0,07 = 700 EUR
= 10 000 · 0,07 = 700 EURAo final do ano terá:
10 000 de capital + 700 de xuros = 10 700 = 10 000 · (1 + 0,07) = 10 000 · 1,07
Fagamos unha táboa:

Vendo a táboa, deducimos que o capital formado en x anos será:
C = 10 000· (1,07)x
Podemos utilizar a calculadora, para buscar o valor de x, e atoparemos que será en 10 anos aproximadamente.
b) Se en lugar de pagar os xuros ao final do ano se pagasen ao final de cada trimestre, canto recibiría en cinco anos?
-
Solución
Se os xuros son trimestrais, teremos que utilizar o valor do xuro dividido entre catro trimestres que ten cada ano
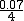
Xa que logo, en cinco anos:
C =
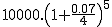 tr= 14 417,78 euros.
tr= 14 417,78 euros.
Actividades propostas
S16. Busque información de situacións que teñan un crecemento exponencial e as gráficas correspondentes. Comprobe que a lectura da gráfica corresponde ao estudo.
S17. Ache a táboa de valores da función exponencial y = 3x, para catro valores da variable x.
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0