2.2.3 Exemplos de funcións

Funcións lineais (y = mx)

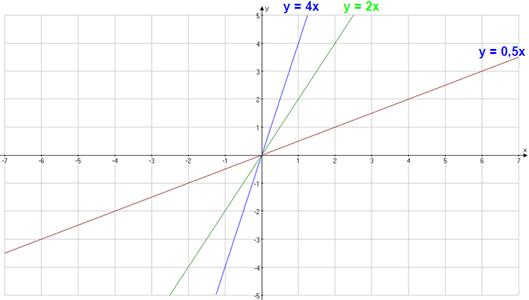
As funcións que teñen como representación gráfica unha recta que pasa pola orixe de coordenadas reciben o nome de funcións lineais. Teñen todas a forma y = mx, onde x é a variable independente, y é a variable dependente e m, o coeficiente de x, é unha constante, ten sempre o mesmo valor.

As funcións y = 4x, y = 2x, y = 0,5x ... son todas funcións lineais, xa que a súa representación gráfica é unha recta que pasa pola orixe de coordenadas. O coeficiente de x é o responsable da inclinación da recta e por iso recibe o nome de pendente. Canto maior sexa o seu valor, maior ha ser a inclinación da recta.

Dicimos que as funcións lineais son de proporcionalidade directa porque as magnitudes representadas polas súas variables independente e dependente son directamente proporcionais.

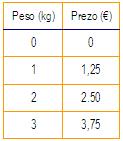
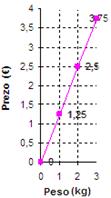
Dúas magnitudes son directamente proporcionais se se obtén unha multiplicando a outra por un número. As magnitudes de prezo e peso referidas a un produto como o azucre son directamente proporcionais. Supoñamos que 1 kg de azucre custa 1,25 euros. Se representamos por x o prezo de 1 kg e por y o custo total, a función y = 1,25x é a función asociada a esa proporcionalidade e podemos construír a táboa de valores e a representación gráfica da función.

y = 1,25x

y = 1,25·0 = 0

y = 1,25·1 = 1,25

y = 1,25·2 = 2,50

y = 1,25·3 = 3,75



Funcións afíns (y = mx+b)

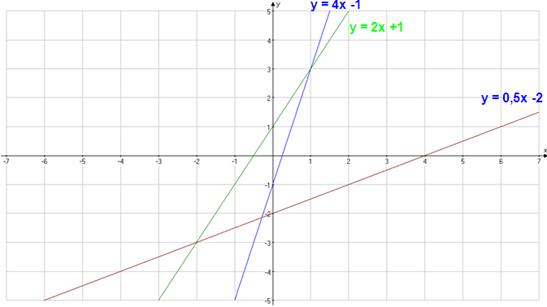
As funcións que teñen como representación gráfica unha recta que non pasa pola orixe de coordenadas reciben o nome de funcións afíns.

Teñen todas a forma y = mx + b, onde x é a variable independente, y é a variable dependente, m, o coeficiente de x, é unha constante chamada pendente e b é tamén unha constante que indica o valor da ordenada cando x = 0. É por iso que se chama ordenada na orixe.

As funcións y = 4x – 1, y = 2x + 1, y = 0,5x – 2 ... son todas afíns, xa que a súa representación gráfica é unha recta que non pasa pola orixe de coordenadas.

Funcións constantes (y =c)

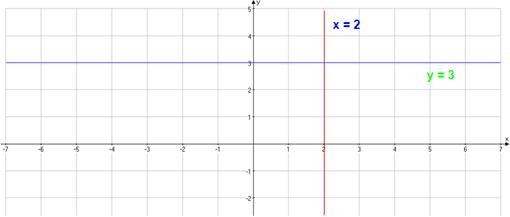
As funcións nas que calquera das variables toman sempre o mesmo valor chámanse funcións constantes. A representación destas funcións é unha recta paralela a un dos eixes.

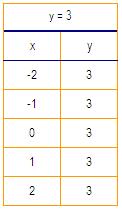
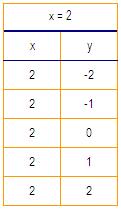
As funcións y = 3, x = 2 ... son exemplos de funcións constantes.

Se construímos a táboa de valores de cada unha delas veremos que, independentemente de cal sexa o valor da outra variable, o valor de y e de x permanece constante.

Move o deslizador m para observar cómo cambia a pendiente da función lineal e afín. Ao mover o deslizador n observarás cómo a recta cambia seu corte co eixe Y. Co movemento obterás tres tipos de funcións: Lineal, afín e constante.

Compartida por evamate - LicenciaCC-BY-SA, GeoGebra Terms of Use

Actividade resolta

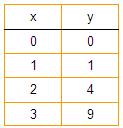
Queremos representar graficamente a función y = x² que, como xa indicamos, permite calcular a superficie dun cadrado en función do seu lado.

Construímos a táboa de valores.
Situamos os pares (abscisa e ordenada) nun sistema de coordenadas.
Unimos os puntos cunha liña.

y = x²

y = 0² = 0

y = 1² = 1

y = 2² = 4

y = 3²= 9



Actividades propostas

S14. A función que asocia a cada número enteiro o seguinte podemos escribila coa expresión alxébrica y = x + 1. Represente graficamente a función seguindo os pasos enunciados na actividade anterior.

S15. A función que asocia a cada número o seu triplo podemos escribila coa expresión alxébrica y = 3x. Represente graficamente a función seguindo os pasos coñecidos.

S16. A función que asocia a cada número enteiro a súa metade podemos escribila coa expresión alxébrica 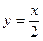. Represente graficamente a función seguindo os pasos coñecidos.