Operaciones con fracciones

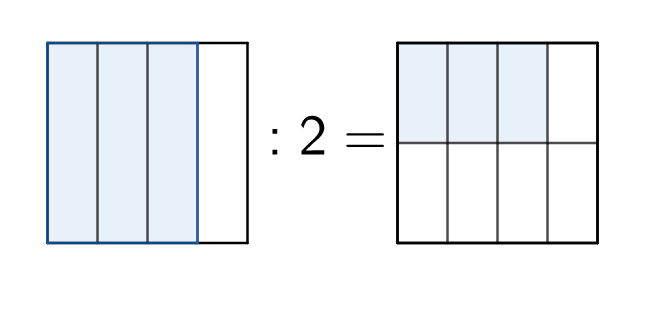
1. Suma y resta de fracciones

Suma y resta de fracciones con el mismo denominador:

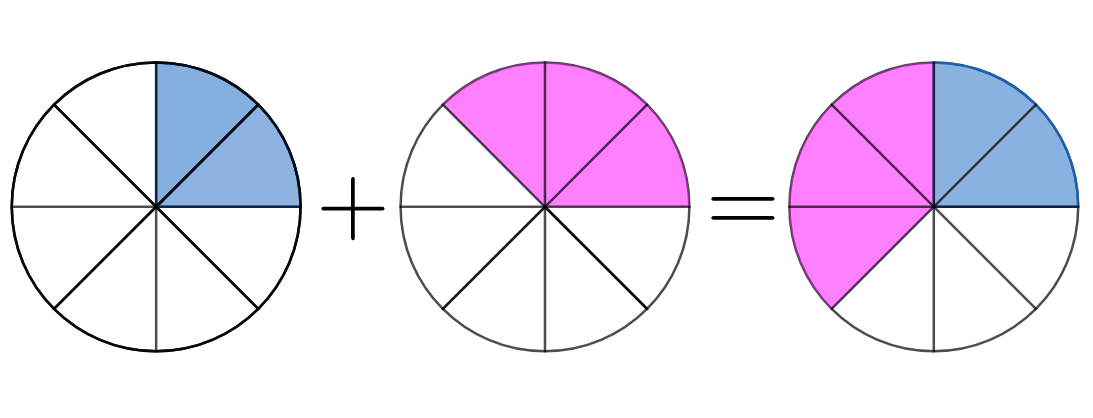
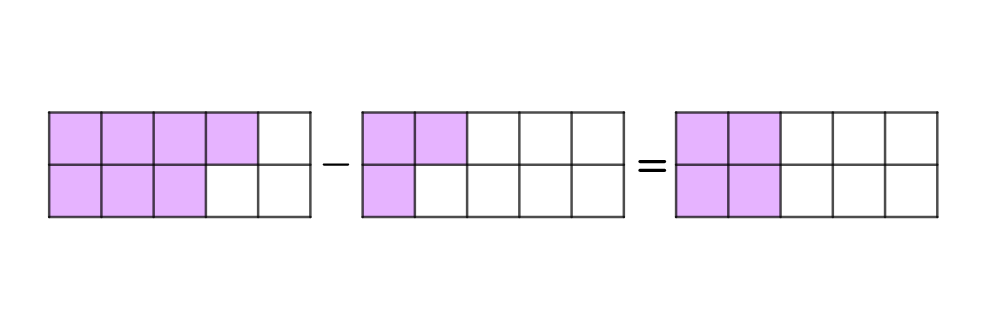
La suma o la resta de dos fracciones con el mismo denominador es otra fracción en la que en el numerador está la suma o la resta de los numeradores de esas fracciones y en el denominador el mismo denominador que tenían.

Suma

$\large \displaystyle\frac{2}{8}+\frac{3}{8}=\frac{2+3}{8}=\frac{5}{8}$

Gráficamente:

$La imagen muestra una suma gráfica de fracciones$

Resta

$\large \displaystyle\frac{7}{10}-\frac{3}{10}=\frac{7-3}{10}=\frac{4}{10}=\frac{2}{5}$

Gráficamente:

$La imagen muestra una resta gráfica de fracciones$

Audio

Suma y resta de fracciones con distinto denominador:

Paso a Paso:

1º Calculamos el mínimo común múltiplo de los denominadores

$\large \displaystyle Ejemplo\hspace{1mm} 1:\frac{1}{6}+\frac{2}{3}$ $\large \displaystyle mcm(6,3)=6$

$\large \displaystyle Ejemplo\hspace{1mm}2: \frac{2}{3}+\frac{5}{6}-\frac{3}{4}$ $\large \displaystyle mcm(3,6,4)=12$

2º Cambiamos cada fracción por otra que sea equivalente y tenga como denominador el mínimo común múltiplo calculado anteriormente.

$\large \displaystyle Ejemplo\hspace{1mm} 1: \frac{1}{6}+\frac{2}{3}=\frac{1}{6}+\frac{4}{6}=$

$\large \displaystyle Ejemplo\hspace{1mm} 2: \frac{2}{3}+\frac{5}{6}-\frac{3}{4}=\frac{8}{12}+\frac{10}{12}-\frac{9}{12}=$

3º Ahora calculamos las sumas y restas de fracciones con el mismo denominador.

$\large \displaystyle Ejemplo\hspace{1mm} 1: \frac{1}{6}+\frac{2}{3}=\frac{1}{6}+\frac{4}{6}=\frac{5}{6}$

$\large \displaystyle Ejemplo\hspace{1mm}2: \frac{2}{3}+\frac{5}{6}-\frac{3}{4}=\frac{8}{12}+\frac{10}{12}-\frac{9}{12}=\frac{8+10-9}{12}=\frac{9}{12}=\frac{3}{4}$

Audio

2. Multiplicación de fracciones

Producto de un entero por una fracción

$\large \displaystyle 4 \cdot \frac{2}{3}=\frac{4 \cdot 2}{3}=\frac{8}{3}$

Gráficamente:

Producto de dos fracciones

El producto de dos fracciones es otra fracción que tiene por numerador el producto de sus numeradores y por denominador el producto de sus denominadores

$\large\displaystyle \frac{2}{3} \cdot \frac{4}{5}=\frac{2 \cdot 4}{3\cdot 5}=\frac{8}{15}$

Gráficamente:

$La imagen muestra la multiplicación gráfica de fracciones$

Audio

3. Y ahora... visualízalo

Esta aplicación de GeoGebra permite visualizar la multiplicación de dos pequeñas fracciones que tú elijas.

El deslizador rojo representa el denominador y el numerador de la primera fracción. Los deslizadores azules representan el denominador y el numerador de la segunda fracción. Mueve los deslizadores para encontrar las fracciones a multiplicar.

https://www.geogebra.org/m/jkqxk99g (Ventana nueva)

CREAGAL,https%3A//www.geogebra.org/m/jkqxk99g,Copia%20de%20Multiplicaci%F3n%20de%20Fracciones,0,Autor%EDa

Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

4. División de fracciones.

División de una fracción entre un entero

$\large\displaystyle \frac{3}{4} :2 =\frac{3}{8}$

Observa que: $\large\displaystyle \frac{3}{4} : 2 =\frac{3}{4} \cdot \frac{1}{2}$, es decir, dividir entre un número es multiplicar por su inverso.

Gráficamente:

$La imagen muestra la división gráfica de una fracción por un entero$

División de dos fracciones

Teniendo en cuenta la observación anterior:

$\large\displaystyle \frac{2}{3} : \frac{5}{7}=\frac{2}{3} \cdot \frac{7}{5}=\frac{14}{15}$

La división de dos fracciones es otra fracción que tiene por numerador el producto del numerador de la primera por el denominador de la segunda y por denominador el producto del denominador de la primera por el numerador de la segunda.

Audio

Vamos a practicar

Imagen que muestra una joven sentada con ordenador

Ahora toca practicar un poco. Te invito a resolver esta serie de actividades.

Si ya tienes claro como se opera con fracciones no tendrás inconvenientes.

Coge papel y bolígrafo y calcula...

A: Empezamos con algo simple

Efectúa las siguientes operaciones y simplifica los resultados si es posible. Si en algún ejercicio necesitas convertir un número entero en una fracción solo tienes que ponerle un uno en el denominador como en este ejemplo: $\Large{3=\frac{3}{1}}$

$\Large{a) \hspace{1 mm}\frac{2}{7}+\frac{3}{7}-\frac{1}{7}=}$

$ \Large{b) \hspace{1 mm}\frac{3}{4}+\frac{5}{4}-\frac{2}{4}=}$

$ \Large{c) \hspace{1 mm}\frac{1}{4}-\frac{3}{4}=}$

$\Large{d)\hspace{1 mm}5- \frac{1}{2}=}$

$\Large{e) \hspace{1 mm}\frac{2}{5}-\frac{3}{10}+\frac{1}{2}=}$

$\Large{f)\hspace{1 mm}-\frac{1}{3}+\frac{1}{2}+\frac{5}{6}=}$

$\Large{g) \hspace{1 mm}2+\frac{5}{4}-\frac{3}{6}=}$

$\Large{h) \hspace{1 mm}\frac{3}{5} \cdot \frac{2}{10}=}$

$ \Large{i)\hspace{1 mm}\frac{3}{5} \div \frac{2}{10}=}$

$ \Large{j)\hspace{1 mm}\frac{2}{3} \cdot 5=}$

$\Large{k)\hspace{1 mm}2 \cdot \frac{5}{6}=}$

$\Large{l)\hspace{1 mm} \frac{3}{5} \div 2=}$

$\Large{m)\hspace{1 mm} 7 \div \frac{3}{2} =}$

$ \Large{n)\hspace{1 mm}\frac{7}{6}+\frac{4}{3}-\frac{1}{8}-\frac{3}{2}=}$

$ \Large{o)\hspace{1 mm}\frac{5}{9}+\frac{1}{5}-\frac{2}{15}+\frac{4}{3}=}$

$ \Large{p)\hspace{1 mm}\frac{2}{3} \cdot \frac{7}{10} \cdot \frac{9}{2}=}$

$\Large{q) \hspace{1 mm}\frac{1}{9}-\frac{1}{3} - \frac{1}{27}=}$

Mostrar Respuestas

$\Large{a) \hspace{1 mm}\frac{4}{7}}$

$\Large{b) \hspace{1 mm}\frac{3}{2}}$

$\Large{c)\hspace{1 mm} -\frac{1}{2}}$

$\Large{d) \hspace{1 mm}\frac{9}{2}}$

$\Large{e) \frac{3}{5}}$

$\Large{f) 1}$

$\Large{g) \hspace{1 mm}\frac{11}{4}}$

$\Large{h) \hspace{1 mm}\frac{3}{25}}$

$\Large{i) \hspace{1 mm}3}$

$\Large{j) \hspace{1 mm}\frac{10}{3}}$

$\Large{k) \frac{5}{3}}$

$\Large{l) \frac{3}{10}}$

$\Large{m) \hspace{1 mm}\frac{14}{3}}$

$\Large{n) \hspace{1 mm}\frac{7}{8}}$

$\Large{o)\hspace{1 mm} \frac{88}{45}}$

$\Large{p) \hspace{1 mm}\frac{21}{10}}$

$\Large{q) \frac{47}{27}}$

B: Ahora mezclamos

Efectúa las siguientes operaciones combinadas y simplifica los resultados si es posible.

$\large{a) \hspace{1 mm}\frac{2}{5}+\frac{1}{5}\div\frac{2}{3}=}$

$ \large{b)\hspace{1 mm}\frac{3}{5}+\frac{1}{5} \cdot \frac{3}{2}=}$

$ \large{c)\hspace{1 mm}\frac{4}{3}-\frac{2}{3} \div \frac{5}{2}=}$

$ \large{d)\hspace{1 mm}2-\frac{1}{2} \cdot \frac{3}{5}\div\frac{3}{10}=}$

$ \large{e)\hspace{1 mm}\frac{2}{5}\div\frac{1}{3} \div \frac{4}{10}=}$

$ \large{f)\hspace{1 mm}2 \cdot \frac{1}{5}-\frac{1}{3} \cdot \frac{6}{5}+ \frac{3}{5}\div \frac{5}{2}=}$

$ \large{g) \hspace{1 mm}\frac{7}{2}-\frac{1}{5} \div \frac{2}{3}+ 2 \div \frac{5}{4}=}$

$ \large{h)\hspace{1 mm} \frac{3}{2}-\frac{1}{4} +\frac{3}{8}- \frac{5}{16}=}$

$ \large{i)\hspace{1 mm} \frac{2}{7}\cdot \frac{3}{2} -\frac{2}{7}\div \frac{7}{5}=}$

$ \large{j)\hspace{1 mm} \frac{4}{3}+\frac{1}{6} \div\frac{2}{3}- \frac{8}{3}\div \frac{3}{2}=}$

$ \large{k)\hspace{1 mm} \frac{2}{5} \cdot \frac{1}{3} +\frac{1}{3} \cdot \frac{1}{3}- \frac{3}{5}=}$

Y ahora con paréntesis:

$ \large{l)\hspace{1 mm}\left(\frac{2}{5}+\frac{1}{5}\right) \div \frac{7}{10}=}$

$ \large{m)\hspace{1 mm}\left(2-\frac{1}{5}\right) \div \left(3+\frac{1}{2}\right)=}$

$ \large{n)\hspace{1 mm}\left[\left(1+\frac{2}{3}\right)\cdot \frac{5}{2}-\frac{1}{2}\right]-3=}$

$ \large{o)\hspace{1 mm}3-\frac{1}{4} \cdot \left(\frac{5}{2}+\frac{3}{10}\right)=}$

Mostrar Respuestas

$\Large{a)\hspace{1 mm} \frac{7}{10}}$

$\Large{b) \hspace{1 mm}\frac{9}{10}}$

$\Large{c) \hspace{1 mm}\frac{16}{15}}$

$\Large{d)\hspace{1 mm} 1}$

$\Large{e)\hspace{1 mm} 3}$

$\Large{f) \hspace{1 mm}\frac{6}{25}}$

$\Large{g) \hspace{1 mm}\frac{24}{5}}$

$\Large{h) \hspace{1 mm}\frac{21}{16}}$

$\Large{i) \hspace{1 mm}\frac{11}{49}}$

$\Large{j)\hspace{1 mm} -\frac{7}{36}}$

$\Large{k) \hspace{1 mm}-\frac{16}{45}}$

Y con los paréntesis:

$\Large{l) \hspace{1 mm}\frac{6}{7}}$

$\Large{m)\hspace{1 mm} \frac{18}{35}}$

$\Large{n) \hspace{1 mm}\frac{2}{3}}$

$\Large{o) \hspace{1 mm}\frac{23}{10}}$

D: Otro de depósitos

El indicador del depósito de la inspectora Cruxeiras acababa de marcar que ha llegado a la reserva (zona roja), por lo que fue a la gasolinera, le echó 42 litros de gasolina y llenó el depósito.

La imagen muestra el indicador de gasolina de un coche

E: Una de telas

Enrique acude a una tienda de retales a comprar tela para coser unas cortinas para el pazo de Taboada. Le pide al dependiente que le corte la mitad de un rollo de tela de terciopelo. Cuando está saliendo del comercio, piensa en hacer unos cojines a juego y le pide al dependiente que le corte un cuarto del género que quedaba en el rollo. ¿Qué fracción del rollo ha comprado en total Enrique? ¿Qué fracción del rollo queda en la tienda?

F: Y acabamos con una de sidra

La familia Trastámara hace sidra con las manzanas que recolecta en la finca que tienen al lado de su casa. Al prensar manzanas, se obtienen $\Large\frac{4}{11}$ de su peso en zumo y el resto son residuos triturados. ¿Qué fracción del peso representan los residuos del prensado?

Reflexiona...

¿Has visto los pasos que has dado para resolver los problemas de fracciones?

Durante esta actividad, has puesto en práctica todo lo que sabes. A veces, el aprendizaje requiere esfuerzo constante. Cuando nos dedicamos con empeño, nuestros profesores y familiares valoran nuestro trabajo. Sin embargo, lo más importante es que nos sentimos felices por lo que hemos logrado. Te animo a seguir trabajando para seguir aprendiendo y mejorando.

Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0

Suma

Resta

1º Calculamos el mínimo común múltiplo de los denominadores

2º Cambiamos cada fracción por otra que sea equivalente y tenga como denominador el mínimo común múltiplo calculado anteriormente.

3º Ahora calculamos las sumas y restas de fracciones con el mismo denominador.

Pregunta

Respuestas

Retroalimentación

Solución

Pregunta

Respuestas

Retroalimentación

Solución

Pregunta

Respuestas

Retroalimentación

Solución

Pregunta

Respuestas

Retroalimentación

Solución