1. ¿Cómo opero con decimales?
Presta atención, porque cada operación tiene sus propiedades:
Suma y resta
Para sumar o restar números decimales tenemos que sumar o restar unidades con unidades, décimas con décimas... Por tanto, si indicamos esta operación en columna, debemos colocar las unidades encima de las unidades, las décimas encima de las décimas, las centésimas encima de las centésimas..., es decir, debemos situar las comas encima de las comas.
\(\large \displaystyle \text{Colocación incorrecta}\)
\(\large \displaystyle \hspace{5 mm}135,5\)
\(\large \displaystyle \hspace{7 mm} 1,52\)
\(\large \displaystyle +\hspace{1 mm} 23,11\)
\(\rule{25mm}{0.4mm}\)
\(\large \displaystyle \text{Colocación correcta}\)
\(\large \displaystyle \hspace{2,5 mm}135,5\)
\(\large \displaystyle \hspace{8,25 mm} 1,52\)
\(\large \displaystyle +\hspace{1 mm} 23,11\)
\(\rule{25mm}{0.4mm}\)
\(\large \displaystyle \hspace{2,5 mm} 160,13\)
Multiplicación
La multiplicación de números decimales se realiza de igual manera que la multiplicación de números enteros. Solamente debemos tener en cuenta que, en el producto final, colocaremos la coma dejando tantas cifras decimales como reúnan todos los factores.
\(\large \displaystyle \hspace{15 mm}5,5\hspace{2 mm}2\)
\(\large \displaystyle \hspace{8 mm} \times \hspace{6 mm}3,5\)
\(\rule{35mm}{0.4mm}\)
\(\large \displaystyle \hspace{12 mm} 2 \hspace{2 mm} 7 \hspace{2 mm} 6 \hspace{2 mm} 0\)
\(\large \displaystyle \hspace{1 mm} 1 \hspace{2 mm} 6 \hspace{2 mm} 5 \hspace{2 mm} 6\)
\(\rule{35mm}{0.4mm}\)
\(\large \displaystyle \hspace{3 mm} 1 \hspace{2 mm} 9, 3 \hspace{2 mm} 2 \hspace{2mm} 0\)
Ahora combinando
Las reglas de jerarquía y el orden de operaciones se mantienen para los números decimales. Recuerda el orden:
Paréntesis.
Potencias.
Productos y divisiones.
Sumas y restas.
Audio
SUMAS Y RESTAS
MULTIPLICACIÓN
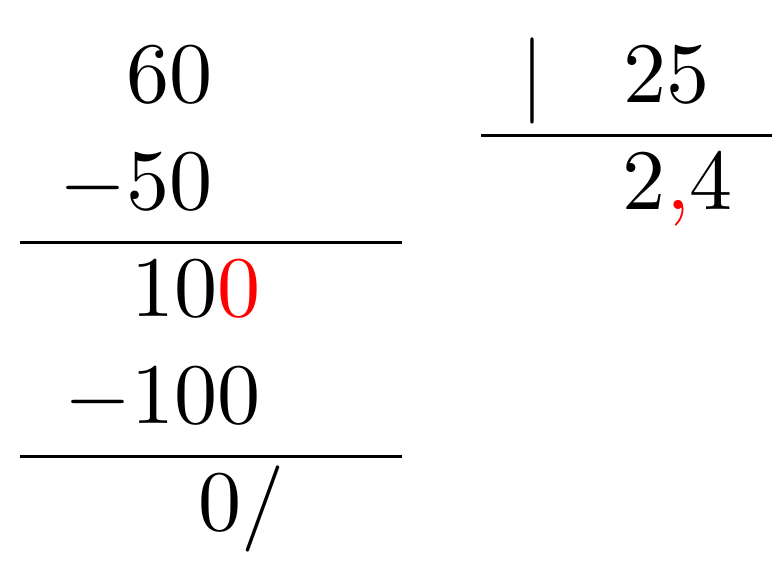
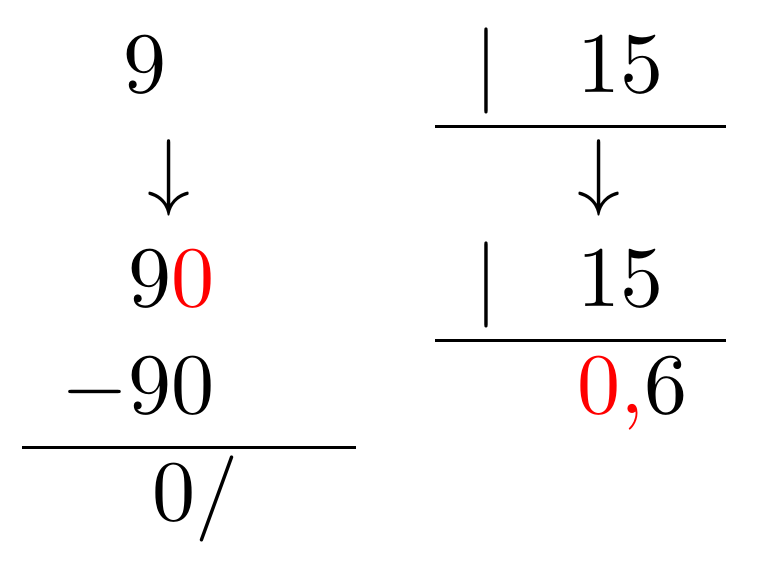
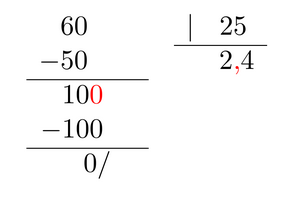
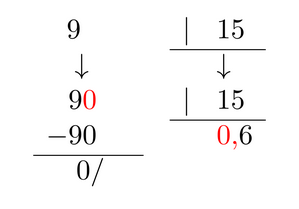
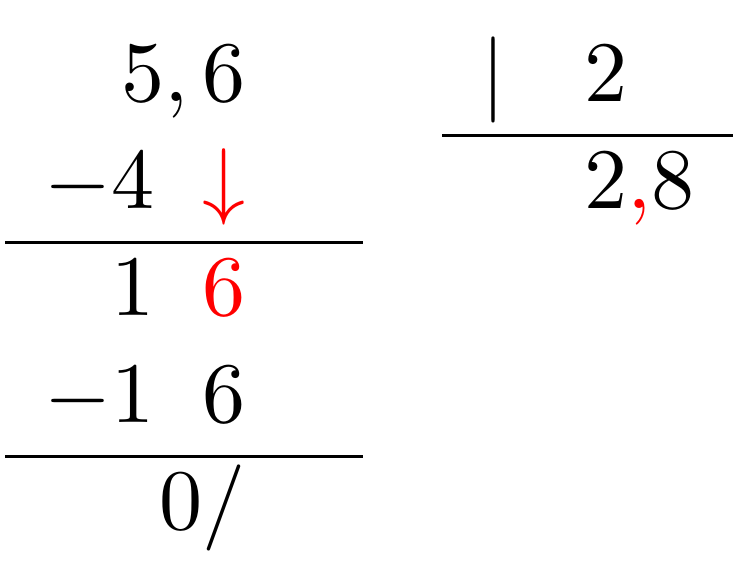
Cuando multiplicamos un número decimal por 10, por 100, por 1000... lo que hacemos es desplazar la coma hacia la derecha tantos lugares como ceros contiene nuestro entero. Esto es, un lugar en el caso del 10, dos lugares en el caso del 100, tres lugares en el caso del 1000, y así sucesivamente. Si es necesario, se añaden ceros a la derecha.
Del mismo modo, cuando multiplicamos por 0,1 ; por 0,01; por 0,001;... lo que hacemos es desplazar la coma hacia la izquierda tantos lugares como decimales tengamos. Así pues, si multiplicamos por 0,1 desplazamos la coma hacia la izquierda un lugar, si multiplicamos por 0,01 desplazamos la coma dos lugares, y así sucesivamente. Si es necesario, se añaden ceros a la izquierda.
