Saltar la navegación

3.4. Los perfiles y sus valores

La ruta de las algas

A la hora de plantear tu ruta por patrimonio oculto debes decidir si esta será lineal, circular o de ida y vuelta.

Ruta lineal

Comienza en un punto y termina en un punto final distinto.

Ruta circular

Comienzan y terminan en el mismo punto siguiendo un sólo camino.

Ruta de ida y vuelta

Comienzan y terminan en el mismo punto, pero a diferencia de la ruta circular llegan hasta un lugar final y vuelven por el mismo camino.

Captura de imagen de Google Earth con la ruta de las algas marcada en rojo.

Imagina que acabas de realizar la Ruta lineal de las Algas, en la costa de Loiba (A Coruña):

Punto de partida:

Acceso a la "Ribeira do Carro": 43°44'10" N 7°45'53" W.

Punto de destino:

Pasarela a la playa de Esteiro: 43°44'43" N 7°43'38" W

A lo largo de la Ruta de las Algas encontrarás playas pequeñas a los pies de grandes acantilados. Esta costa tan espectacular pertenece al Geoparque del Cabo Ortegal, un territorio de interés geológico reconocido a nivel mundial por la UNESCO.

La Ruta de las Algas utiliza caminos que bajan en zig-zag a playas que quedan ocultas en la pleamar, y que antiguamente usaban las mujeres que recogía las algas de la costa para venderlas o usarlas para diversos fines.

Los números explican el cansancio

Esta ruta es realmente agotadora porque está llena de subidas y bajadas, pero ¿podrás conocer la cantidad de metros que has subido y bajado?

Altitudes

La altitud inicial es de 116 m y la final de 12 m. 

Entonces, ¿te encuentras más arriba o más abajo? ¿Has subido o bajado solo esa distancia? 

¿Qué está pasando?

Perfil de ruta

En el folleto de la ruta aparecía esta imagen del perfil de ruta: 

Gráfico con perfil simplificado. Distancia recorrida en el eje horizontal y altitud correspondiente, en metros, en el vertical.

Entonces, ¿Cuál es la distancia que has bajado? ¿Cuál es la distancia que has subido? ¿Cuál es la diferencia entre la distancia de subida y la distancia de bajada?

Pista

Para calcular la distancia subida y distancia bajada debes observar los kilómetros recorridos, es decir, tener en cuenta los valores del eje X del perfil de ruta y analizar la altitud para saber si te encuentras en un tramo de subida o de bajada. 

Recuerda que el perfil de elevación de ruta o perfil de ruta te permite visualizar la vista lateral para conocer datos de elevación a lo largo de una línea.      Tabla de 17 filas, una fila por tramo, y 4 columnas (distancia, altitud, tramo bajada, tramo subida)

Solución

Tabla de datos I

Estos son los datos que puedes extraer del perfil de ruta: 

Tabla Loiba Datos

Tramos de subida y tramos de bajada

Ahora teniendo en cuenta los metros bajados y subidos los escribes en la columna correspondiente. 

Tabla de 17 filas, una fila por tramo, y 4 columnas (distancia, altitud, tramo bajada, tramo subida)

Suma y restas agrupando

Si agrupas los cálculos por los metros subidos y los metros bajados y después los restas obtienes la siguiente información: 

Distancia en metros de subida: 

300 + 100 + 200 + 500 + 300 + 300 + 500 = 2200 m

Distancia en metros de bajada: 

300 + 300 + 900 + 200 + 200 + 500 + 400 + 200 + 800 = 3800 m

Ahora puedes ver la diferencia entre los tramos de bajada y de subida:

2200 - 3800 = -1600 m

¡Has recorrido 1600 metros más de bajada que de subida!

Suma y resta de izquierda a derecha

De esta forma, irás haciendo sumas y restas según sea un trabajo de bajada o de subida:

300 - 300 + 300 + 900 - 100 + 200 - 200 + 200 - 500 + 500 - 300 + 400 - 300 + 200 + 800 - 500 = 1600 m

¡Has recorrido 1600 metros más de bajada que de subida!

Como puedes observar obtienes el mismo resultado mediante dos métodos diferentes y esto en matemáticas ocurre en múltiples ocasiones. 

Practica cuestas y cuentas

En esta actividad puedes comprobar cuántos metros más de cuestas arriba o abajo hay en una ruta a partir de su perfil. 

¡Y de dos formas distintas!

https://www.geogebra.org/m/rzbubpn6 (Ventana nueva)

Proxecto%20cREAgal,https%3A//www.geogebra.org/m/rzbubpn6,GG_MAT1ESO_REA02%20Copia%20de%20Tramos%20de%20subida%20y%20bajada%20en%20perfil%20de%20ruta,1,Autor%EDa
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

Variaciones y desniveles

Para poder estudiar el desnivel acumulado y los tramos de subida y bajada habrás observado que Navia y Bandua han recurrido al perfil de elevación de la ruta en las dos que han realizado.

¿Por qué es importante el perfil de elevación? A la hora de planificar una ruta necesitas analizar su perfil para saber si te va a suponer mucho o poco esfuerzo recorrerla. Si haces una ruta lineal que empieza a una altitud elevada y superior a la de los puntos que vas a visitar, habrá muchos tramos de bajada, ¡casi no necesitarás esforzarte! En cambio, si tu ruta tiene muchos tramos de subida tendrás que estar pendiente de reservar fuerzas para llegar hasta el final.

El perfil de ruta es una gráfica que en la vertical muestra la altitud a la que estás en cada punto del recorrido. En la horizontal muestra la distancia que has recorrido. Esta información te permite estudiar los tramos de subida y bajada como hicieron Navia y Bandua en las viñetas del principio.

También puedes calcular otros parámetros. Te los explicamos a continuación:

Variación de la altitud

La variación de la altitud se mide calculando la diferencia entre la altitud la final y la inicial.

variación altitud = altitud final - altitud inicial

  • Si la variación de altitud total de una ruta es positiva es porque la ruta acaba a una altitud superior.
  • Si la variación de altitud total de una ruta es negativa es porque la ruta acaba a una altitud inferior.

La variación máxima de altitud es la diferencia entre el punto más alto y más bajo de la ruta. 

variación máxima = mayor altitud - menor altitud

Ejemplo:

Aroa y Noa parten de una altitud de 15 metros, suben a una altitud de 100 metros y descienden a 50 metros de altitud donde paran a descansar. Luego suben a una altitud de 250 metros y descienden a una altitud de 225 metros.

  • ¿Qué variaciones de altitud hay a lo largo de la ruta?

variación1 = 100 - 15 = 85 metros
variación2 = 50 - 100 = - 50 metros
variación3 = 250 - 50 = 200 metros 
variación4 = 225 - 250 = - 25 metros

  • ¿Cuál es la variación de altitud total de la ruta?

variación total = 225 - 15 = 210 metros

  • ¿Cuál es la variación máxima de la ruta?

variación máxima = 250 - 15 = 235 metros

Desniveles: neto, positivo y negativo

  • El desnivel positivo se calcula sumando las variaciones de altitud positivas de una ruta, es decir, solo se tienen en cuenta las subidas.
    En las rutas ciclistas encontrarás referencias al desnivel positivo ya que nos permite calcular y comparar la dificultad de las rutas.
  • El desnivel negativo se calcula sumando las variaciones de altitud negativas de una ruta, es decir, solo se tienen en cuenta las bajadas.
    En las pistas de ski lo interesante es calcular el desnivel negativo ya que nos permite compararlas.
  • Si sumas el desnivel positivo y el negativo, también obtienes el desnivel neto que coincide con la variación total de la ruta, pero mediante una fórmula distinta:

desnivel neto = desnivel positivo + desnivel negativo

Siguiendo con el ejemplo anterior:

  • ¿Cuál es el desnivel positivo?

variación1 + variación3 = 85 + 200 = 285 metros de desnivel positivo

  • ¿Cuál es el desnivel negativo?

variación2 + variación4 = (- 50) + (- 25) = - 50 - 25 = - 75 metros de desnivel negativo

  • Comprobación de la fórmula que relaciona los tres conceptos con la variación total:

desnivel neto = 285 + (- 75) = 285 - 75 = 210 metros que coincide con la variación total

Desnivel acumulado

En matemáticas el desnivel acumulado se calcula sumando todas las subidas y todas las bajadas en valor absoluto.

El desnivel acumulado del ejemplo anterior es

85 + |- 50| + 200 + |- 25| = 85 + 50 + 200 + 25 = 360 metros de desnivel acumulado

También puedes calcularlo mediante la fórmula

desnivel acumulado = desnivel positivo + |desnivel negativo|

Puedes comprobarlo con el ejemplo anterior:

desnivel positivo + |desnivel negativo| = 285 + |- 75| = 285 + 75 = 360 metros de desnivel acumulado

La ruta circular

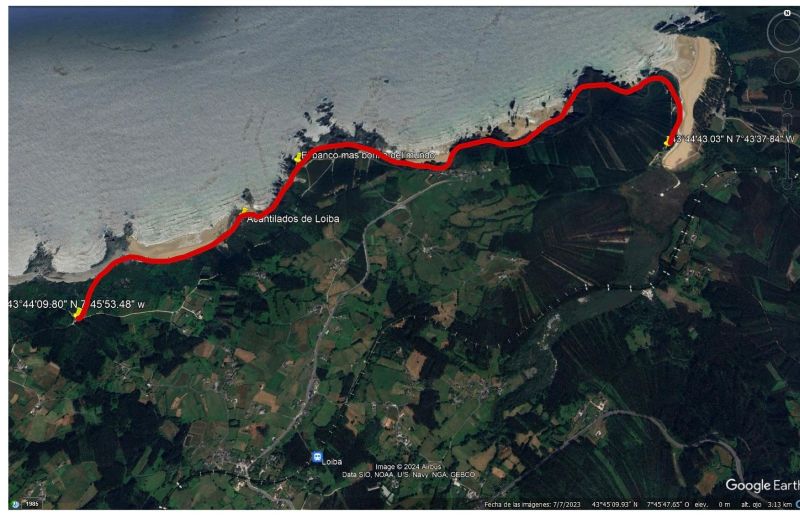
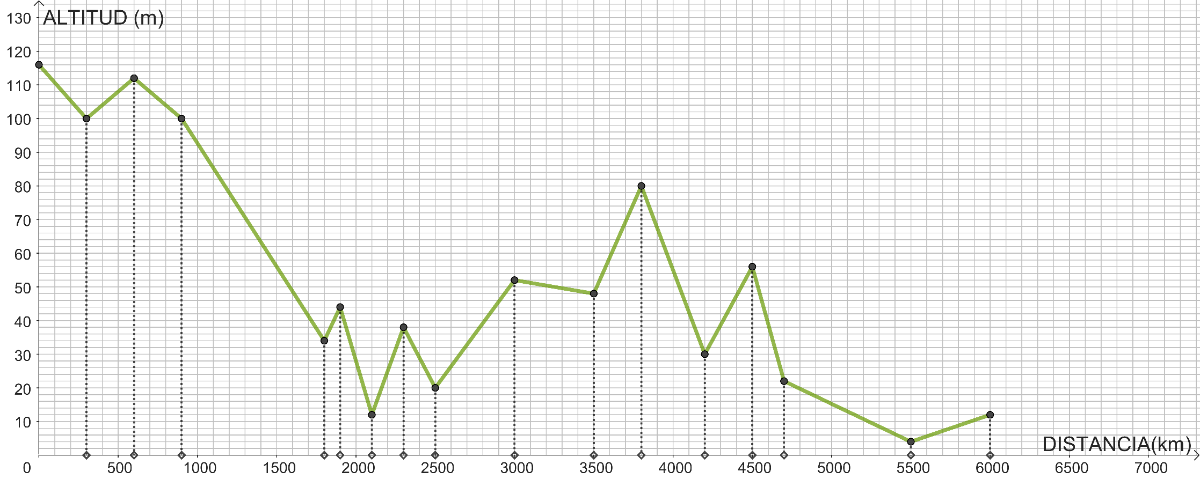
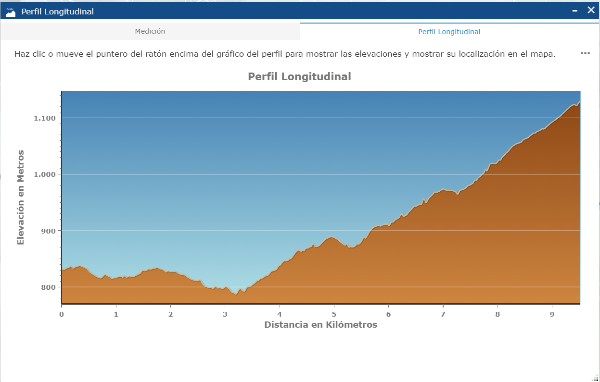
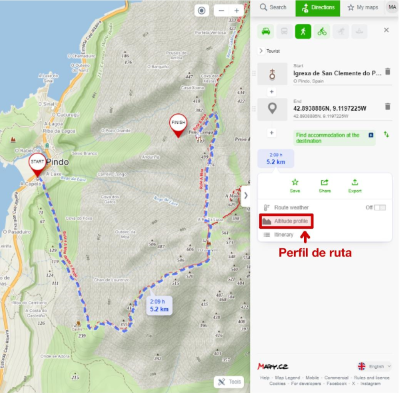
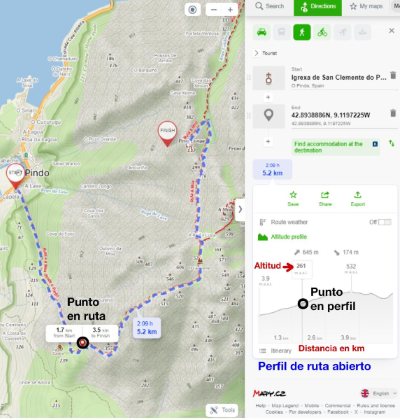
El siguiente perfil pertenece a una prácticamente ruta circular. La ruta comienza y acaba a una altitud de 544 metros como puedes ver en la primera imagen.

 

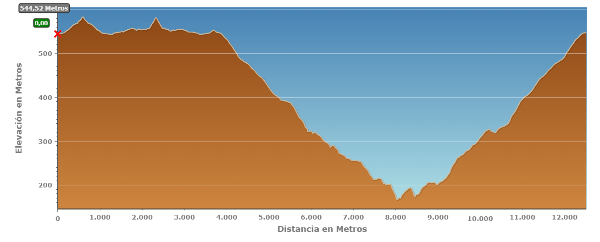
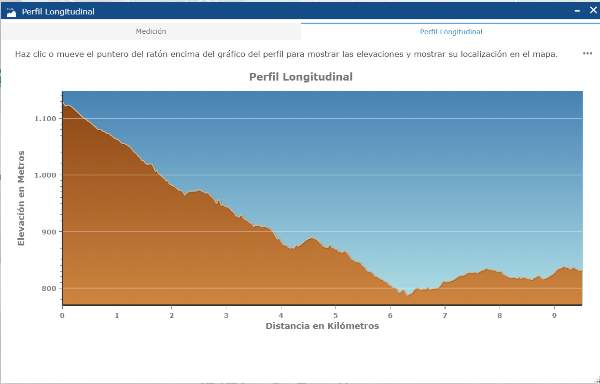
En la ruta anterior hay muchas subidas y bajadas. Cuando esto ocurra, puedes simplificar los cálculos centrándote en las subidas y bajadas más importantes.

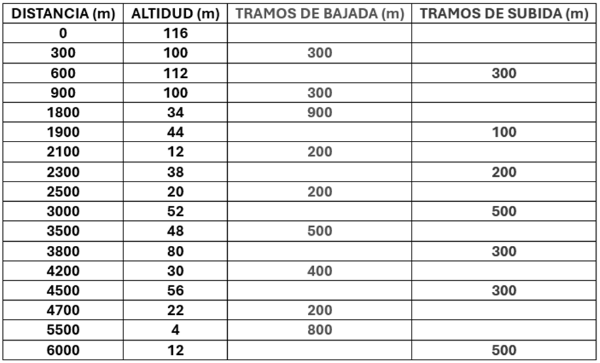
Fíjate en cómo lo hacemos en la siguiente imagen: se marcan cuatro subidas, en verde y tres bajadas, en morado. Se obtienen 7 tramos.

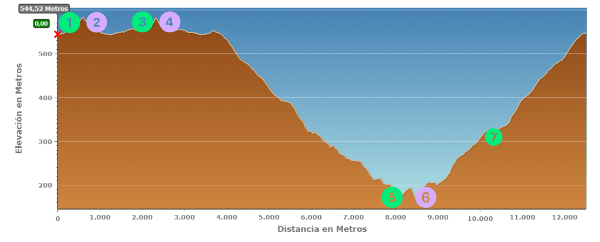
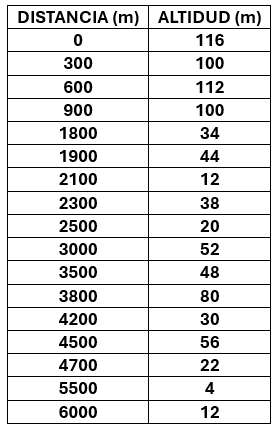
El programa signA te permite conocer las altitudes del principio y del final de cada tramo:

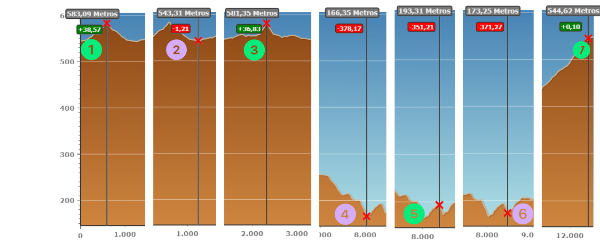
Las variaciones de altitud son las siguientes:

variación1 = 583 - 544 = 39 metros

variación2 = 543 - 583 = - 40 metros

variación3 = 581 - 543 = 38 metros

variacion4 = 166 - 581 = - 415 metros

variación5 = 193 - 166 = 27 metros

variación6 = 173 - 193 = -20 metros

variación7 = 544 - 173= 371 metros

Variación de altitud total de la ruta. Al ser una ruta circular que empieza y acaba a la misma altitud, la variación de altitud de la ruta es de 0 metros.

variación total = 544 - 544 = 0 metros

Variación máxima de la altitud. El punto más alto de la ruta se encuentra a 583 metros y el más bajo a 166 metros.

variación máxima = 583 - 166 = 417 metros

Desnivel positivo. El desnivel positivo es la suma de las subidas 1, 3, 5 y 7.

variación1 + variación3 + variación5 + variación7 = 39 + 38 + 27 + 371 = 475 metros de desnivel positivo

Desnivel negativo. El desnivel negativo es la suma de las bajadas 2, 4 y 6.

variación2 + variación4 + variación6 = (- 40) + (- 415) + (- 20) = - 40 - 415 - 20 = - 475 metros de desnivel negativo

En este caso coinciden ambos desniveles porque es una ruta circular con variación de altitud de 0 metros y por lo tanto:

desnivel positivo = | desnivel negativo | 

desnivel negativo = Op(desnivel positivo)

Desnivel acumulado. Puedes calcular el desnivel acumulado de las rutas circulares de dos formas:

La primera forma:

desnivel acumulado = | variación1 | + | variación2 | + | variación3 | + | variación4 | + | variación5 | + | variación6 | + | variación7 | =

= 39 + | - 40 | + 38 + | - 415 | + 27 + | - 20 | + 371 = 39 + 40 + 38 + 415 + 27 + 20 + 371 = 950 metros

La segunda forma que consiste en acumular positivos y negativos previamente:

desnivel acumulado = desnivel positivo + | desnivel negativo | = 475 + | - 475 | = 475+ 475 = 950 metros


Al ser una ruta circular y observando esta última operación, ¿se te ocurre una tercera forma de calcular el desnivel acumulado?

Practica jugando con los desniveles

En esta actividad puedes calcular los distintos desniveles de una ruta a partir de su perfil y comprobar los resultados.

Puedes generar nuevos perfiles en el botón o arrastrando los puntos. 

https://www.geogebra.org/m/juusjcwp (Ventana nueva)

Proxecto%20cREAgal,https%3A//www.geogebra.org/m/juusjcwp,GG_MAT1ESO_REA02%20Copia%20de%20Desniveles%20de%20altitud%20en%20perfil%20de%20ruta%20,1,Autor%EDa
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n

Perfil frente al espejo

Es importante decidir en qué sentido vas a realizar tu ruta ya que, dependiendo de las subidas y las bajadas, esta decisión afectará a la dificultad de tu ruta.

Dada las capturas de pantalla de la siguiente ruta, contesta a las preguntas formuladas:

    

Simplifica el perfil

Los perfiles reales tienen muchas pequeñas subidas y bajadas y por eso en el ejemplo anterior te propusimos una simplificación.

Selecciona las subidas y bajadas más importantes del perfil de ruta de la izquierda.

Obtén en total un mínimo de 7 tramos.

Intuye y estima

Ya sabemos que te faltan datos exactos, pero ahora lo importante es tu capacidad para estimar valores.

Tu intuición matemática es tu aliada y cuanto más la trabajes, más preciso podrás ser.

Halla de forma aproximada en el perfil de la ruta de la izquierda:

  1. La altitud inicial y final. La variación total de altitud.
  2. Las variaciones de altitud de cada tramo seleccionado.
  3. La variación máxima de la ruta.
  4. El desnivel positivo.
  5. El desnivel negativo.
  6. El desnivel acumulado.

Relaciona y deduce

Usa conceptos matemáticos para analizar qué relación hay entre la ruta de la izquierda y la de la derecha.
Usa los datos que estimaste en el apartado anterior y justifica los siguientes valores sobre el perfil de la derecha:

  1. La variación total de altitud.
  2. La variación máxima de la ruta.
  3. El desnivel positivo.
  4. El desnivel negativo.
  5. El desnivel acumulado.

Dureza de las rutas

¿Cuál de las dos rutas tendrá mayor dificultad? ¿La de la izquierda o la de la derecha?

Justifica tu respuesta usando los datos que hallaste en los apartados anteriores.

Los imprescindibles: tu ruta tiene perfil

Ahora que ya habéis visto lo que es el perfil de una ruta, es el momento de hacer el de vuestra ruta por vuestro patrimonio oculto. 

Pero lo haremos en una plataforma diferente. Trata de seguir los pasos que se indican y así conseguirás crear automáticamente tu perfil de ruta. 

1º Recopila

Busca la información sobre las coordenadas y altitud de los puntos de interés recogida en el apartado 2.2. ¿Dónde aparecen? Con la ficha de trabajo de "Los imprescindibles: coordenadas para orientarnos". 

Acceded a la página de mapy

https://en.mapy.cz/turisticka?x=-8.1147643&y=42.6727338&z=9

2º Introduce

  1. Abre la pestaña “Directions” para crear tu ruta. Ahí aparecerán dos cajas de entrada “Start” (Inicio) y “End” (Final) y si la realizarás a pie o en bicicleta. 
  2. Introduciendo las coordenadas del inicio y del final de tu ruta se generarán diferentes rutas alternativas. Ten en cuenta que en Mapy el oeste no se escribe con “O”, sino con la “W” de la palabra inglesa West.
  3. Entre el punto inicial y final puedes introducir las paradas intermedias, pulsando los
    símbolos “+” que aparece entre las cajas de entrada e introduciendo las coordenadas. 

 Introducir coordenadas. 

Introducir paradas intermedias.

3º Traza tu ruta

Para generar el perfil de la ruta, debes pulsar sobre “Altitude Profile”, en la columna derecha de la imagen, bajo las cajas de entrada del punto anterior.

Existe una correspondencia entre cada punto de la ruta con un punto del perfil. Puedes mover los puntos y ver la altitud a la que se encuentran y la distancia a la que están del inicio y del final de la ruta.

Guarda la imagen del perfil de ruta, ya que luego la incluirás en tu folleto. 

Perfil de ruta 

Correspondencia puntos.

4º Altitudes

Busca en el perfil de tu ruta las altitudes de los puntos clave de tu ruta. 

5º Calcula

Ahora con las altitudes de los puntos clave debes calcular: 

a. La variación total de la altitud.
b. La variación máxima de la ruta.
c. El desnivel positivo.
d. El desnivel negativo.
e. El desnivel acumulado.

Definiciones

Sumas y restas de izquierda a derecha o agrupando

Operando de izquierda a derecha

         1 – 2 + 3 – 5 – 2 + 4 = – 1 + 3 – 5 – 2 + 4 = 2 – 5 – 2 + 4 = – 3 – 2 = – 1

Agrupando en dos paréntesis

Agrupando todos los sumandos positivos en un paréntesis y todos los negativos en otro. 

1 – 2 + 3 – 5 – 2 + 4 = (1 + 3 + 4) – (2 + 5 + 2) 

Luego calculas el resultado de los dos paréntesis ( son todo sumas).

(1 + 3 + 4) – (2 + 5 + 2) = 8 – 9      

Terminas haciendo una única resta.

8 – 9 = – 1

Todo seguido:

1 – 2 + 3 – 5 – 2 + 4 = (1 + 3 + 4) – (2 + 5 + 2) = 8 – 9 = – 1   

Sumas y restas en las que aparecen paréntesis

Cuando te encuentras una operación en la que aparecen sumas y restas dentro de un paréntesis puedes hacerla de dos formas:

Ejemplo:

(4 – 2 + 3 ) – (1 + 2 – 5) + (2 – 3) 

Por prioridad

      (4 – 2 + 3 ) – (1 + 2 – 5) + (2 – 3) = 5 – (-2) + (–1) = 5 + 2 – 1 = 7 – 1 = 6

Eliminado paréntesis

Para quitar un paréntesis precedido de un signo +, deberás mantener el signo de todos los números que estén dentro del paréntesis.

Para quitar un paréntesis precedido de un signo –, deberás cambiar el signo de todos los números que estén dentro del paréntesis.

(4 – 2 + 3 ) – (1 + 2 – 5) + (2 – 3) =

= 4 – 2 + 3 – 1 – 2 + 5 + 2 – 3 =

Y ahora, agrupas o vas de izquierda a derecha:

= 14 – 8 = 6

Creado con eXeLearning (Ventana nueva)