6.1. Solucións das actividades propostas
S1.
A través da páxina www.ine.es, poderá comprobar que o INE, é o Instituto nacional de Estatística e atopará a que se dedica.
S2.
- Peso ao nacer dos cativos que naceron en Barcelona en 2009: Variable estatística continua.
- Profesións que queren estuda ros estudantes dun centro escolar: Variable estatística cualitativa
- Número de cartóns amarelas amosadas nos partidas de fútbol da liga do ano pasado: Variable estatística discreta.
S3.
Para realizar unha mostraxe podémolo facer por sorteo, e diremos que é unha mostraxe aleatoria simple. Se a poboación se divide en estratos que clasifican os seus elementos (idade, tipo de traballo, sexo) e coñecemos a súa proporción, convén respectar a proporción ao elixir a mostra, trátase dunha mostraxe estratificada.
S4.
|
Variable |
Frecuencia absoluta |
|
0 |
9 |
|
1 |
10 |
|
2 |
12 |
|
3 |
9 |
|
4 |
8 |
|
5 |
2 |
|
Total |
50 |
S5.
|
Variable |
Frecuencia absoluta |
|
MB |
6 |
|
B |
9 |
|
R |
27 |
|
M |
5 |
|
MM |
3 |
|
Total |
50 |
- Se sumamos o número de persoas que responden M ou MM, resultan ser 8.
- Se sumamos o número de persoas que responden B ou MB resultan ser 15, que son o 30 % do total.
S6.
|
Variable |
Frecuencia absoluta |
|
0 |
0 |
|
1 |
2 |
|
2 |
6 |
|
3 |
9 |
|
4 |
18 |
|
5 |
22 |
|
6 |
24 |
|
7 |
12 |
|
8 |
7 |
|
Total |
100 |
- Os alumnos que obteñen 5 puntos son 22 e representan o 22 % do total
- Os alumnos que reciben 6 ou máis puntos son 24+12+7 = 43, e son o 43%.
S7.
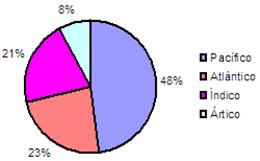
S8.
- Notas.
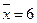 ,
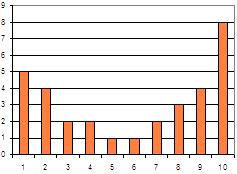
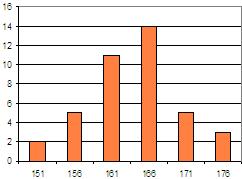
, 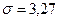 Sendo a desviación típica 3,27, parece claro que os datos desta táboa están bastante dispersos con respecto á media, o que se observa no diagrama de barras:
Sendo a desviación típica 3,27, parece claro que os datos desta táboa están bastante dispersos con respecto á media, o que se observa no diagrama de barras:
- Estaturas:
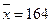 ,
, 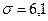 Aquí, pola contra, temos pouca desviación con respecto á media, os datos están agrupados en torno a ela.
Aquí, pola contra, temos pouca desviación con respecto á media, os datos están agrupados en torno a ela.
S9.
|
|
|
|
|
|
S10.
- 1) E = {1,2,3,4,5} Sucesos elementais A = {1}, B = {2}, C = {3}, D= {4}, F ={5} Suceso composto G = { 1, 2} Suceso seguro = {sacar menos de 5} Suceso imposible = { sacar máis de 6}.
- 2) E = {verde, amarelo, azul, laranxa, carne} Sucesos elementais A = {verde} Suceso composto {verde, carne} Suceso seguro ={sacar verde ou carne ou azul ou laranxa ou amarelo} Suceso imposible ={vermello}
S11.
- Espazo mostral
E = { (1,1,), (1,2),(1,3),(1,4),(1,5),(1,6),(2,1),..................................………(6,1), (6,2),(6,3),(6,4),(6,5),(6,6)}
- Suceso A = {obter unha parella de números iguais} = {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6)}
- Suceso B = {Obter 8 puntos na tirada} = { (2,6),(3,5),(4,4),(5,3), (6,2) }
S12.
- No caso da chincheta non se trata de sucesos equiprobables, como vimos no exemplo. No caso das bólas, tampouco, xa que o número de bolas brancas e negras é distinto.
S13.
- p(sexa comedia) =
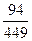
- p(non sexa drama) =
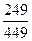
S14.
- p(sacar 3) =
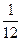
- p(sacar múltiplo de 3) =
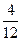
- p(non sacar múltiplo de 3) =
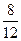
- p( sacar negativo) = 0
- p(sacar < 20) = 1
S15.
- p(suma sexa 2) =
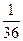
- p(suma sexa 1) = 0. Suceso imposible
- p (suma sexa <6) =
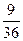
- O seu suceso contrario será sacar maior ou igual a 6 e a súa probabilidade será=
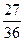
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0