2.2.3 Lei de Laplace para o cálculo da probabilidade
Cando estamos ante un experimento aleatorio en que todos os sucesos elementais teñen a mesma probabilidade de saír, dicimos que son equiprobables. Sería o caso do lanzamento dun dado, todos os los números teñen a mesma probabilidade de saír
Se calculamos o espazo mostral, estamos ante un espazo de sucesos equiprobables. Nesta situación a regra de Laplace di o seguinte:
-
-
Regra de Laplace
A probabilidade de que se verifique un suceso A é:
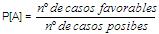
-
Exemplo: lanzamos un dado. Acharemos a probabilidade dos seguintes sucesos:
A = { 2, 4, 6} B = {3, 4} C = {2} E = {1, 2, 3, 4, 5, 6 }
A e B son sucesos compostos, C é un suceso elemental e E é o suceso seguro
O espazo mostral é E = { 1, 2, 3, 4, 5, 6}, polo tanto, hai seis casos posibles. Trátase dun espazo de casos equiprobables e podemos aplicar a regra de Laplace.
P [ A ] = ![]() P [ B ] =
P [ B ] = 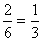 P [C ] =
P [C ] = 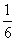 P [ E ] =
P [ E ] =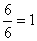
Este último suceso é o suceso seguro, e a súa probabilidade é 1.
Exemplo: dunha rifa vendéronse 1 000 papeletas numeradas do 1 ao 1 000. Cal é a probabilidade de que me toque si comprei unha papeleta? E se compro sete?
Loxicamente, todas as papeletas teñen a mesma probabilidade de saír. Se só compro unha papeleta, a probabilidade de gañar será:
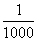
Se compramos sete papeletas teremos sete oportunidades entre mil de gañar, polo que a probabilidade será:
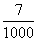
Os casos favorables son as papeletas compradas en cada caso, e os posibles son o total das papeletas da rifa.
Actividade resolta
Nunha bolsa que conten unha bóla branca e cen negras, sacamos unha ao chou.
a) Se B é o suceso sacar bóla branca e N sacar bóla negra, daquela o espazo de sucesos E ={ B,N } é un espazo de sucesos equiprobables?
b) Escriba un espazo mostral correspondente a esta experiencia aleatoria que estea formado por sucesos elementais equiprobables.
-
Solución
-
a) Evidente mente non, xa que temos máis bólas negras que brancas.
-
b) Se as bolas negras estivesen numeradas, e o espazo fose E = {B, N1, N2,N3………….N100}
-
Actividades propostas
S12. Indique en cada situación se é posible aplicar a regra de Laplace e en caso positivo, escriba o espazo mostral correspondente:
- Tirar unha chincheta sobre a mesa e observar se cae coa punta cara a arriba ou apoiada na punta e na cabeza.
- Extraer dúas bólas consecutivas dunha bolsa que conten dúas bólas brancas e unha negra.
S13. Un videoclube automático estragado reparte ao chou as películas entre os clientes. Se ten 30 infantís, 125 de acción, 200 dramas e 94 comedias. Cal é a probabilidade de que a película sexa comedia? E de que non sexa drama?
S14. Se consideramos un experimento que consiste en lanzar un dado dodecaédrico coas caras numeradas do 1 ao 12. Calcule as probabilidades seguintes:
|
Sacar un 3 |
Sacar un múltiplo de 3 |
Non sacar múltiplo de 3 |
Sacar número negativo |
Sacar menos de 20 |
S15. Lanzamos dous dados e sumamos as súas puntuacións. Pode realizar un cadro de dobre entrada para non esquecer ningún resultado.
 |
|
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0