2.1.6 Parámetros estatísticos. Cálculo e significado

Despois de obter os datos dunha distribución, necesitamos sintetizar a información para a súa posterior análise. Para iso, obteremos os parámetros estatísticos que serán de dous tipos: de centralización e de dispersión.

Parámetros de centralización

Indícannos en torno a que valor se distribúen os datos.

Parámetros de dispersión

Infórmannos sobre canto se afastan do centro os valores da distribución.

Medidas de centralización

Media

Se chamamos, x1, x2, ... xn aos valores que toma unha distribución estatística, a media ou termo medio, calculase así:

=

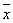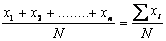
Mediana

Se ordenamos os datos da distribución de menos a maior, a mediana, Me, é o valor que se atopa no medio; é dicir, deixa tantos individuos antes, como despois. Se o número de datos fose par, á mediana asignáselle o valor medio dos dous termos centrais.

Moda	Este valor é o que máis frecuencia ten, e coñecémolo por Mo.

Estes valores son arredor dos que se distribúen todos os valores da distribución.

Cuartís

Os cuartís dunha serie estatística son Q1, Q2, e Q3, de tal xeito que: Q1 deixa á súa esquerda o 25 % dos datos. Q2 deixa á súa esquerda o 50 % dos datos e coincide coa mediana. Q3 deixa á súa esquerda o 75 % dos datos.

Medidas de dispersión

Veremos agora uns parámetros que serven para medir como de dispersos están os datos. En todos eles, o fundamental é medir o grao de separación dos datos con respecto á media.

Percorrido ou rango

É a diferenza entre o dato maior e o menor. Vén sedo a lonxitude do tramo dentro do cal están os datos.

Desviación media

Termo medio das distancias dos datos á media. Áchase coa media das diferenzas en valor absoluto.

Varianza

É o termo medio dos cadrados das distancias dos datos á media.

A varianza ten o problema de que as unidades en que se expresa ao estaren elevadas ao cadrado desvirtúan as medidas. Así, por exemplo, se estudamos as estatura, ao elevarmos ao cadrado as unidades serían cm², e isto non representa unha lonxitude, senón unha superficie. Por iso extraemos a súa raíz cadrada, é dicir a desviación típica.

Desviación típica

É a raíz cadrada da varianza.

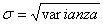
A partir de agora prestaremos especial atención aos parámetros, media () e desviación típica ().

Uso da calculadora

Para o cálculo destes parámetros podemos utilizar a calculadora, de pantalla sinxela ou descritiva, pero sempre unha calculadora científica e traballando en modo estatístico: mode SD.
Prepare a calculadora en modo SD Borre os datos anteriores: INV AC Introduza os datos, escribindo os valores e premendo a tecla DATA. Resultados (teclas): - n: dá o número de datos introducidos - 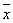: dá o valor da media. - 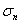: dá o valor da desviación típica.

Actividades resoltas

Xan foi anotando as temperaturas do seu pobo durante os sete días dunha semana:

19 Cº

21 Cº

19 Cº

18Cº

18 Cº

20 Cº

18Cº

• Que valores representan as temperaturas desa semana?

Solución

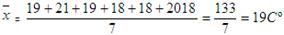
Calculamos a media:   Así que a media será 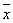= 19 Cº Calculamos a mediana: se ordenamos os datos de menos a maior teremos: 18, 18, 18,19, 19, 20, 21, así que o termo que deixa tantos elementos antes como despois é 19Cº Así que a medianaserá Me = 19 Cº Calculamos a moda: se observamos os datos vemos que 18 Cº é a temperatura que máis se repite. Así que a modaserá Mo = 18 Cº Calculamos os cuartís: Q1, Q2 e Q3. Q2 coincide coa mediana, polo que será 19 Cº. Q1 será o termo que deixe antes o 25 % dos valores

Dados os datos seguintes, ordenámolos nunha táboa de frecuencias e calculamos as medidas de centralización.

12

10

11

13

12

11

13

12

13

13

12

13

11

12

13

13

11

12

11

12

11

14

12

14

12

11

12

13

11

13

Solución

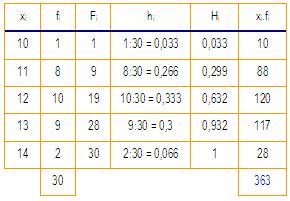
Faremos primeiro un reconto dos datos e ordenarémolos na táboa de frecuencias. Calculamos a media. Teremos que sumar os datos da variable e dividir polo numero total de datos, pero se nos fixamos nos datos, vemos que varios están repetidos, é dicir, a súa frecuencia absoluta é maior que 1, polo que resulta máis doado, multiplicar un determinado valor pola súa frecuencia. É máis doado facer 12 x 10, que sumar o valor 12 dez veces: aplicamos multiplicación en lugar da suma reiterada. Se nos fixamos na terceira columna, vén sendo esta operación. 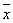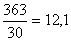Por tanto, a media quedará: =   Calculamos a moda. Será o valor que teña maior frecuencia, xa que isto quere dicir que é o valor que máis se repite. Xa que logo, a media será Mo = 12 Calculamos a mediana. Como neste caso temos un numero de datos par, será a media dos dous termos centrais, cando estes estean ordenados. Os dous son o 12. 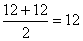Daquela, a mediana será: Me =  Esta información que ofrecen os parámetros de centralización dinos que estes datos están todos arredor do valor 12. Xorde, entón, a seguinte pregunta: se todos están arredor do valor 12, son todos próximos a 12? Esta pregunta ten sentido, se pensamos que para obtermos 12 de media podemos partir de 2 e 22 ou ben de 14 e 10. En ambos os casos a media é 12, pero os datos de partida son ben diferentes. Isto fai necesario coñecer máis sobre os datos da distribución, e para iso temos os parámetros de dispersión, que nos informarán de como están de aproximados os datos da táboa

 Obter as medidas de dispersión da seguinte distribución de notas:

2

4

4

4

5

7

9

9

10

Solución

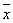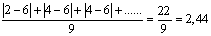
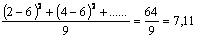
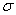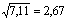
Percorrido ou rango : 10-2= 8 = 6 DM = Var = = Logo de obtermos os parámetros veremos o seu significado. Conxuntamente, a media e a desviación típica infórmannos de como están distribuídos os datos; neste caso como son as notas de partida. A media vale 6 e a desviación típica, 2,67. Isto dinos que entre 6 - 2,67 e 6 + 2,67, se atopa a maior parte das notas, arredor do 68 %, como se pode comprobar ollando os datos iniciais. O rango vale 8, e está a marcarnos o tipo de datos de partida; as notas están moi dispersas. Teremos en conta que para obter un 6 de media, podémolo facer cun 2 e un 10, pero tamén cun 7 e un 5; neste caso o percorrido sería 2, moito máis curto.