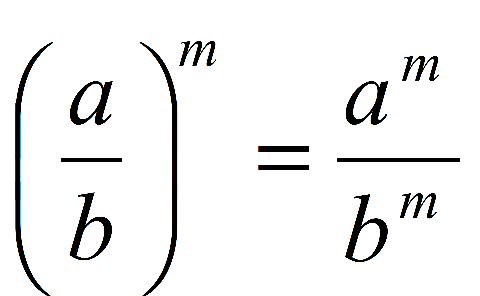Saltar navegación

2.2.1 Lembremos

Lembremos

  • Unha potencia é un produto de dous ou máis números iguais.

    a 4  = a x a x a x a

    a4

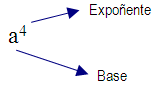
  • Potencia de expoñente 1 a1 = a

  • Potencia de expoñente 0 a 0 = 1

  • Propiedades das potencias de expoñente natural:

am · an = am+n

(a · b)m = am · bm

am · an = am – n

  

am

(am)n = am·n

 

  • Potencias de expoñente enteiro.

    • Temos que facer 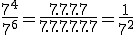\frac{7^4}{7^6}=\frac{7.7.7.7}{7.7.7.7.7.7}=\frac1{7^2} e, por outra banda, sabemos que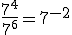  \frac{7^4}{7^6}=7^{-2}

Xa que logo, \frac1{7^2}=7^{-2} son resultados iguais.

Daquela, diremos que as potencias de expoñente negativo se definen como:

am, e as propiedades serán as mesmas que as anteriores.

    • Como expresariamos 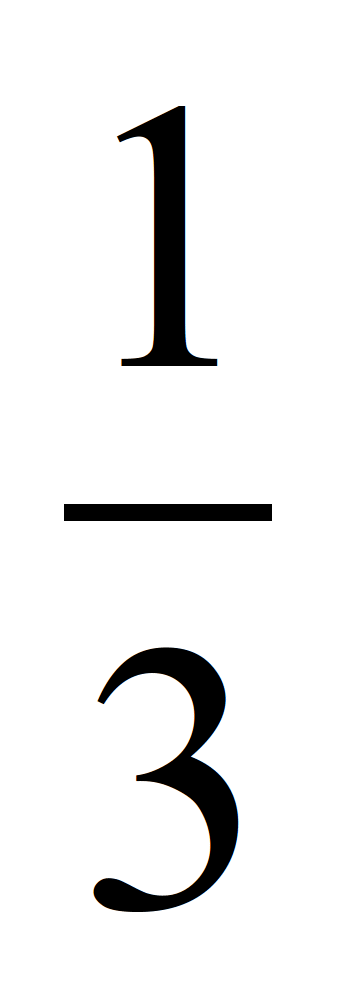13, tendo en conta o anterior?

Pois fariamos uso da definición para expresar   \frac13\;=\;3^{-1}, polo que o inverso dun numero enteiro será unha potencia de expoñente -1

  • Operacións que non se poden facer coas potencias.

Non se pode reducir, sen operar previamente, 22 + 52, nin tampouco 33 + 3-3.

22 + 52 ≠ 72
  • Compróbense as desigualdades seguintes:

(3 +4)2   ≠  32 + 42

(3 – 4)2  ≠   32 – 42

33 + 3-3  ≠  30

 

Actividade con solución.

Exprese como unha soa potencia:

 \frac1{2^5} .................. 13^{-2} imes\;4\;^{-2}
5^4 imes5^{-2} ..................  \left(7^2\right)^4
 7^4\div\;7^{-3} ...................  \frac17
 

Actividades propostas

S3. As medidas da sala do museo de Ciencias en metros son: 26 de longo, 25 de anchura e 23 de alto. Cal é o volume da sala?

S4. Se elevamos un numero ao cubo e o resultado ao cadrado, obtemos o mesmo resultado que se o elevamos ao cadrado e o resultado ao cubo?

S5. Exprese como unha soa potencia:

    • a)   33. 34. 3 =
    • b)   57. 53 =
    • c)   57 : 53 =
    • d )   ( 5 3) 4 =
    • e)   ( 5. 2. 3 ) 4 =

S6. Exprese como unha soa potencia:

 4

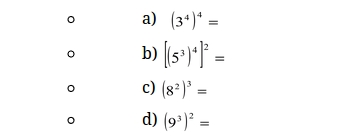
Licenciado baixo a Licenza Creative Commons Recoñecemento Non-comercial Compartir igual 3.0