Súmate a la fiesta
En vuestra fiesta no pueden faltar los zumos de frutas pero, revisa los cortes, si no son iguales no los podrás sumar.
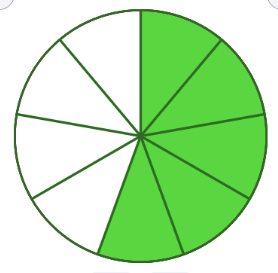
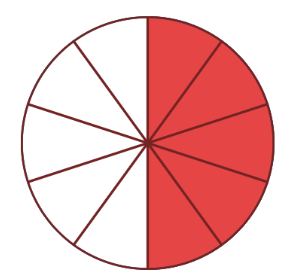
Partes iguales
Estas rodajas son cortes iguales, del mismo tamaño, se pueden sumar.


Para sumar fracciones también es necesario que los denominadores sean iguales.
Luego sumas los numeradores, ¡ya está!
Ejemplo: \(\dfrac{1}{8}+\dfrac{2}{8}= \dfrac{3}{8}\)
¿A que es fácil?
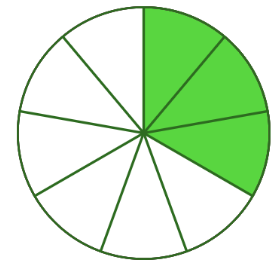
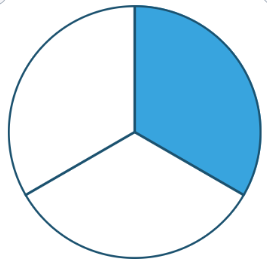
Partes distintas
Ahora has cortado trozos diferentes. ¡Uhm...! ¡No los puedes sumar!

 Entonces debes hacer fracciones equivalentes a cada una de ellas, buscando, además, que tengan el mismo denominador, como en el apartado 3.2.
Entonces debes hacer fracciones equivalentes a cada una de ellas, buscando, además, que tengan el mismo denominador, como en el apartado 3.2.
Tendrás que multiplicar cada fracción por un número.
¿Cómo saber cuál es el número?
Sigue leyendo...
Inspírate bajo el árbol
La solución está en la factorización, ¿recuerdas el árbol de factores? Úsalo.

 Buscar un denominador común es parecido a buscar un factor común.
Buscar un denominador común es parecido a buscar un factor común.
- Puedes lograrlo multiplicando los denominadores entre sí.
- También puedes hallar el m.c.m. de los denominadores.
Recuerda que para eso, debes factorizarlos.
Ejemplo 1
Por ejemplo: \(\dfrac{1}{4} + \dfrac{5}{6} = ?\) El denominador común es 4 x 6 = 24.
Para conseguirlo, multiplica el numerador y denominador de la primera fracción por 6 y el de la segunda por 4.
\(\dfrac{1 \times 6}{4 \times 6}+\dfrac{5 \times 4}{6 \times 4}\) = \(\dfrac{6}{24} + \dfrac{20}{24}\)
Y ya se pueden sumar; \(\dfrac{6}{24} + \dfrac{20}{24} = \dfrac{6 + 20}{24}=\dfrac{26}{24}=\dfrac{13}{12}\)
Ejemplo 2
Si prefieres utilizar el m.c.m. (4, 6) = 12
Observa que si pones un 12 en el denominador, habrás multiplicado por 3, en la primera fracción, y por 2 en la segunda.
\(\dfrac{1 \times 3}{4 \times 3}+\dfrac{5 \times 2}{6 \times 2}\) = \(\dfrac{3}{12} + \dfrac{10}{12}\)
Y ya se pueden sumar; \(\dfrac{3}{12} + \dfrac{10}{12} = \dfrac{3 + 10}{12}=\dfrac{13}{12}\)