El máximo común divisor de dos o más números es el mayor de sus divisores comunes.
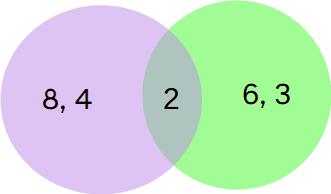
Por ejemplo, el máximo común divisor de 8 y 6 es 2, que es el mayor de los números que divide a ambos.
Divisores de 6 = {1, 2, 3, 6}
Divisores de 8 = {1, 2, 4, 8}
Observa que los divisores, también son factores.
El mínimo común múltiplo de dos o más números es el menor de sus múltiplos comunes.
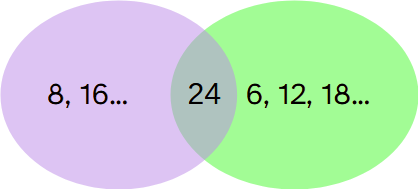Por ejemplo, el mínimo común múltiplo de 8 y 6 es 24, que es el menor de los múltiplos que de ambos.
Múltiplos de 6 = {6, 12, 18, 24...}
Múltiplos de 8 = {8, 16, 24...}
El primer múltiplo que coincide en ambos conjuntos es el 24.
Observa que los múltiplos de cada número se obtienen a partir de su tabla de multiplicar, y que son infinitos.
Para hallar el máximo común divisor y el mínimo común múltiplo de dos o más números, se puede utilizar la descomposición en factores primos de cada uno de ellos.
Recuerda que un número es primo si sólo es divisible por el mismo y la unidad.
Las calculadoras modernas tienen una tecla que hace esta factorización, mira a ver si la tuya la tiene.
Descomponer un número en factores primos consiste en expresarlo como una multiplicación de números primos.
La factorización prima es importante porque es única para cada número.
Ejemplo: la factorización prima de 20 es 20 = 2 x 2 x 5
Para encontrar esta factorización se van haciendo divisiones del número y el resultado (cociente) se vuelve a dividir hasta obtener un 1.
Hallar el mínimo común múltiplo (m.c.m.) de los números 18, 12 y 24 utilizando la descomposición en factores primos.
18 = 2 x 3 x 3 escribe los factores repetidos en forma de potencia: 18 = 2 x 32
12 = 2 x 2 x 3 escribe los factores repetidos en forma de potencia: 12 = 22 x 3
24 = 2 x 2 x 2 x 3 escribe los factores repetidos en forma de potencia: 24 = 23 x 3
Elige los factores "comunes y no comunes con mayor exponente": 23 x 32 = 72
El mínimo común múltiplo de 18, 12 y 24 es el número 72. m.c.m. (18, 12, 24) = 72.
Hallar el máximo común divisor (m.c.d.) de los números 18, 12 y 24, utilizando la descomposición en factores primos.
18 = 2 x 3 x 3 debemos expresarlo con potencias: 18 = 2 x 32
12 = 2 x 2 x 3 debemos expresarlo con potencias: 12 = 22 x 3
24 = 2 x 2 x 2 x 3 debemos expresarlo con potencias: 24 = 23 x 3
Elige los factores "comunes con menor exponente": 2 x 3 = 6
El máximo común divisor de 18, 12 y 24 es el número 6. m.c.d. (18, 12, 24) = 6.
Importante tener en cuenta que, si no hay factores comunes, su m.c.d. es 1, entonces se dice que son números primos entre sí.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0