Definición

Una fracción es el cociente de dos números enteros, llamados numerador y denominador.

El denominador nunca puede ser 0.

Ejemplos: \(\displaystyle\frac{1}{3}\) , \(\displaystyle\frac12\) , 2/5, 1/7 ...

Al trabajar con fracciones es importante identificar su valor, comparado con la unidad.

1. Fracciones propias: su numerador es menor o igual que el denominador (su valor menor es menor o igual que uno). Ejemplo: 3/4

2. Fracciones impropias: su numerador es mayor que el denominador (su valor es mayor que uno). Ejemplo: 7/4

 

Número mixto

Un número mixto es una forma de escribir una fracción impropia.

Se escribe separando la parte entera de la parte no entera.

La calculadora tiene esta forma de escritura, ya que es muy utilizada en países anglosajones.

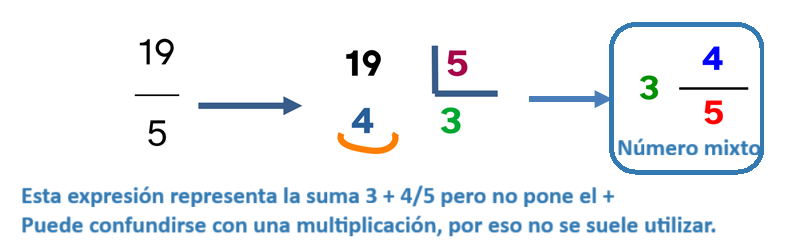
Para escribir una fracción en este formato, divide el numerador entre el denominador.

El cociente es la parte entera, y el resto es el nuevo numerador que se pone en la parte fraccionaria.

Comparación

I. Si tienen el mismo denominador, la fracción mayor es la de mayor numerador.

Ejemplo:

II. Si tienen distinto denominador, hay que hacer previamente algún cálculo.

• Una opción es buscar su valor decimal, dividiendo numerador entre denominador, y luego hacer la comparación.
• Otra opción es hacer un producto cruzado. Presta atención:

Si quieres saber por qué funciona, sigue leyendo...

¿Por qué?

Esta técnica consigue, de forma encubierta, igualar denominadores.

\(\displaystyle\frac{7}{4}\) , \(\displaystyle\frac{6}{3}\)

• Si multiplicas la primera por 3, tanto numerador como denominador obtienes: \(\displaystyle\frac{21}{12}\)
• Si multiplicas la segunda por 4, tanto numerador como denominador obtienes:  \(\displaystyle\frac{24}{12}\)

Ahora, con denominadores iguales, basta comparar los numeradores.

Puedes ver esto de forma gráfica en la siguiente actividad interactiva.