Saltar la navegación

3.4. Sabores en rodajas

¡Cuanto corte!

¿Pensaste alguna vez qué pasa si una rodaja la vuelves a partir? ¡Estás haciendo una fracción de una fracción!

Multiplica los cortes

Mira estas rodajas, la segunda es la mitad de la primera, que ya era parte de un limón.

Rodaja de limón Gajo de limónCuando multiplicas fracciones, haces este efecto, el de una "fracción de fracción".

Puedes quedarte con esta idea. "La mitad de la mitad, es la cuarta parte".

Ejemplo: \(\dfrac{1}{2}\times\dfrac{1}{2}= \dfrac{1}{4}\)

El resultado de multiplicar dos fracciones, es otra fracción con numerador el producto de los numeradores y el denominador el producto de los denominadores.

Ejemplo: \(\dfrac{2}{5}\times\dfrac{3}{4}\) = \(\dfrac{2 \times 3}{5 \times 4}\) = \(\dfrac{6}{20}\)

Recuerda que la multiplicación tiene la propiedad conmutativa, por eso puedes intercambiar los factores.

¿Y la división?

Dividir es la operación inversa de multiplicar, y en eso te vas a apoyar.

Caja de bombonesDividir una fracción entre otra, es lo mismo que multiplicar la primera por la inversa de la segunda.

Ejemplo: \(\dfrac{2}{5}÷\dfrac{3}{4}\) = \(\dfrac{2 \times 4}{5 \times 3}\) = \(\dfrac{8}{15}\)

Fíjate que hemos intercambiado el numerador y el denominador la segunda fracción (es su inversa).

Sorprende un poco que en la división el resultado sea mayor que el original.

Pero piensa que, si tienes que repartir bombones entre la mitad de personas, tocarán a más bombones

Enteros I

LimónA veces multiplicarás por un número que no está en forma de fracción.

Por ejemplo, cuando calculas porcentajes.

Si te piden hacer la mitad de 8, es lo mismo que 8 x \(\dfrac{1}{2}\) o también \(\dfrac{1}{2}\) x 8.

Puedes poner 8 como una fracción, añadiendo un 1 en el denominador.

Ejemplo: \(\dfrac{1}{2}\times\dfrac{8}{1}\) = \(\dfrac{1 \times 8}{2 \times 1}\) = \(\dfrac{8}{2}\) = 4

Enteros II

NaranjaPara la división se hace lo mismo, poner un uno debajo.

Ejemplo: \(\dfrac{2}{5}÷\dfrac{8}{1}\) = \(\dfrac{2 \times 1}{5 \times 8}\) = \(\dfrac{2}{40}\)

Si el valor entero está en primer lugar, se hace igual.

Ejemplo: \(\dfrac{8}{1}÷\dfrac{2}{5}\) = \(\dfrac{8 \times 5}{1 \times 2}\) = \(\dfrac{40}{2}\) =20

Multiplica la igualdad

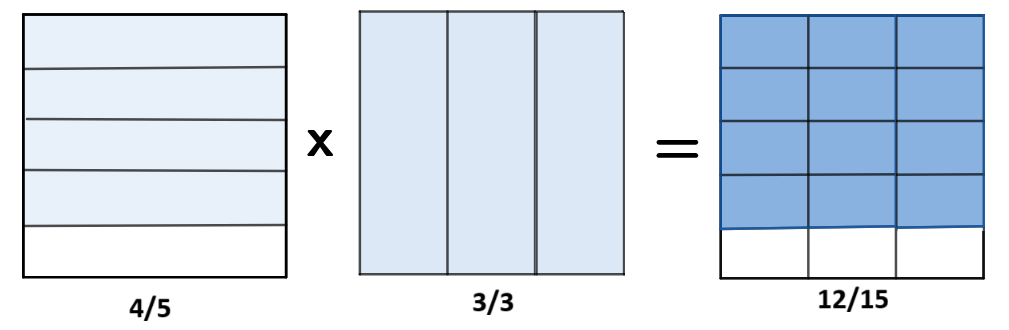Símbolo masculino igualado al femeninoRevisa las fracciones equivalentes...

También se hallan multiplicando.

En este caso por una fracción que vale 1.

No te cortes en la fiesta

Haz las siguientes multiplicaciones y divisiones. Escribe el resultado en la forma a/b.

\(\dfrac{2}{5}\times\dfrac{1}{8}\) =  \(\dfrac{9}{4}÷\dfrac{1}{8}\) = 
\(\dfrac{3}{10}\times\dfrac{2}{7}\) =  \(\dfrac{5}{6}÷\dfrac{1}{12}\) = 
\(\dfrac{7}{4}\times\dfrac{1}{10}\) =   \(\dfrac{2}{5}÷\dfrac{1}{8}\) = 
\(\dfrac{10}{6}\times\dfrac{3}{2}\) =   \(\dfrac{7}{4}÷\dfrac{1}{10}\) = 
\(\dfrac{9}{4}\times\dfrac{1}{8}\) =   \(\dfrac{3}{10}÷\dfrac{2}{7}\) =
\(\dfrac{1}{12}\times\dfrac{5}{6}\) =   \(\dfrac{10}{6}÷\dfrac{3}{2}\) =

Habilitar JavaScript

Distribuye la fruta

Organizando la fruta

En la frutería donde vais a comprar para la fiesta, han entrado 360 cajas de fruta, que se van a repartir de la siguiente forma:

Frutería

  • \(\dfrac{1}{4}\) para poner hoy a la venta.
  • La mitad de la que se pone a la venta tendrá un precio de oferta.
  • \(\dfrac{3}{5}\) Para guardar en la cámara a madurar.
  • \(\dfrac{3}{20}\) para enviar a obras sociales, repartidos de la siguiente forma: la tercera parte para Cáritas y los dos tercios restantes para la Cruz Roja.
  • Explica en forma de fracción y de número de cajas, el reparto según sus destinos.

Escribe los cálculos en tu cuaderno.

Soluciones guiadas

Tabla de distribución de la fruta.

    Reparto de las 360 cajas en fracciones y cantidades
    Destino Fracción (a/b) Cajas

    Venta

    repartido en:

    		 x 1/4 = 90 cajas, repartidas en:
     =  con oferta.

    360 x =  cajas.
     =  sin oferta.

    360 x =  cajas.

    Cámara

    		x 3/5 = cajas.

    Obras sociales

      repartido en:

    		 360 x 3/20 = cajas, repartidas en:

    3/20 x  = Cáritas.

    Simplificada es

    360 x = 18 cajas.

    (Utiliza la fracción simplificada)

    3/20 x    =  Cruz Roja.

    Simplificada es

    360 x = 36 cajas.

    (Utiliza la fracción simplificada)

    Habilitar JavaScript

    Practica cortes y recortes

    Elige la respuesta correcta.

    undefined

    %E9%B0%F3%E1%FB%F5%FC%F3%E6%E7%E0%F3%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%F3%E7%E6%FA%FD%E0%C4%FB%F6%F7%FD%B0%A8%B0%B0%BE%B0%E6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%C1%F7%FE%F7%F1%F1%FB%FD%FC%F3%B0%BE%B0%F7%FC%F6%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%FB%F6%C4%FB%F6%F7%FD%B0%A8%B0%B0%BE%B0%E1%E6%F3%E0%E6%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%FB%FC%E1%E6%E0%E7%F1%E6%FB%FD%FC%E1%D7%EA%F7%B0%A8%B0%B7%A1%D1%E2%B7%A1%D7%D7%FE%FB%F5%F7%B7%A0%A2%FE%F3%B7%A0%A2%E0%F7%E1%E2%E7%F7%E1%E6%F3%B7%A0%A2%F1%FD%E0%E0%F7%F1%E6%F3%BC%B7%A1%D1%BD%E2%B7%A1%D7%B0%BE%B0%FB%FC%E1%E6%E0%E7%F1%E6%FB%FD%FC%E1%B0%A8%B0%C1%F7%FE%F7%F1%F1%FB%FD%FC%F3%B2%FE%F3%E1%B2%E0%F7%E1%E2%E7%F7%E1%E6%F3%E1%B2%F1%FD%E0%E0%F7%F1%E6%F3%E1%B2%EB%B2%E2%E7%FE%E1%F3%B2%E1%FD%F0%E0%F7%B2%F7%FE%B2%F0%FD%E6a%FC%B2%CE%B0%E0%F7%E1%E2%FD%FC%F6%F7%E0%CE%B0%B2%B0%BE%B0%E1%FA%FD%E5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%FD%E2%E6%FB%FD%FC%E1%C0%F3%FF%F6%FD%FC%B0%A8%F4%F3%FE%E1%F7%BE%B0%F3%FC%E1%E5%F7%E0%E1%C0%F3%FF%F6%FD%FC%B0%A8%E6%E0%E7%F7%BE%B0%E1%FA%FD%E5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%E6%E0%E7%F7%BE%B0%E6%FB%FF%F7%C1%FA%FD%E5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%AB%BE%B0%E7%E1%F7%DE%FB%E4%F7%E1%B0%A8%E6%E0%E7%F7%BE%B0%FC%E7%FF%F0%F7%E0%DE%FB%E4%F7%E1%B0%A8%A1%BE%B0%FB%E6%FB%FC%F7%E0%F3%E0%EB%B0%A8%E9%B0%E1%FA%FD%E5%D1%FE%E7%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FE%E7%F7%D5%F3%FF%F7%B0%A8%B0%B0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F5%F7%D1%FE%E7%F7%B0%A8%A6%A2%BE%B0%E1%FA%FD%E5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%BE%B0%FF%F7%E1%E1%F3%F5%F7%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%EF%BE%B0%E1%F7%FE%F7%F1%E6%E1%D5%F3%FF%F7%B0%A8%C9%E9%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%E6%FB%FF%F7%B0%A8%A2%BE%B0%FC%E7%FF%F0%F7%E0%DD%E2%E6%FB%FD%FC%E1%B0%A8%A1%BE%B0%E6%EB%E2%F7%C1%F7%FE%F7%F1%E6%B0%A8%A2%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%F3%FE%E6%B0%A8%B0%D1%FD%E0%E6%F3%E0%B2%E2%F3%FC%B0%BE%B0%F1%E7%E1%E6%FD%FF%C1%F1%FD%E0%F7%B0%A8%A3%BE%B0%E7%E0%FE%B0%A8%B0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%F1%FD%E0%E6%F3%E0%CD%F7%FE%CD%E2%F3%FC%BC%E2%FC%F5%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%FA%FB%E6%B0%A8%BF%A3%BE%B0%F7%E0%E0%FD%E0%B0%A8%BF%A3%BE%B0%FF%E1%F5%DA%FB%E6%B0%A8%B0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%B0%A8%B0%B0%BE%B0%E1%FD%E7%FC%F6%C4%FB%F6%F7%FD%B0%A8%A3%BE%B0%FB%FF%F3%F5%F7%C4%FB%F6%F7%FD%B0%A8%A3%BE%B0%FB%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%F4%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%E1%FB%FE%F7%FC%E6%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%E6%C1%FB%FE%F7%FC%E6%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%F7%C6%F7%EA%E6%B0%A8%B0%B0%BE%B0%E3%E7%F7%EA%E6%FB%FD%FC%B0%A8%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A3%EF%E9%A0%EF%CE%CE%BB%B2%EA%B2%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A1%EF%E9%A6%EF%CE%CE%BB%B2%AF%B0%BE%B0%FD%E2%E6%FB%FD%FC%E1%B0%A8%C9%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A4%EF%E9%AA%EF%CE%CE%BB%B0%BE%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A1%EF%E9%AA%EF%CE%CE%BB%B0%BE%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A3%EF%E9%A0%EF%CE%CE%BB%B0%BE%B0%B0%CF%BE%B0%E1%FD%FE%E7%E6%FB%FD%FC%B0%A8%B0%D0%B0%BE%B0%E1%FD%FE%E7%E6%FB%FD%FC%C3%E7%F7%E1%E6%FB%FD%FC%B0%A8%B0%B0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F5%F7%C1%FA%FD%E5%B0%A8%A1%A7%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%E6%FB%FF%F7%B0%A8%A2%BE%B0%FC%E7%FF%F0%F7%E0%DD%E2%E6%FB%FD%FC%E1%B0%A8%A0%BE%B0%E6%EB%E2%F7%C1%F7%FE%F7%F1%E6%B0%A8%A2%BE%B0%EA%B0%A8%A2%BC%A7%AB%A6%AA%AB%A5%A1%A4%A0%A3%AA%A5%A6%A2%A0%AB%BE%B0%EB%B0%A8%A2%BC%A5%AB%AB%A3%AB%A5%A4%A4%A6%A3%A7%A3%AA%A0%A6%AB%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%F3%FE%E6%B0%A8%B0%D1%FD%E0%E6%F3%E0%B2%F7%FE%B2%E2%F3%FC%B0%BE%B0%F1%E7%E1%E6%FD%FF%C1%F1%FD%E0%F7%B0%A8%A3%BE%B0%E7%E0%FE%B0%A8%B0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%F1%FD%E0%E6%F3%E0%CD%F7%FE%CD%E2%F3%FC%BA%A3%BB%BC%E2%FC%F5%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%FA%FB%E6%B0%A8%BF%A3%BE%B0%F7%E0%E0%FD%E0%B0%A8%BF%A3%BE%B0%FF%E1%F5%DA%FB%E6%B0%A8%B0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%B0%A8%B0%B0%BE%B0%E1%FD%E7%FC%F6%C4%FB%F6%F7%FD%B0%A8%A3%BE%B0%FB%FF%F3%F5%F7%C4%FB%F6%F7%FD%B0%A8%A3%BE%B0%FB%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%F4%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%E1%FB%FE%F7%FC%E6%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%E6%C1%FB%FE%F7%FC%E6%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%F7%C6%F7%EA%E6%B0%A8%B0%B0%BE%B0%E3%E7%F7%EA%E6%FB%FD%FC%B0%A8%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A1%EF%E9%AA%EF%CE%CE%BB%B2e%B2%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A0%EF%E9%A6%EF%CE%CE%BB%B2%F7%E1%B2%FE%FD%B2%FF%FB%E1%FF%FD%B2%E3%E7%F7%BC%BC%BC%B0%BE%B0%FD%E2%E6%FB%FD%FC%E1%B0%A8%C9%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A1%EF%E9%AA%EF%CE%CE%BB%B2%EA%B2%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A0%EF%E9%A6%EF%CE%CE%BB%B0%BE%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A1%EF%E9%AA%EF%CE%CE%BB%B2%EA%B2%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A6%EF%E9%A0%EF%CE%CE%BB%B0%BE%B0%B0%BE%B0%B0%CF%BE%B0%E1%FD%FE%E7%E6%FB%FD%FC%B0%A8%B0%D0%B0%BE%B0%E1%FD%FE%E7%E6%FB%FD%FC%C3%E7%F7%E1%E6%FB%FD%FC%B0%A8%B0%B0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F5%F7%C1%FA%FD%E5%B0%A8%A1%A7%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%E6%FB%FF%F7%B0%A8%A2%BE%B0%FC%E7%FF%F0%F7%E0%DD%E2%E6%FB%FD%FC%E1%B0%A8%A0%BE%B0%E6%EB%E2%F7%C1%F7%FE%F7%F1%E6%B0%A8%A2%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%F3%FE%E6%B0%A8%B0%D1%FD%E0%E6%F3%E0%B2%E6%F3%E0%E6%F3%B2%F6%F7%B2%FF%F3%FC%E8%F3%FC%F3%B0%BE%B0%F1%E7%E1%E6%FD%FF%C1%F1%FD%E0%F7%B0%A8%A3%BE%B0%E7%E0%FE%B0%A8%B0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%F1%E7%F3%F6%E0%F3%F6%FB%E6%FD%E1%CD%F6%F7%CD%FF%F3%FC%E8%F3%FC%F3%BC%E2%FC%F5%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%FA%FB%E6%B0%A8%BF%A3%BE%B0%F7%E0%E0%FD%E0%B0%A8%BF%A3%BE%B0%FF%E1%F5%DA%FB%E6%B0%A8%B0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%B0%A8%B0%B0%BE%B0%E1%FD%E7%FC%F6%C4%FB%F6%F7%FD%B0%A8%A3%BE%B0%FB%FF%F3%F5%F7%C4%FB%F6%F7%FD%B0%A8%A3%BE%B0%FB%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%F4%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%E1%FB%FE%F7%FC%E6%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%E6%C1%FB%FE%F7%FC%E6%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%F7%C6%F7%EA%E6%B0%A8%B0%B0%BE%B0%E3%E7%F7%EA%E6%FB%FD%FC%B0%A8%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A1%EF%E9%A6%EF%CE%CE%BB%B2%F7%FC%E6%E0%F7%B2%E7%FC%B2%FF%F7%F6%FB%FD%B2%F7%E1%B2%FB%F5%E7%F3%FE%B2%F3%BC%BC%BC%B0%BE%B0%FD%E2%E6%FB%FD%FC%E1%B0%A8%C9%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A1%EF%E9%A0%EF%CE%CE%BB%B0%BE%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A4%EF%E9%A6%EF%CE%CE%BB%B0%BE%B0%B0%BE%B0%B0%CF%BE%B0%E1%FD%FE%E7%E6%FB%FD%FC%B0%A8%B0%D0%B0%BE%B0%E1%FD%FE%E7%E6%FB%FD%FC%C3%E7%F7%E1%E6%FB%FD%FC%B0%A8%B0%B0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F5%F7%C1%FA%FD%E5%B0%A8%A1%A7%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%E6%FB%FF%F7%B0%A8%A2%BE%B0%FC%E7%FF%F0%F7%E0%DD%E2%E6%FB%FD%FC%E1%B0%A8%A0%BE%B0%E6%EB%E2%F7%C1%F7%FE%F7%F1%E6%B0%A8%A2%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%F3%FE%E6%B0%A8%B0%D0%F3%E0%E0%F3%B2%F1%FD%FC%B2%E1%F3%F0%FD%E0%F7%E1%B2%F6%F7%B2%FA%F7%FE%F3%F6%FD%E1%B0%BE%B0%F1%E7%E1%E6%FD%FF%C1%F1%FD%E0%F7%B0%A8%A3%BE%B0%E7%E0%FE%B0%A8%B0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%F0%F3%E0%E0%F3%CD%F6%F7%CD%FA%F7%FE%F3%F6%FD%BC%E2%FC%F5%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%FA%FB%E6%B0%A8%BF%A3%BE%B0%F7%E0%E0%FD%E0%B0%A8%BF%A3%BE%B0%FF%E1%F5%DA%FB%E6%B0%A8%B0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%B0%A8%B0%B0%BE%B0%E1%FD%E7%FC%F6%C4%FB%F6%F7%FD%B0%A8%A3%BE%B0%FB%FF%F3%F5%F7%C4%FB%F6%F7%FD%B0%A8%A3%BE%B0%FB%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%F4%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%E1%FB%FE%F7%FC%E6%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%E6%C1%FB%FE%F7%FC%E6%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%F7%C6%F7%EA%E6%B0%A8%B0%B0%BE%B0%E3%E7%F7%EA%E6%FB%FD%FC%B0%A8%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A0%EF%E9%A6%EF%CE%CE%BB%B2%EA%B2%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A3%EF%E9%A0%EF%CE%CE%BB%B2%F7%E1%B2%FB%F5%E7%F3%FE%B2%F3%BC%BC%BC%B0%BE%B0%FD%E2%E6%FB%FD%FC%E1%B0%A8%C9%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A6%EF%E9%AA%EF%CE%CE%BB%B0%BE%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A0%EF%E9%AA%EF%CE%CE%BB%B0%BE%B0%B0%BE%B0%B0%CF%BE%B0%E1%FD%FE%E7%E6%FB%FD%FC%B0%A8%B0%D0%B0%BE%B0%E1%FD%FE%E7%E6%FB%FD%FC%C3%E7%F7%E1%E6%FB%FD%FC%B0%A8%B0%B0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F5%F7%C1%FA%FD%E5%B0%A8%A1%A7%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%E6%FB%FF%F7%B0%A8%A2%BE%B0%FC%E7%FF%F0%F7%E0%DD%E2%E6%FB%FD%FC%E1%B0%A8%A0%BE%B0%E6%EB%E2%F7%C1%F7%FE%F7%F1%E6%B0%A8%A2%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%F3%FE%E6%B0%A8%B0%C0%FD%F6%F3%F8%F3%B2%F6%F7%B2%E6%FD%FF%F3%E6%F7%B0%BE%B0%F1%E7%E1%E6%FD%FF%C1%F1%FD%E0%F7%B0%A8%A3%BE%B0%E7%E0%FE%B0%A8%B0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%E0%FD%F6%F3%F8%F3%CD%F6%F7%CD%E6%FD%FF%F3%E6%F7%BA%A3%BB%BC%E2%FC%F5%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%FA%FB%E6%B0%A8%BF%A3%BE%B0%F7%E0%E0%FD%E0%B0%A8%BF%A3%BE%B0%FF%E1%F5%DA%FB%E6%B0%A8%B0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%B0%A8%B0%B0%BE%B0%E1%FD%E7%FC%F6%C4%FB%F6%F7%FD%B0%A8%A3%BE%B0%FB%FF%F3%F5%F7%C4%FB%F6%F7%FD%B0%A8%A3%BE%B0%FB%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%F4%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%E1%FB%FE%F7%FC%E6%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%E6%C1%FB%FE%F7%FC%E6%C4%FB%F6%F7%FD%B0%A8%A2%BE%B0%F7%C6%F7%EA%E6%B0%A8%B0%B0%BE%B0%E3%E7%F7%EA%E6%FB%FD%FC%B0%A8%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A1%EF%E9%AB%EF%CE%CE%BB%B2%F7%FC%E6%E0%F7%B2%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A0%EF%E9%A1%EF%CE%CE%BB%B2%F7%E1%B2%FB%F5%E7%F3%FE%B2%F3%BC%BC%BC%B0%BE%B0%FD%E2%E6%FB%FD%FC%E1%B0%A8%C9%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%AB%EF%E9%A3%AA%EF%CE%CE%BB%B0%BE%B0%CE%CE%BA%CE%CE%F6%F4%E0%F3%F1%E9%A4%EF%E9%A0%A5%EF%CE%CE%BB%B0%BE%B0%B0%BE%B0%B0%CF%BE%B0%E1%FD%FE%E7%E6%FB%FD%FC%B0%A8%B0%D3%B0%BE%B0%E1%FD%FE%E7%E6%FB%FD%FC%C3%E7%F7%E1%E6%FB%FD%FC%B0%A8%B0%B0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F5%F7%C1%FA%FD%E5%B0%A8%A1%A7%EF%CF%BE%B0%FB%E1%C1%F1%FD%E0%FF%B0%A8%A3%BE%B0%E6%F7%EA%E6%D0%E7%E6%E6%FD%FC%C1%F1%FD%E0%FF%B0%A8%B0%D5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%E0%F7%E2%F7%F3%E6%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%E6%E0%E7%F7%BE%B0%E6%FB%E6%FE%F7%B0%A8%B0%B0%BE%B0%F1%E7%E1%E6%FD%FF%C1%F1%FD%E0%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%E6%F7%EA%E6%D3%F4%E6%F7%E0%B0%A8%B0%B7%A1%D1%E2%B7%A1%D7%B7%A1%D1%BD%E2%B7%A1%D7%B7%A2%D3%B7%A1%D1%F6%FB%E4%B7%A0%A2%FB%F6%B7%A1%D6%B7%A0%A0%E6%FD%FD%FE%E6%FB%E2%BF%E6%F3%F5%BF%E2%A2%D3%A4%A7%E3%AB%A7%B7%A0%A0%B7%A1%D7%B7%A1%D1%BD%F6%FB%E4%B7%A1%D7%B7%A2%D3%B7%A1%D1%F6%FB%E4%B7%A0%A2%FB%F6%B7%A1%D6%B7%A0%A0%E5%FB%F6%F5%F7%E6%BF%E2%A2%D3%A4%A7%E3%AB%A7%B7%A0%A0%B7%A1%D7%B7%A2%D3%B7%A1%D1%F6%FB%E4%B7%A0%A2%F1%FE%F3%E1%E1%B7%A1%D6%B7%A0%A0%E6%E6%E1%BF%E2%E0%F7%E4%FB%FD%E7%E1%B7%A0%A2%E6%E6%E1%BF%F0%E6%FC%B7%A0%A2%E5%FB%F6%F5%F7%E6%BF%FB%F1%FD%FC%B7%A0%A0%B7%A1%D7%B7%A1%D1%BD%F6%FB%E4%B7%A1%D7%B7%A2%D3%B7%A1%D1%F6%FB%E4%B7%A0%A2%F1%FE%F3%E1%E1%B7%A1%D6%B7%A0%A0%E6%E6%E1%BF%E2%FE%F3%EB%B7%A0%A2%E6%E6%E1%BF%F0%E6%FC%B7%A0%A2%E5%FB%F6%F5%F7%E6%BF%FB%F1%FD%FC%B7%A0%A0%B7%A1%D7%B7%A1%D1%BD%F6%FB%E4%B7%A1%D7%B7%A2%D3%B7%A1%D1%F6%FB%E4%B7%A0%A2%F1%FE%F3%E1%E1%B7%A1%D6%B7%A0%A0%E6%E6%E1%BF%E2%F3%E7%E1%F7%B7%A0%A2%E6%E6%E1%BF%F0%E6%FC%B7%A0%A2%E5%FB%F6%F5%F7%E6%BF%FB%F1%FD%FC%B7%A0%A0%B7%A1%D7%B7%A1%D1%BD%F6%FB%E4%B7%A1%D7%B7%A2%D3%B7%A1%D1%F6%FB%E4%B7%A0%A2%F1%FE%F3%E1%E1%B7%A1%D6%B7%A0%A0%E6%E6%E1%BF%E1%E6%FD%E2%B7%A0%A2%E6%E6%E1%BF%F0%E6%FC%B7%A0%A2%E5%FB%F6%F5%F7%E6%BF%FB%F1%FD%FC%B7%A0%A0%B7%A1%D7%B7%A1%D1%BD%F6%FB%E4%B7%A1%D7%B7%A2%D3%B7%A1%D1%F6%FB%E4%B7%A0%A2%F1%FE%F3%E1%E1%B7%A1%D6%B7%A0%A0%E6%E6%E1%BF%FC%F7%EA%E6%B7%A0%A2%E6%E6%E1%BF%F0%E6%FC%B7%A0%A2%E5%FB%F6%F5%F7%E6%BF%FB%F1%FD%FC%B7%A0%A0%B7%A1%D7%B7%A1%D1%BD%F6%FB%E4%B7%A1%D7%B7%A2%D3%B7%A1%D1%BD%F6%FB%E4%B7%A1%D7%B0%BE%B0%E6%F7%EA%E6%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%B7%A1%D1%E2%B7%A1%D7%B7%A1%D1%BD%E2%B7%A1%D7%B7%A2%D3%B7%A1%D1%F6%FB%E4%B7%A0%A2%FB%F6%B7%A1%D6%B7%A0%A0%E6%FD%FD%FE%E6%FB%E2%BF%E6%F3%F5%BF%E2%A2%D3%A4%A7%E3%AB%A7%B7%A0%A0%B7%A1%D7%B7%A1%D1%BD%F6%FB%E4%B7%A1%D7%B7%A2%D3%B7%A1%D1%F6%FB%E4%B7%A0%A2%FB%F6%B7%A1%D6%B7%A0%A0%E5%FB%F6%F5%F7%E6%BF%E2%A2%D3%A4%A7%E3%AB%A7%B7%A0%A0%B7%A1%D7%B7%A2%D3%B7%A1%D1%F6%FB%E4%B7%A0%A2%F1%FE%F3%E1%E1%B7%A1%D6%B7%A0%A0%E6%E6%E1%BF%E2%E0%F7%E4%FB%FD%E7%E1%B7%A0%A2%E6%E6%E1%BF%F0%E6%FC%B7%A0%A2%E5%FB%F6%F5%F7%E6%BF%FB%F1%FD%FC%B7%A0%A0%B7%A1%D7%B7%A1%D1%BD%F6%FB%E4%B7%A1%D7%B7%A2%D3%B7%A1%D1%F6%FB%E4%B7%A0%A2%F1%FE%F3%E1%E1%B7%A1%D6%B7%A0%A0%E6%E6%E1%BF%E2%FE%F3%EB%B7%A0%A2%E6%E6%E1%BF%F0%E6%FC%B7%A0%A2%E5%FB%F6%F5%F7%E6%BF%FB%F1%FD%FC%B7%A0%A0%B7%A1%D7%B7%A1%D1%BD%F6%FB%E4%B7%A1%D7%B7%A2%D3%B7%A1%D1%F6%FB%E4%B7%A0%A2%F1%FE%F3%E1%E1%B7%A1%D6%B7%A0%A0%E6%E6%E1%BF%E2%F3%E7%E1%F7%B7%A0%A2%E6%E6%E1%BF%F0%E6%FC%B7%A0%A2%E5%FB%F6%F5%F7%E6%BF%FB%F1%FD%FC%B7%A0%A0%B7%A1%D7%B7%A1%D1%BD%F6%FB%E4%B7%A1%D7%B7%A2%D3%B7%A1%D1%F6%FB%E4%B7%A0%A2%F1%FE%F3%E1%E1%B7%A1%D6%B7%A0%A0%E6%E6%E1%BF%E1%E6%FD%E2%B7%A0%A2%E6%E6%E1%BF%F0%E6%FC%B7%A0%A2%E5%FB%F6%F5%F7%E6%BF%FB%F1%FD%FC%B7%A0%A0%B7%A1%D7%B7%A1%D1%BD%F6%FB%E4%B7%A1%D7%B7%A2%D3%B7%A1%D1%F6%FB%E4%B7%A0%A2%F1%FE%F3%E1%E1%B7%A1%D6%B7%A0%A0%E6%E6%E1%BF%FC%F7%EA%E6%B7%A0%A2%E6%E6%E1%BF%F0%E6%FC%B7%A0%A2%E5%FB%F6%F5%F7%E6%BF%FB%F1%FD%FC%B7%A0%A0%B7%A1%D7%B7%A1%D1%BD%F6%FB%E4%B7%A1%D7%B7%A2%D3%B7%A1%D1%BD%F6%FB%E4%B7%A1%D7%B0%BE%B0%F5%F3%FF%F7%DF%FD%F6%F7%B0%A8%A3%BE%B0%F4%F7%F7%F6%D0%F3%F1%F9%B0%A8%F4%F3%FE%E1%F7%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F8%F7%D4%D0%B0%A8%A3%A2%A2%BE%B0%FD%E0%F6%F7%E0%B0%A8%A3%BE%B0%F1%E7%E1%E6%FD%FF%DF%F7%E1%E1%F3%F5%F7%E1%B0%A8%F4%F3%FE%E1%F7%BE%B0%E4%F7%E0%E1%FB%FD%FC%B0%A8%A1%BC%A3%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F8%F7%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%A3%A2%A2%BE%B0%F3%E7%F6%FB%FD%D4%F7%F7%F6%D0%F3%F1%FA%B0%A8%F4%F3%FE%E1%F7%BE%B0%FF%FD%F6%F7%D0%FD%F3%E0%F6%B0%A8%E6%E0%E7%F7%BE%B0%F7%E4%F3%FE%E7%F3%E6%FB%FD%FC%B0%A8%F4%F3%FE%E1%F7%BE%B0%F7%E4%F3%FE%E7%F3%E6%FB%FD%FC%DB%D6%B0%A8%B0%B0%BE%B0%FB%F6%B0%A8%B0%A0%A2%A0%A7%A6%A0%A0%AA%A1%AA%A1%A7%BF%A3%A0%A2%B0%BE%B0%FF%E1%F5%E1%B0%A8%E9%B0%FF%E1%F5%C0%F7%F3%F6%EB%B0%A8%B0-%C2%E0%F7%E2%F3%E0%F3%F6%FD%AD%B0%BE%B0%FF%E1%F5%C1%E6%F3%E0%E6%D5%F3%FF%F7%B0%A8%B0%C2%E7%FE%E1%F7%B2%F3%E3%E7%7F%B2%E2%F3%E0%F3%B2%F1%FD%FF%F7%E8%F3%E0%B0%BE%B0%FF%E1%F5%C1%E7%F0%FF%FB%E6%B0%A8%B0%D7%FC%E4%FB%F3%E0%B0%BE%B0%FF%E1%F5%D7%FC%E6%F7%E0%D1%FD%F6%F7%B0%A8%B0%DB%FC%E6%E0%FD%F6%E7%E8%F1%F3%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%D1%FD%F6%F7%B0%A8%B0%DD%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B2%FC%FD%FC%B2%7B%B2%F1%FD%E0%E0%F7%F1%E6%FD%B0%BE%B0%FF%E1%F5%D5%F3%FF%F7%DD%E4%F7%E0%B0%A8%B03%D4%FB%FC%B2%F6%F7%B2%FE%F3%B2%E2%F3%E0%E6%FB%F6%F3%B3%B0%BE%B0%FF%E1%F5%D1%FE%E7%F7%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B2%DE%F3%B2%E2%FB%E1%E6%F3%B2%F7%E1%A8%B0%BE%B0%FF%E1%F5%DC%F7%E5%D5%F3%FF%F7%B0%A8%B0%C2%E7%FE%E1%F7%B2%F3%E3%E7%7F%B2%E2%F3%E0%F3%B2%F1%FD%FF%F7%FC%E8%F3%E0%B2%FD%E6%E0%F3%B2%E2%F3%E0%E6%FB%F6%F3%B0%BE%B0%FF%E1%F5%CB%FD%E7%DA%F3%E1%B0%A8%B0%C6%FB%F7%FC%F7%B2%B7%A3%B2%F3%F1%FB%F7%E0%E6%FD%E1%B2%EB%B2%B7%A0%B2%F4%F3%FE%FE%FD%E1%B0%BE%B0%FF%E1%F5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%D1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%D3%F5%F3%FB%FC%B0%A8%B0%D8%E7%F5%F3%E0%B2%FD%E6%E0%F3%B2%E4%F7%E8%B0%BE%B0%FF%E1%F5%C0%F7%E3%E7%FB%E0%F7%F6%D3%F1%F1%F7%E1%E1%D9%F7%EB%B0%A8%B0%D7%E1%B2%FC%F7%F1%F7%E1%F3%E0%FB%FD%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%DE%FD%FD%F9%FB%FC%F5%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B2%DE%F3%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B2%E3%E7%F7%B2%F7%E1%E6%F3%F0%F3%B2%F0%E7%E1%F1%F3%FC%F6%FD%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%E6%F3%E0%E6%B0%A8%B0%C2%E7%FE%E1%F7%B2%F3%E3%E7%7F%B2%E2%F3%E0%F3%B2%F8%E7%F5%F3%E0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%E1%B0%A8%B0%D7%E0%E0%FD%E0%F7%E1%B0%BE%B0%FF%E1%F5%DA%FB%E6%E1%B0%A8%B0%D3%F1%FB%F7%E0%E6%FD%E1%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%B0%DF%FB%FC%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%DF%F3%EA%FB%FF%FB%E8%F7%B0%A8%B0%DF%F3%EA%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%C6%FB%FF%F7%B0%A8%B0%C6%FB%F7%FF%E2%FD%B2%E2%FD%E0%B2%E2%E0%F7%F5%E7%FC%E6%F3%B0%BE%B0%FF%E1%F5%DE%FB%E4%F7%B0%A8%B0%C4%FB%F6%F3%B0%BE%B0%FF%E1%F5%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C2%F3%FC%E6%F3%FE%FE%F3%B2%D1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%D7%EA%FB%E6%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C1%F3%FE%FB%E0%B2%F6%F7%FE%B2%FF%FD%F6%FD%B2%E2%F3%FC%E6%F3%FE%FE%F3%B2%F1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%DC%E7%FF%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%B0%DCh%FF%F7%E0%FD%B2%F6%F7%B2%E2%E0%F7%F5%E7%FC%E6%F3%E1%B0%BE%B0%FF%E1%F5%DC%FD%DB%FF%F3%F5%F7%B0%A8%B0%C2%E0%F7%F5%E7%FC%E6%F3%B2%E1%FB%FC%B2%FB%FFs%F5%F7%FC%F7%E1%B0%BE%B0%FF%E1%F5%D1%FD%FD%FE%B0%A8%B03%D0%FB%F7%FC%B3%B0%BE%B0%FF%E1%F5%DE%FD%E1%F7%C6%B0%A8%B0%DA%F3%E1%B2%E2%F7%E0%F6%FB%F6%FD%B2%A1%A1%A2%B2%E2%E7%FC%E6%FD%E1%B0%BE%B0%FF%E1%F5%DE%FD%E1%F7%DE%FB%E4%F7%B0%A8%B0%DA%F3%E1%B2%E2%F7%E0%F6%FB%F6%FD%B2%E7%FC%F3%B2%E4%FB%F6%F3%B0%BE%B0%FF%E1%F5%DE%FD%E1%E6%DE%FB%E4%F7%E1%B0%A8%B03%DA%F3%B2%E2%F7%E0%F6%FB%F6%FD%B2%E6%FD%F6%F3%E1%B2%E1%E7%E1%B2%E4%FB%F6%F3%E1%B3%B0%BE%B0%FF%E1%F5%D3%FE%FE%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%B03%D1%FD%FF%E2%FE%F7%E6%F3%F6%F3%E1%B2%FE%F3%E1%B2%E2%E0%F7%F5%E7%FC%E6%F3%E1%B3%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F7%E1%B0%A8%B0%D1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B2%D7%EA%F1%F7%FE%F7%FC%E6%F7%B3%B2%EE%B2%CA%F7%FC%FB%F3%FE%B3%B2%EE%B2%DF%FD%FB%B2%F0%F7%FC%B3%B2%EE%B2%C2%F7%E0%F4%F7%F1%E6%FD%B3%B0%BE%B0%FF%E1%F5%D4%F3%FB%FE%E7%E0%F7%E1%B0%A8%B03%DC%FD%B2%F7%E0%F3%B2%F7%E1%FD%B3%B2%EE%B23%DB%FC%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DE%FD%B2%E1%F7%FC%E6%FB%FF%FD%E1%B3%B2%EE%B23%D7%E0%E0%FD%E0%B3%B0%BE%B0%FF%E1%F5%DC%FD%E6%DC%F7%E6%E5%FD%E0%F9%B0%A8%B0%D3%B2%F7%E1%E6%F7%B2%F8%E7%F7%F5%FD%B2%E1a%FE%FD%B2%E1%F7%B2%E2%E7%F7%F6%F7%B2%F8%E7%F5%F3%E0%B2%F1%FD%FC%B2%F1%FD%FC%F7%EA%FBa%FC%B2%F3%B2%FB%FC%E6%F7%E0%FC%F7%E6%BC%B0%BE%B0%FF%E1%F5%D7%FC%F6%D5%F3%FF%F7%C1%F1%FD%E0%F7%B0%A8%B0%DB%FC%FB%F1%FB%F3%B2%F7%FE%B2%F8%E7%F7%F5%FD%BC%BC%BC%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%C1%F1%FD%E0%FF%B0%A8%B0%DE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%FC%FD%B2%E1%F7%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%E2%FD%E0%E3%E7%F7%B2%F7%E1%E6%F3%B2%E2s%F5%E7%FC%F3%B2%FC%FD%B2%B2%F4%FD%E0%FF%F3%B2%E2%F3%E0%E6%F7%B2%F6%F7%B2%E7%FC%B2%E2%F3%E3%E7%F7%E6%F7%B2%C1%D1%DD%C0%DF%BC%B0%BE%B0%FF%E1%F5%C3%E7%F7%E1%E6%FB%FD%FC%B0%A8%B0%C2%E0%F7%F5%E7%FC%E6%F3%B0%BE%B0%FF%E1%F5%D3%FC%E1%E5%F7%E0%B0%A8%B0%D1%FD%FF%E2%E0%FD%F0%F3%E0%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%C1%F1%FD%E0%F7%B0%A8%B03%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E7%FC%F3%B2%E4%F7%E8%B3%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%B0%A8%B0%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%B0%BE%B0%FF%E1%F5%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%B0%A8%B0%DB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%CB%FD%E7%C1%F1%FD%E0%F7%B0%A8%B0%C1%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%D3%E7%E6%FA%FD%E0%B0%A8%B0%D3%E7%E6%FD%E0%7F%F3%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C1%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%BC%B2%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F8%E7%F5%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%BC%B0%BE%B0%FF%E1%F5%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C1%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F3%E7%E6%FD%FFs%E6%FB%F1%F3%FF%F7%FC%E6%F7%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%B0%BE%B0%FF%E1%F5%C1%F7%E4%F7%E0%F3%FE%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E6%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%F1%FD%FF%FD%B2%E3%E7%FB%F7%E0%F3%B0%BE%B0%FF%E1%F5%CB%FD%E7%DE%F3%E1%E6%C1%F1%FD%E0%F7%B0%A8%B0%D3%B2h%FE%E6%FB%FF%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F5%F3%E0%F6%F3%F6%F3%B2%7B%B0%BE%B0%FF%E1%F5%D3%F1%E6%FB%E6%EB%D1%FD%FF%E2%FE%EB%B0%A8%B0%CB%F3%B2%FA%F3%B2%E0%F7%F3%FE%FB%E8%F3%F6%FD%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%BC%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%F7%E4%F7%E0%F3%FE%C6%FB%FF%F7%E1%B0%A8%B0%C2%FD%F6%F7%B2%E0%F7%F3%FE%FB%E8%F3%E0%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%F7%B2%E6%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%F1%FD%FF%FD%B2%E3%E7%F7%FB%E0%F3%B0%BE%B0%FF%E1%F5%C6%E0%EB%D3%F5%F3%FB%FC%B0%A8%B0%DC%F7%F1%F7%E1%FB%E6%F3%B2%F3%FE%B2%FF%F7%FC%FD%E1%B2%E7%FC%B2%B7%E1%B7%B2%F6%F7%B2%E0%F7%E1%E2%E7%F7%E1%E6%F3%E1%B2%F1%FD%E0%E0%F7%F1%E6%F3%E1%B2%E2%F3%E0%F3%B2%F1%FD%FC%E1%F7%F5%E7%FB%E0%B2%FE%F3%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%BC%B2%C4%E7%F7%FE%E4%F3%B2%F3%B2%FB%FC%E6%F7%FC%E6%F3%E0%FE%FD%BC%B0%BE%B0%FF%E1%F5%C4%FB%F6%F7%FD%DB%FC%E6%E0%FD%B0%A8%B0%C4%7F%F6%F7%FD%B2%F6%F7%B2%FB%FC%E6%E0%FD%F6%E7%F1%FBa%FC%B0%BE%B0%FF%E1%F5%D1%FE%FD%E1%F7%B0%A8%B0%D1%F7%E0%E0%F3%E0%B0%BE%B0%FF%E1%F5%DD%E2%E6%FB%FD%FC%B0%A8%B0%DD%E2%F1%FBa%FC%B0%BE%B0%FF%E1%F5%C0%FB%F1%F9%C6%F7%EA%E6%B0%A8%B0%C6%F7%EA%E6%FD%B2%F7%FC%E0%FB%E3%E7%F7%F1%FB%F6%FD%B0%BE%B0%FF%E1%F5%C7%E1%F7%D4%E7%FE%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%B0%A8%B0%F7%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B2%E3%E7%F7%B2%E1%F7%E0s%B2%FF%E7%EB%B2h%E6%FB%FE%B0%BE%B0%FF%E1%F5%DE%FD%F3%F6%FB%FC%F5%B0%A8%B0%D1%F3%E0%F5%F3%FC%F6%FD%BC%B2%D7%E1%E2%F7%E0%F7%B2%E2%FD%E0%B2%B2%F4%F3%E4%FD%E0%BC%BC%BC%B0%BE%B0%FF%E1%F5%DD%E0%F6%F7%E0%E1%B0%A8%B0%DD%E0%F6%F7%FC%F3%F6%F3%B2%E6%FD%F6%F3%E1%B2%FE%F3%E1%B2%E0%F7%E1%E2%E7%F7%E1%E6%F3%E1%B0%BE%B0%FF%E1%F5%DB%FC%F6%FB%F1%F3%E6%F7%C5%FD%E0%F6%B0%A8%B0%C2%E0%FD%E2%FD%E0%F1%FB%FD%FC%F7%B2%E7%FC%F3%B2%E2%F3%FE%F3%F0%E0%F3%B2%FD%B2%F7%EA%E2%E0%F7%E1%FBa%FC%B0%BE%B0%FF%E1%F5%DF%FD%E4%F7%DD%FC%F7%B0%A8%B0%C2%F3%E1%F3%E0%B0%BE%B0%FF%E1%F5%C2%FD%FB%FC%E6%E1%B0%A8%B0%E2%E7%FC%E6%FD%E1%B0%BE%B0%FF%E1%F5%D3%E7%F6%FB%FD%B0%A8%B0%D3%E7%F6%FB%FD%B0%BE%B0%FF%E1%F5%D1%FD%E0%E0%F7%F1%E6%B0%A8%B0%C1%F7%FE%F7%F1%F1%FBa%FC%B2%F1%FD%E0%E0%F7%F1%E6%F3%B0%BE%B0%FF%E1%F5%DB%FC%F1%FD%E0%E0%F7%F1%E6%B0%A8%B0%C1%F7%FE%F7%F1%F1%FBa%FC%B2%FB%FC%F1%FD%E0%E0%F7%F1%E6%F3%B0%BE%B0%FF%E1%F5%C7%FC%F1%FD%FF%E2%FE%F7%E6%F7%F6%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%F7%B2%FC%FD%FC%B2%F1%FD%FF%E2%FE%F7%E6%F3%F6%F3%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F4%E7%FE%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%F7%B2%E1%E7%E2%F7%E0%F3%F6%F3%BC%B2%C2%E7%FC%E6%E7%F3%F1%FBa%FC%A8%B2%B7%E1%B0%BE%B0%FF%E1%F5%C7%FC%E1%E7%F1%F1%F7%E1%E1%F4%E7%FE%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%F7%B2%FC%FD%FC%B2%E1%E7%E2%F7%E0%F3%F6%F3%BC%B2%C2%E7%FC%E6%E7%F3%F1%FBa%FC%A8%B2%B7%E1%B0%BE%B0%FF%E1%F5%C6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%C1%F7%FE%F7%F1%F1%FB%FD%FC%F3%B0%EF%EF
    01234

    Su navegador no es compatible con esta herramienta.

    Identifica y multiplica trozos de tartas para tu fiesta

    Multiplica la fracción de la izquierda por la de la derecha y escribe debajo su valor en forma a/b.

    %E9%B0%E6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%D1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FB%FC%E1%E6%E0%E7%F1%E6%FB%FD%FC%E1%B0%A8%B0%AE%E2%AC%DF%E7%FE%E6%FB%E2%FE%FB%F1%F3%B2%FE%F3%B2%F4%E0%F3%F1%F1%FBa%FC%B2%F6%F7%B2%FE%F3%B2%FB%E8%E3%E7%FB%F7%E0%F6%F3%B2%E2%FD%E0%B2%FE%F3%B2%F6%F7%B2%FE%F3%B2%F6%F7%E0%F7%F1%FA%F3%B2%EB%B2%F7%E1%F1%E0%FB%F0%F7%B2%F6%F7%F0%F3%F8%FD%B2%E1%E7%B2%E4%F3%FE%FD%E0%B2%F7%FC%B2%F4%FD%E0%FF%F3%B2%F3%BD%F0%BC%AE%BD%E2%AC%B0%BE%B0%E6%F7%EA%E6%C6%F7%EA%E6%B0%A8%B0%B7%A1%D1%E6%F3%F0%FE%F7%B7%A0%A2%F1%FE%F3%E1%E1%B7%A1%D6%B7%A0%A0%F7%EA%F7%BF%E6%F3%F0%FE%F7%B7%A0%A0%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A6%A7%A2%E2%EA%B7%A1%D0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%AA%A2%B7%A0%A7%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A1%D1%F1%F3%E2%E6%FB%FD%FC%B7%A1%D7%DF%E7%FE%E6%FB%E2%FE%FB%F1%F3%B7%A0%A2%F7%E1%E6%F3%E1%B7%A0%A2%F4%E0%F3%F1%F1%FB%FD%FC%F7%E1%B7%A0%A2%F7%B7%A0%A2%FB%FC%F6%FB%F1%F3%B7%A0%A2%F6%F7%F0%F3%F8%FD%B7%A0%A2%E1%E7%B7%A0%A2%F7%EA%E2%E0%F7%E1%FB%B7%D4%A1%FC%B7%A0%A2%F7%FC%B7%A0%A2%FE%F3%B7%A0%A2%F4%FD%E0%FF%F3%B7%A0%A2%F3%BD%F0%B7%A1%D1%BD%F1%F3%E2%E6%FB%FD%FC%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%FA%F7%F3%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%E0%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%FA%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A4%BC%AA%A2%A0%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A1%D1%BD%E6%FA%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%FA%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A1%A0%A3%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A1%D1%BD%E6%FA%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%FA%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A5%A5%A0%A4%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%C2%E0%FD%F6%E7%F1%E6%FD%B7%A1%D1%BD%E6%FA%B7%A1%D7%B7%A2%D3%B7%A1%D1%BD%E6%E0%B7%A1%D7%B7%A2%D3%B7%A1%D1%BD%E6%FA%F7%F3%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F0%FD%F6%EB%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%E0%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A3%A7%A7%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A3%A7%A7%E2%EA%B7%A1%D0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A4%BC%AA%A2%A0%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A1%D1%FB%FF%F5%B7%A0%A2%E1%E0%F1%B7%A1%D6%B7%A0%A0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%F4%A3%BC%E2%FC%F5%B7%A0%A0%B7%A0%A2%F3%FE%E6%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%A3%B7%A0%A0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%E6%FB%E6%FE%F7%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%A3%B7%A0%A2%B7%A0%AA%F1%C0%D7%D3%F5%F3%FE%B7%A0%AB%B7%A0%A0%B7%A0%A2%BD%B7%A1%D7%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A3%A7%A7%E2%EA%B7%A1%D0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A1%A0%A3%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A1%D1%FB%FF%F5%B7%A0%A2%E1%E0%F1%B7%A1%D6%B7%A0%A0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%F4%A5%BC%E2%FC%F5%B7%A0%A0%B7%A0%A2%F3%FE%E6%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%A5%B7%A0%A2%B7%A0%AA%F1%C0%D7%D3%F5%F3%FE%B7%A0%AB%B7%A0%A0%B7%A0%A2%E6%FB%E6%FE%F7%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%A3%B7%A0%A2%B7%A0%AA%F1%C0%D7%D3%F5%F3%FE%B7%A0%AB%B7%A0%A0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%BD%B7%A1%D7%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A5%A5%A0%A4%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%C2%FD%FC%B7%A0%A2%F7%FE%B7%A0%A2%E0%F7%E1%E7%FE%E6%F3%F6%FD%B7%A0%A2%E1%FB%FF%E2%FE%FB%F4%FB%F1%F3%F6%FD%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%BD%E6%E0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%E0%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A4%BC%AA%A2%A0%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%D2%D2%A3%BD%AA%D2%D2%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A1%A0%A3%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%D2%D2%A0%BD%A3%A2%D2%D2%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A5%A5%A0%A4%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%D2%D2%A3%BD%A6%A2%D2%D2%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%BD%E6%E0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%E0%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A4%BC%AA%A2%A0%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A1%D1%FB%FF%F5%B7%A0%A2%E1%E0%F1%B7%A1%D6%B7%A0%A0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%F4%A0%BC%E2%FC%F5%B7%A0%A0%B7%A0%A2%F3%FE%E6%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%A0%B7%A0%A2%B7%A0%AA%F1%C0%D7%D3%F5%F3%FE%B7%A0%AB%B7%A0%A0%B7%A0%A2%E6%FB%E6%FE%F7%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%A3%B7%A0%A2%B7%A0%AA%F1%C0%D7%D3%F5%F3%FE%B7%A0%AB%B7%A0%A0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%BD%B7%A1%D7%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A1%A0%A3%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A1%D1%FB%FF%F5%B7%A0%A2%E1%E0%F1%B7%A1%D6%B7%A0%A0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%F4%A7%BC%E2%FC%F5%B7%A0%A0%B7%A0%A2%F3%FE%E6%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%A7%B7%A0%A2%B7%A0%AA%F1%C0%D7%D3%F5%F3%FE%B7%A0%AB%B7%A0%A0%B7%A0%A2%E6%FB%E6%FE%F7%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%A7%B7%A0%A2%B7%A0%AA%F1%C0%D7%D3%F5%F3%FE%B7%A0%AB%B7%A0%A0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%BD%B7%A1%D7%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A5%A5%A0%A4%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%C2%FD%FC%B7%A0%A2%F7%FE%B7%A0%A2%E0%F7%E1%E7%FE%E6%F3%F6%FD%B7%A0%A2%E1%FB%FF%E2%FE%FB%F4%FB%F1%F3%F6%FD%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%BD%E6%E0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%E0%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A4%BC%AA%A2%A0%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%D2%D2%A5%BD%AA%D2%D2%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A1%A0%A3%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%D2%D2%A0%BD%A1%D2%D2%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A5%A5%A0%A4%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%D2%D2%A5%BD%A3%A0%D2%D2%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%BD%E6%E0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%E0%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A4%BC%AA%A2%A0%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A1%D1%FB%FF%F5%B7%A0%A2%E1%E0%F1%B7%A1%D6%B7%A0%A0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%F4%A1%BC%E2%FC%F5%B7%A0%A0%B7%A0%A2%F3%FE%E6%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%A1%B7%A0%A2%B7%A0%AA%F1%C0%D7%D3%F5%F3%FE%B7%A0%AB%B7%A0%A0%B7%A0%A2%E6%FB%E6%FE%F7%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%A1%B7%A0%A2%B7%A0%AA%F1%C0%D7%D3%F5%F3%FE%B7%A0%AB%B7%A0%A0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%BD%B7%A1%D7%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A1%A0%A3%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A1%D1%FB%FF%F5%B7%A0%A2%E1%E0%F1%B7%A1%D6%B7%A0%A0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%F4%AA%BC%E2%FC%F5%B7%A0%A0%B7%A0%A2%F3%FE%E6%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%AA%B7%A0%A2%B7%A0%AA%F1%C0%D7%D3%F5%F3%FE%B7%A0%AB%B7%A0%A0%B7%A0%A2%E6%FB%E6%FE%F7%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%AA%B7%A0%A2%B7%A0%AA%F1%C0%D7%D3%F5%F3%FE%B7%A0%AB%B7%A0%A0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%BD%B7%A1%D7%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A5%A5%A0%A4%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%C2%FD%FC%B7%A0%A2%F7%FE%B7%A0%A2%E0%F7%E1%E7%FE%E6%F3%F6%FD%B7%A0%A2%E1%FB%FF%E2%FE%FB%F4%FB%F1%F3%F6%FD%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%BD%E6%E0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%E0%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A4%BC%AA%A2%A0%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%D2%D2%A7%BD%AB%D2%D2%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A1%A0%A3%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%D2%D2%A7%BD%A3%A2%D2%D2%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A5%A5%A0%A4%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%D2%D2%A7%BD%A3%AA%D2%D2%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%BD%E6%E0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%E0%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A3%A7%A7%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A4%BC%AA%A2%A0%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A3%A7%A7%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A1%D1%FB%FF%F5%B7%A0%A2%E1%E0%F1%B7%A1%D6%B7%A0%A0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%F4%A6%BC%E2%FC%F5%B7%A0%A0%B7%A0%A2%F3%FE%E6%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%A6%B7%A0%A2%B7%A0%AA%F1%C0%D7%D3%F5%F3%FE%B7%A0%AB%B7%A0%A0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%E6%FB%E6%FE%F7%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%A6%B7%A0%A2%B7%A0%AA%F1%C0%D7%D3%F5%F3%FE%B7%A0%AB%B7%A0%A0%B7%A0%A2%BD%B7%A1%D7%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A1%A0%A3%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A3%A7%A7%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A1%D1%FB%FF%F5%B7%A0%A2%E1%E0%F1%B7%A1%D6%B7%A0%A0%E0%F7%E1%FD%E7%E0%F1%F7%E1%BD%F4%A4%BC%E2%FC%F5%B7%A0%A0%B7%A0%A2%F3%FE%E6%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%A6%B7%A0%A2%B7%A0%AA%F1%C0%D7%D3%F5%F3%FE%B7%A0%AB%B7%A0%A0%B7%A0%A2%E6%FB%E6%FE%F7%B7%A1%D6%B7%A0%A0%D4%E0%F3%F1%F1%FB%B7%D4%A1%FC%B7%A0%A2%A6%B7%A0%A2%B7%A0%AA%F1%C0%D7%D3%F5%F3%FE%B7%A0%AB%B7%A0%A0%B7%A0%A2%E5%FB%F6%E6%FA%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D6%B7%A0%A0%A3%A7%A2%B7%A0%A0%B7%A0%A2%BD%B7%A1%D7%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A5%A5%A0%A4%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%C2%FD%FC%B7%A0%A2%F7%FE%B7%A0%A2%E0%F7%E1%E7%FE%E6%F3%F6%FD%B7%A0%A2%E1%FB%FF%E2%FE%FB%F4%FB%F1%F3%F6%FD%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%BD%E6%E0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%E0%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A4%BC%AA%A2%A0%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%D2%D2%A1%BD%AB%D2%D2%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A1%A0%A3%AA%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A2%FA%F7%FB%F5%FA%E6%B7%A1%D3%B7%A0%A2%A0%A2%E2%EA%B7%A1%D0%B7%A0%A0%B7%A1%D7%D2%D2%A3%BD%A1%D2%D2%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%E6%F6%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E5%FB%F6%E6%FA%B7%A1%D3%B7%A0%A2%A1%A3%BC%A5%A5%A0%A4%B7%A0%A7%B7%A1%D0%B7%A0%A2%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%D2%D2%A3%BD%AB%D2%D2%B7%A1%D1%BD%E6%F6%B7%A1%D7%B7%A2%D3%B7%A1%D1%BD%E6%E0%B7%A1%D7%B7%A2%D3%B7%A1%D1%BD%E6%F0%FD%F6%EB%B7%A1%D7%B7%A2%D3%B7%A1%D1%BD%E6%F3%F0%FE%F7%B7%A1%D7%B7%A2%D3%B7%A1%D1%E2%B7%A0%A2%E1%E6%EB%FE%F7%B7%A1%D6%B7%A0%A0%E6%F7%EA%E6%BF%F3%FE%FB%F5%FC%B7%A1%D3%B7%A0%A2%F1%F7%FC%E6%F7%E0%B7%A1%D0%B7%A0%A0%B7%A1%D7%B7%D3%A3%D3%FC%B7%D7%D6%FF%F3%E6%F7%B7%A0%A2%F3%B7%A0%A2%FA%F3%F1%F7%E0%B7%A0%A2%E7%FC%F3%B7%A0%A2%E6%F3%E0%E6%F3%B7%A0%A2%F1%FD%FF%FD%B7%A0%A2%F7%E1%E6%F3%E1%B7%A0%A3%B7%A1%D1%BD%E2%B7%A1%D7%B0%BE%B0%E1%FA%FD%E5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%FB%E6%FB%FC%F7%E0%F3%E0%EB%B0%A8%E9%B0%E1%FA%FD%E5%D1%FE%E7%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FE%E7%F7%D5%F3%FF%F7%B0%A8%B0%B0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F5%F7%D1%FE%E7%F7%B0%A8%A6%A2%BE%B0%E1%FA%FD%E5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%BE%B0%FF%F7%E1%E1%F3%F5%F7%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%EF%BE%B0%F1%F3%E1%F7%C1%F7%FC%E1%FB%E6%FB%E4%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%FB%E1%C1%F1%FD%E0%FF%B0%A8%A3%BE%B0%E6%F7%EA%E6%D0%E7%E6%E6%FD%FC%C1%F1%FD%E0%FF%B0%A8%B0%D5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%E0%F7%E2%F7%F3%E6%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%E6%E0%E7%F7%BE%B0%E6%F7%EA%E6%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%B0%BE%B0%E6%F7%EA%E6%D3%F4%E6%F7%E0%B0%A8%B0%B0%BE%B0%F4%F7%F7%F6%D0%F3%F1%F9%B0%A8%F4%F3%FE%E1%F7%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F8%F7%D4%D0%B0%A8%A3%A2%A2%BE%B0%E4%F7%E0%E1%FB%FD%FC%B0%A8%A3%BE%B0%F7%E1%E6%E0%FB%F1%E6%D1%FA%F7%F1%F9%B0%A8%F4%F3%FE%E1%F7%BE%B0%E5%FD%E0%F6%E1%C1%FB%E8%F7%B0%A8%E6%E0%E7%F7%BE%B0%E6%FB%FF%F7%B0%A8%A2%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%E5%FD%E0%F6%E1%D7%E0%E0%FD%E0%E1%B0%A8%B0%B0%BE%B0%F3%E6%E6%F7%FF%E2%E1%DC%E7%FF%F0%F7%E0%B0%A8%A0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F8%F7%D7%E0%E0%FD%E0%B0%A8%A0%A2%BE%B0%E1%FA%FD%E5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%F4%F3%FE%E1%F7%BE%B0%E5%FD%E0%F6%E1%DE%FB%FF%FB%E6%B0%A8%F4%F3%FE%E1%F7%BE%B0%F7%E4%F3%FE%E7%F3%E6%FB%FD%FC%B0%A8%F4%F3%FE%E1%F7%BE%B0%F7%E4%F3%FE%E7%F3%E6%FB%FD%FC%DB%D6%B0%A8%B0%B0%BE%B0%FB%F6%B0%A8%B0%A0%A2%A0%A7%A3%A2%A0%A7%A3%A7%A3%A0%A0%A0%BF%A3%A0%A2%B0%BE%B0%FF%E1%F5%E1%B0%A8%E9%B0%FF%E1%F5%DA%F3%E2%E2%F7%FC%B0%A8%B0%C2%F3%E1%F3%E0%B0%BE%B0%FF%E1%F5%C0%F7%E2%FE%EB%B0%A8%B0%C0%F7%E1%E2%FD%FC%F6%F7%E0%B0%BE%B0%FF%E1%F5%C1%E7%F0%FF%FB%E6%B0%A8%B0%D7%FC%E4%FB%F3%E0%B0%BE%B0%FF%E1%F5%D7%FC%E6%F7%E0%D1%FD%F6%F7%B0%A8%B0%DB%FC%E6%E0%FD%F6%E7%E8%F1%F3%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%D1%FD%F6%F7%B0%A8%B0%D7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B2%FC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B0%BE%B0%FF%E1%F5%D5%F3%FF%F7%DD%E4%F7%E0%B0%A8%B03%D4%FB%FC%B2%F6%F7%B2%FE%F3%B2%E2%F3%E0%E6%FB%F6%F3%B3%B0%BE%B0%FF%E1%F5%DB%FC%F6%FB%F1%F3%E6%F7%C5%FD%E0%F6%B0%A8%B0%C2%E0%FD%E2%FD%E0%F1%FB%FD%FC%F7%B2%E7%FC%F3%B2%E2%F3%FE%F3%F0%E0%F3%B2%FD%B2%F7%EA%E2%E0%F7%E1%FBa%FC%B0%BE%B0%FF%E1%F5%D1%FE%E7%F7%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B2%DE%F3%B2%E2%FB%E1%E6%F3%B2%F7%E1%A8%B0%BE%B0%FF%E1%F5%CB%FD%E7%DA%F3%E1%B0%A8%B0%C6%FB%F7%FC%F7%B2%B7%A3%B2%F3%F1%FB%F7%E0%E6%FD%E1%B2%EB%B2%B7%A0%B2%F4%F3%FE%FE%FD%E1%B0%BE%B0%FF%E1%F5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%D1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%D3%F5%F3%FB%FC%B0%A8%B0%D8%E7%F5%F3%E0%B2%FD%E6%E0%F3%B2%E4%F7%E8%B0%BE%B0%FF%E1%F5%C0%F7%E3%E7%FB%E0%F7%F6%D3%F1%F1%F7%E1%E1%D9%F7%EB%B0%A8%B0%D7%E1%B2%FC%F7%F1%F7%E1%F3%E0%FB%FD%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%DE%FD%FD%F9%FB%FC%F5%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B2%DE%F3%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B2%E3%E7%F7%B2%F7%E1%E6%F3%F0%F3%B2%F0%E7%E1%F1%F3%FC%F6%FD%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%E6%F3%E0%E6%B0%A8%B0%C2%E7%FE%E1%F7%B2%F3%E3%E7%7F%B2%E2%F3%E0%F3%B2%F8%E7%F5%F3%E0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%E1%B0%A8%B0%D7%E0%E0%FD%E0%F7%E1%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%B0%A8%B0%D7%E0%E0%FD%E0%B0%BE%B0%FF%E1%F5%DF%FD%E4%F7%DD%FC%F7%B0%A8%B0%C2%F3%E1%F3%E0%B0%BE%B0%FF%E1%F5%DA%FB%E6%E1%B0%A8%B0%D3%F1%FB%F7%E0%E6%FD%E1%B0%BE%B0%FF%E1%F5%DA%FB%E6%B0%A8%B0%D3%F1%FB%F7%E0%E6%FD%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%B0%DF%FB%FC%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%DF%F3%EA%FB%FF%FB%E8%F7%B0%A8%B0%DF%F3%EA%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%C6%FB%FF%F7%B0%A8%B0%DE%7F%FF%FB%E6%F7%B2%F6%F7%B2%E6%FB%F7%FF%E2%FD%B2%BA%FF%FF%A8%E1%E1%BB%B0%BE%B0%FF%E1%F5%DE%FB%E4%F7%B0%A8%B0%C4%FB%F6%F3%B0%BE%B0%FF%E1%F5%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C2%F3%FC%E6%F3%FE%FE%F3%B2%D1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%D7%EA%FB%E6%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C1%F3%FE%FB%E0%B2%F6%F7%FE%B2%FF%FD%F6%FD%B2%E2%F3%FC%E6%F3%FE%FE%F3%B2%F1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%DC%E7%FF%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%B0%DCh%FF%F7%E0%FD%B2%F6%F7%B2%E2%E0%F7%F5%E7%FC%E6%F3%E1%B0%BE%B0%FF%E1%F5%DC%FD%DB%FF%F3%F5%F7%B0%A8%B0%C2%E0%F7%F5%E7%FC%E6%F3%B2%E1%FB%FC%B2%FB%FFs%F5%F7%FC%F7%E1%B0%BE%B0%FF%E1%F5%D1%FD%FD%FE%B0%A8%B03%D0%FB%F7%FC%B3%B0%BE%B0%FF%E1%F5%DE%FD%E1%F7%C6%B0%A8%B0%DA%F3%B2%E2%F7%E0%F6%FB%F6%FD%B2%A1%A1%A2%B2%E2%E7%FC%E6%FD%E1%B0%BE%B0%FF%E1%F5%DE%FD%E1%F7%DE%FB%E4%F7%B0%A8%B0%DA%F3%B2%E2%F7%E0%F6%FB%F6%FD%B2%E7%FC%F3%B2%E4%FB%F6%F3%B0%BE%B0%FF%E1%F5%DE%FD%E1%E6%DE%FB%E4%F7%E1%B0%A8%B03%DA%F3%B2%E2%F7%E0%F6%FB%F6%FD%B2%E6%FD%F6%F3%E1%B2%E1%E7%E1%B2%E4%FB%F6%F3%E1%B3%B0%BE%B0%FF%F5%E1%D3%FE%FE%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%B03%D1%FD%FF%E2%FE%F7%E6%F3%F6%F3%E1%B2%FE%F3%E1%B2%E2%E0%F7%F5%E7%FC%E6%F3%E1%B3%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F7%E1%B0%A8%B03%D1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%D7%EA%F1%F7%FE%F7%FC%E6%F7%B3%B2%EE%B23%D5%F7%FC%FB%F3%FE%B3%B2%EE%B23%DF%E7%EB%B2%F0%FB%F7%FC%B3%B2%EE%B23%C2%F7%E0%F4%F7%F1%E6%FD%B3%B0%BE%B0%FF%E1%F5%D4%F3%FB%FE%E7%E0%F7%E1%B0%A8%B03%DC%FD%B2%F7%E0%F3%B2%F7%E1%FD%B3%B2%EE%B23%DB%FC%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DE%FD%B2%E1%F7%FC%E6%FB%FF%FD%E1%B3%B2%EE%B23%D7%E0%E0%FD%E0%B3%B0%BE%B0%FF%E1%F5%C6%E0%EB%D3%F5%F3%FB%FC%B0%A8%B0%DC%F7%F1%F7%E1%FB%E6%F3%B2%F3%FE%B2%FF%F7%FC%FD%E1%B2%E7%FC%B2%B7%E1%B7%B2%F6%F7%B2%E0%F7%E1%E2%E7%F7%E1%E6%F3%E1%B2%F1%FD%E0%E0%F7%F1%E6%F3%E1%B2%E2%F3%E0%F3%B2%F1%FD%FC%E1%F7%F5%E7%FB%E0%B2%FE%F3%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%BC%B2%C4%E7%F7%FE%E4%F3%B2%F3%B2%FB%FC%E6%F7%FC%E6%F3%E0%FE%FD%BC%B0%BE%B0%FF%E1%F5%C5%E0%FD%E6%F7%B0%A8%B0%D7%E1%F1%E0%FB%F0%F3%B2%FE%F3%B2%E2%F3%FE%F3%F0%E0%F3%B2%F1%FD%E0%E0%F7%F1%E6%F3%B2%EB%B2%E2%E7%FE%E1%F7%B2%F7%FC%B2%C0%F7%E1%E2%FD%FC%F6%F7%E0%BC%B2%C1%FB%B2%F6%E7%F6%F3%BE%B2%E2%E7%FE%E1%F7%B2%F7%FC%B2%C1%F7%F5%E7%FB%E0%BC%B0%BE%B0%FF%E1%F5%DC%FD%E6%DC%F7%E6%E5%FD%E0%F9%B0%A8%B0%D3%B2%F7%E1%E6%F7%B2%F8%E7%F7%F5%FD%B2%E1a%FE%FD%B2%E1%F7%B2%E2%E7%F7%F6%F7%B2%F8%E7%F5%F3%E0%B2%F1%FD%FC%B2%F1%FD%FC%F7%EA%FBa%FC%B2%F3%B2%FB%FC%E6%F7%E0%FC%F7%E6%BC%B0%BE%B0%FF%E1%F5%D7%FC%F6%D5%F3%FF%F7%C1%F1%FD%E0%F7%B0%A8%B0%D3%FC%E6%F7%E1%B2%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F1%FD%FF%FB%F7%FC%F1%F7%B2%FE%F3%B2%E2%F3%E0%E6%FB%F6%F3%BC%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%C1%F1%FD%E0%FF%B0%A8%B0%DE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%FC%FD%B2%E1%F7%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%E2%FD%E0%E3%E7%F7%B2%F7%E1%E6%F3%B2%E2s%F5%FB%FC%F3%B2%FC%FD%B2%F4%FD%E0%FF%F3%B2%E2%F3%E0%E6%F7%B2%B2%F6%F7%B2%E7%FC%B2%E2%F3%E3%E7%F7%E6%F7%B2%C1%D1%DD%C0%DF%BC%B0%BE%B0%FF%E1%F5%C3%E7%F7%E1%E6%FB%FD%FC%B0%A8%B0%C2%E0%F7%F5%E7%FC%E6%F3%B0%BE%B0%FF%E1%F5%D3%FC%E1%E5%F7%E0%B0%A8%B0%C0%F7%E1%E2%FD%FC%F6%F7%E0%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%C1%F1%FD%E0%F7%B0%A8%B03%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E7%FC%F3%B2%E4%F7%E8%B3%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%B0%A8%B0%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%B0%BE%B0%FF%E1%F5%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%B0%A8%B0%DB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%CB%FD%E7%C1%F1%FD%E0%F7%B0%A8%B0%C1%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%D3%E7%E6%FA%FD%E0%B0%A8%B0%D3%E7%E6%FD%E0%7F%F3%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C1%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%BC%B2%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F8%E7%F5%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%BC%B0%BE%B0%FF%E1%F5%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C1%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F3%E7%E6%FD%FFs%E6%FB%F1%F3%FF%F7%FC%E6%F7%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%BC%B0%BE%B0%FF%E1%F5%C1%F7%E4%F7%E0%F3%FE%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E6%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%F1%FD%FF%FD%B2%E3%E7%FB%F7%E0%F3%B0%BE%B0%FF%E1%F5%CB%FD%E7%DE%F3%E1%E6%C1%F1%FD%E0%F7%B0%A8%B0%DE%F3%B2h%FE%E6%FB%FF%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F5%E7%F3%E0%F6%F3%F6%F3%B2%F7%E1%B0%BE%B0%FF%E1%F5%D3%F1%E6%FB%E6%EB%D1%FD%FF%E2%FE%EB%B0%A8%B0%CB%F3%B2%FA%F3%B2%E0%F7%F3%FE%FB%E8%F3%F6%FD%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%BC%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%F7%E4%F7%E0%F3%FE%C6%FB%FF%F7%E1%B0%A8%B0%C2%E7%F7%F6%F7%B2%E0%F7%F3%FE%FB%E8%F3%E0%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%B2%F1%E7%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%E3%E7%FB%F7%E0%F3%B0%BE%B0%FF%E1%F5%D1%FE%FD%E1%F7%B0%A8%B0%D1%F7%E0%E0%F3%E0%B0%BE%B0%FF%E1%F5%DE%FD%F3%F6%FB%FC%F5%B0%A8%B0%D1%F3%E0%F5%F3%FC%F6%FD%BC%B2%D7%E1%E2%F7%E0%F7%BE%B2%E2%FD%E0%B2%F4%F3%E4%FD%E0%BC%BC%BC%B0%BE%B0%FF%E1%F5%C2%FD%FB%FC%E6%E1%B0%A8%B0%E2%E7%FC%E6%FD%E1%B0%BE%B0%FF%E1%F5%D3%E7%F6%FB%FD%B0%A8%B0%D3%E7%F6%FB%FD%B0%BE%B0%FF%E1%F5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%B0%C1%FD%FE%E7%F1%FBa%FC%B0%BE%B0%FF%E1%F5%C6%E0%EB%B0%A8%B03%C2%E0%E7%F7%F0%F3%B2%FD%E6%E0%F3%B2%E4%F7%E8%B3%B0%BE%B0%FF%E1%F5%D1%FA%F7%F1%F9%B0%A8%B0%D1%FD%FF%E2%E0%FD%F0%F3%E0%B0%BE%B0%FF%E1%F5%D7%FC%F6%C1%F1%FD%E0%F7%B0%A8%B0%DA%F3%E1%B2%E6%F7%FC%FB%F6%FD%B2%B7%E1%B2%F3%F1%FB%F7%E0%E6%FD%E1%B2%EB%B2%B7%F6%B2%F7%E0%E0%FD%E0%F7%E1%BC%B0%BE%B0%FF%E1%F5%D7%FC%F6%C6%FB%FF%F7%B0%A8%B0%D7%FE%B2%E6%FB%F7%FF%E2%FD%B2%FA%F3%B2%F4%FB%FC%F3%FE%FB%E8%F3%F6%FD%BC%B0%BE%B0%FF%E1%F5%D5%F3%FF%F7%D7%FC%F6%B0%A8%B0%DA%F3%E1%B2%F1%FD%FF%E2%FE%F7%E6%F3%F6%FD%B2%FE%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%B0%BE%B0%FF%E1%F5%C7%FC%F1%FD%FF%E2%FE%F7%E6%F7%F6%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%FC%FD%B2%F1%FD%FF%E2%FE%F7%E6%F3%F6%F3%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F4%E7%FE%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%E1%E7%E2%F7%E0%F3%F6%F3%BC%B2%C2%E7%FC%E6%E7%F3%F1%FBa%FC%A8%B2%B7%E1%B0%BE%B0%FF%E1%F5%C7%FC%E1%E7%F1%F1%F7%E1%E1%F4%E7%FE%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%FC%FD%B2%E1%E7%E2%F7%E0%F3%F6%F3%BC%B2%C2%E7%FC%E6%E7%F3%F1%FBa%FC%A8%B2%B7%E1%B0%BE%B0%FF%E1%F5%C6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%D1%FD%FF%E2%FE%F7%E6%F3%B0%EF%EF
    Multiplica estas fracciones e indica debajo su expresión en la forma a/b
    Fracción Fracción Producto
    Fracción 1 Fracción 7 (cREAgal) Pon el resultado simplificado
    @@1/8@@ @@2/10@@ @@1/40@@
    Fracción 2 (cREAgal) Fracción 5 (cREAgal) Pon el resultado simplificado
    @@7/8@@ @@2/3@@ @@7/12@@
    Fracción 3 (cREAgal) Fracción 8 (cREAgal) Pon el resultado simplificado
    @@5/9@@ @@5/10@@ @@5/18@@
    Fracción 4 (cREAgal) Fracción 4 (cREAgal) Pon el resultado simplificado
    @@3/9@@ @@1/3@@ @@1/9@@

    ¡Anímate a hacer una tarta como estas!

    Su navegador no es compatible con esta herramienta.

    Creado con eXeLearning (Ventana nueva)