Misma pizza, trozos diferentes
Para la fiesta encargas tres pizzas.
Son de lacón con grelos.
¡Tu favorita!
Pero, ¿Cómo la repartes?
¿Cuánto se comió?
Las tres pizzas las decides cortar del siguiente modo:
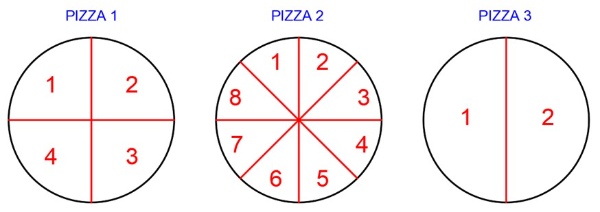
Si de la primera se comen 2 trozos se comen \(\frac{2}{4}\) de la pizza.
Si de la segunda se comen 4 trozos se comen \(\frac{4}{8}\) de la pizza.
Si de la tercera se come 1 trozo se come \(\frac{1}{2}\) de la pizza.
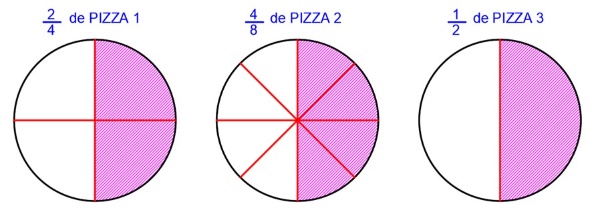
Pero, se ha comido lo mismo. ¿No?
Fracciones equivalentes
¡Efectivamente! Se han comido las mismas cantidades en cada pizza.
No importa si cortas la pizza en 2, 4 u 8 trozos.
Si te comes la mitad, siempre te has comido la misma cantidad.
Por eso, las fracciones \(\frac{1}{2}\), \(\frac{2}{4}\) y \(\frac{4}{8}\) son equivalentes.
Se escriben con números diferentes, pero representan la misma cantidad.
¿Cómo sabes que son equivalentes?
Para saber si dos fracciones son equivalentes, puedes multiplicar sus términos en cruz.
Si el resultado obtenido es el mismo, las fracciones son equivalentes.
\(\Large\frac{1}{2}=\frac{3}{6}\Rightarrow\)\(1\times6=2\times3\Rightarrow\)\(6=6\)
¿Cómo las obtienes?
Si quieres conseguir una fracción equivalente a otra, multiplicas numerador y denominador por el mismo número.
Por ejemplo, la fracción \(\Large\frac{1}{2}\) y quiero obtener fracciones equivalentes a ella:
\(\Large\frac{1}{2}=\frac{1\times2}{2\times2}=\frac{2}{4}=\frac{2\times7}{4\times7}=\frac{14}{28}=\dotsc\)