Eligiendo la tarta
 Para poder elegir la mejor tarta para la fiesta, decides ir al mercado a comprar para probarla.
Para poder elegir la mejor tarta para la fiesta, decides ir al mercado a comprar para probarla.
En la pastelería, te explican los diferentes tamaños disponibles.
En la sección de tartas grandes, tienen una tarta dividida en 10 porciones iguales.
Compras la tarta entera, pero el domingo tu familia y tú os coméis 7 porciones.
¿Qué fracción de la tarta se ha comido tu familia? ¿Y qué fracción de la tarta queda para el resto de la semana.
Solución
El domingo compraste la tarta entera dividida en 10 partes.
Y tú y tu familia, comisteis ese día 7 porciones, es decir \(\frac{7}{10}\) de la tarta.
Para saber lo que falta, piensa:
- La unidad completa es \(\frac{10}{10}\), pero ya comisteis \(\frac{7}{10}\) de la tarta.
- Restas los numeradores \(\frac{10-7}{10}\) y obtienes lo que falta por comer \(\frac{3}{10}\) de la tarta.
Explicación
¿Sabes que hay fracciones que son iguales a la unidad, o que valen la unidad?
Pues sí, son fracciones como éstas:
\(\frac{2}{2}\) = \(\frac{5}{5}\) = \(\frac{9}{9}\) = \(\frac{12}{12} = 1\)
Estas fracciones tienen el mismo numerador y denominador, entonces representan la unidad.
Ejemplos
Si te fijas, puedes ver que se eligen la misma cantidad de partes que tiene la unidad al completo.
Por ejemplo, si partes una naranja en dos y te comes las dos partes, entonces habrás comido dos de dos, \(\frac{2}{2}\), que es lo mismo que una naranja entera.
Si divides el numerador entre el denominador de estas fracciones, el resultado es uno.
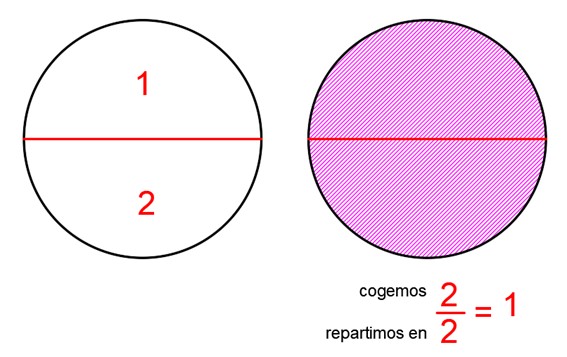
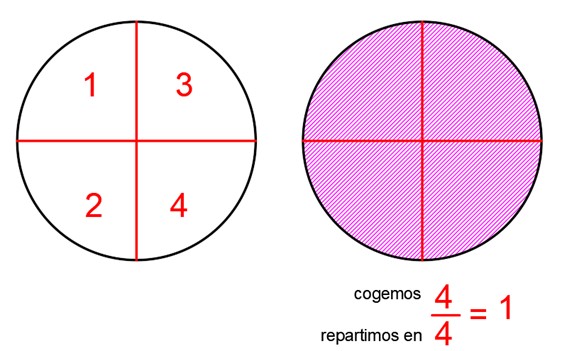
Unidad al completo
El domingo compraste tarta entera que dividiste en 10 partes.
Y tú y tu familia, comisteis ese día 7 porciones, es decir \(\frac{3}{10}\) de la tarta.
¿Cuántas porciones faltan por comer? ¿Cómo lo calculamos?
Para saber lo que falta, solo tienes que pensar en la fracción que tienes y restársela a la unidad completa.
- La unidad completa es \(\frac{10}{10}\), pero ya comisteis \(\frac{3}{10}\) de la tarta.
- Restas los numeradores y obtienes lo que falta por comer \(\frac{7}{10}\) de la tarta.
