2.4. El radián
Definición de radián
En la vida cotidiana estamos acostumbrados a medir ángulos en grados, minutos y segundos. Nos son familiares los ángulos sexagesimales para los cuales el ángulo completo mide 360º.
Sin embargo, los matemáticos prefieren medir los ángulos en otra unidad llamada radián.
Un radián es la amplitud de un ángulo central de una circunferencia que abarca un arco de la misma longitud que el radio.

Actividad 1
¿Cuántos grados mide un radián? ¿Es independiente del radio de la circunferencia?
Utilizaremos el siguiente applet para contestar a estas preguntas.
Mueve el punto P de la primera circunferencia hasta que logres tener un arco con la misma longitud que el radio. ¿Cuántos grados mide el ángulo?
Ahora, haz lo mismo con el punto Q de la otra circunferencia. ¿Cuántos grados mide el ángulo? ¿Sucederá siempre lo mismo?
Mueve el deslizador para hacer variar el radio de la segunda circuferencia.
Conclusión:
Sí, el radián es independiente del radio por lo que sirve como unidad para medir ángulos.
Parece que 1 rad viene siendo un ángulo de entre 57,1º y 57,4º, pero intentaremos dar una equivalencia exacta.
Acitvidad 2
¿Cuántos radianes caben en una circunferencia?
Marca la casilla Múltiplos del radián.
Mueve el deslizador para ver los ángulos, 1 rad, 2 rad, 3 rad... ¿Puedes decir de forma aproximada cuántos radianes caben en la circunferencia?
Marca la casilla Múltiplos de π·rad.
Mueve el deslizador para ver π rad, 2π rad, 3π rad... ¿Puedes decir de forma exacta cuántos radianes caben en la circunferencia?
Equivalencia entre grados y radianes
Con lo que ya sabíamos sobre ángulos y arcos era suficiente para saber cuántos radianes contiene el ángulo completo.
Basta con dividir la longitud de la circunferencia (2πR) entre el arco correspondiente a un radián, R: ![]()
Por proporcionalidad el ángulo completo contiene tantos radianes como radios contiene la longitud de la circunferencia.
Es decir, en una circunferencia caben 2π radianes, o lo que es lo mismo, el ángulo completo mide 2π radianes.
Ya tenemos la equivalencia exacta entre grados y radianes: ![]()
Factores de conversión:
Podemos escribir los factores de conversión: ![]() y
y ![]()
El primero sirve para pasar de grados a radianes y el segundo, de radianes a grados.
Sólo hay que tener en cuenta que si multiplicamos una cantidad por 1, la cantidad no varía. Y que además, las unidades se pueden simplificar en una fracción de la misma forma que se hace con los factores que se repiten en numerador y denominador.
Ejemplos de uso:
![]()
![]()
Nota:
También es frecuente trabajar con los factores de conversión simplificados. Esto es:
![]() y
y ![]()
Actividad 3
Relación de la longitud de arco y el ángulo central.
Ya sabíamos que existe una relación entre un ángulo central de una circunferencia y el arco que abarca. Sabemos que la amplitud del ángulo central y la del arco son directamente proporcionales. Todo esto se puede comprobar en el siguiente applet.
Utiliza el deslizador para obtener un ángulo de 30º y fíjate en la longitud del arco que subtiende.
Ahora, haz que la amplitud del ángulo sea el doble y observa si sucede lo mismo con el arco.
Haz que sea el triple y el cuádruple y comprueba el arco.
La relación entre el arco y el ángulo en una circunferencia viene dada por al expresión:
![]() de donde
de donde ![]() donde α es el ángulo central medido en grados y L, la longitud del arco.
donde α es el ángulo central medido en grados y L, la longitud del arco.
Teniendo en cuenta la equivalencia entre el radián y el grado, podemos escribir ![]() donde α es el ángulo medido en radianes.
donde α es el ángulo medido en radianes.
Esta expresión es mucho más sencilla que la anterior y todas las fórmulas que de ella se puedan derivar, que no son pocas, heredarán su simplicidad.
Ángulos notables de la circunferencia en radianes
Utilizando la equivalencia entre grados y radianes podemos escribir los ángulos de 30º, 45º, 90º... en radianes.
Es conveniente aprenderse de memoria su medida en radianes.
Actividad 4
Introduce en la casilla de entrada del applet el valor de los ángulos de 30º, 45º, 60º, 90º, 120º, 135º, 150º, 180º
Si divides la circunferencia en dos partes iguales, ¿cuántos radianes mide cada sector?
Si divides la circunferencia en 4 partes iguales, ¿cuántos radianes mide cada sector?
Si divides la circunferencia en 6 partes iguales, ¿cuánto mide cada sector?
En la siguiente imagen se muestran los ángulos más notables escritos en radianes.
A partir de estos puedes conocer todos sus múltiplos.
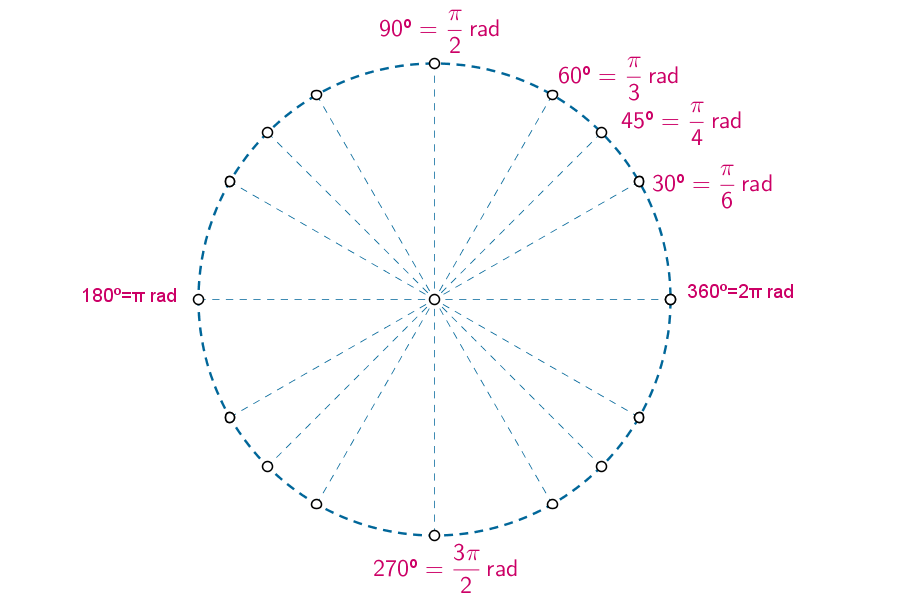
Equivalencia entre ángulos y radianes:
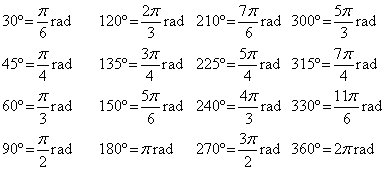
Actividad 5
Expresa en radianes los siguientes águlos
Actividad 6
Expresa en grados los siguientes ángulos:
Actividad 7
Indica a qué cuadrante pertenecen los siguientes ángulos
Actividad 8
Sabiendo que α es un ángulo del primer cuadrante: