El agua que une: de Verín a Vidago
El agua ha modelado el paisaje y la vida de las tierras que se extienden a ambos lados del río Támega. Desde Verín, en Galicia, hasta Vidago, en Portugal, el agua fluye como un elemento común, presente en manantiales, fuentes termales y balnearios.
En esta nueva propuesta, te adentrarás en el balneario de Vidago, deteniéndote en el pabellón en el que se encuentra la fuente termal. La vidriera circular de este pabellón, visible desde el interior del edificio, será tu punto de partida para explorar diversas figuras geométricas vinculadas con la circunferencia: sectores, posiciones relativas entre circunferencias y más.
Lectura facilitada
El agua ha dado forma al paisaje y a la vida en las tierras cercanas al río Támega.
Desde Verín hasta Vidago, el agua está presente en manantiales, fuentes termales y balnearios.
Ahora vas a conocer el balneario de Vidago.
En este balneario hay un pabellón que tiene una fuente termal.
En este pabellón también hay una vidriera redonda que se puede ver desde dentro.
Vas a usar esta vidriera para aprender sobre figuras geométricas relacionadas con círculos y circunferencias, tales como sectores y posiciones entre circunferencias.
Arco: parte de la circunferencia comprendida entre dos puntos de esta.
Cuerda: segmento que une dos puntos de la circunferencia.
Segmento circular: parte del círculo limitada por una cuerda y el arco correspondiente.
Sector circular: parte del círculo limitada por dos radios y el arco que los une.
Corona circular: zona comprendida entre dos circunferencias concéntricas (con el mismo centro) de distinto radio.
Trapecio circular: porción de círculo limitada por dos radios y una corona circular.
Circunferencias concéntricas: circunferencias con el mismo centro y diferentes radios.
Circunferencias interiores: la distancia entre los dos centros es menor que la diferencia de los radios.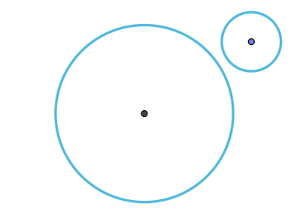
Circunferencias exteriores: la distancia entre los dos centros es mayor que la suma de los radios.
Circunferencias secantes: circunferencias que tienen dos puntos en común.
Circunferencias tangentes interiores: circunferencias que tienen un punto en común y cuya distancia entre los dos centros es igual a la resta de los radios.
Circunferencias tangentes exteriores: circunferencias que tienen un punto en común y cuya distancia entre los dos centros es igual a la suma de los radios.
