El balneario de Mondariz
El Balneario de Mondariz, inaugurado a finales del siglo XIX, ha sido refugio de turistas atraídos por su manantial de aguas termales.
Hoy, sus elegantes jardines son el escenario perfecto para descubrir las formas circulares presentes en fuentes, piscinas y parterres.
Así, compás y regla en mano, medirás radios y calcularás áreas mientras exploras, con ojos matemáticos, la armonía de sus espacios curvos.
Lectura facilitada
El Balneario de Mondariz abrió a finales del siglo XIX.
Desde entonces, muchas personas lo han visitado por su manantial de aguas termales.
Hoy sus jardines son un lugar perfecto para observar formas redondas.
Con compás y regla, vas a medir radios y calcular áreas.
Así descubrirás, con ojos matemáticos, la belleza de sus formas circulares.
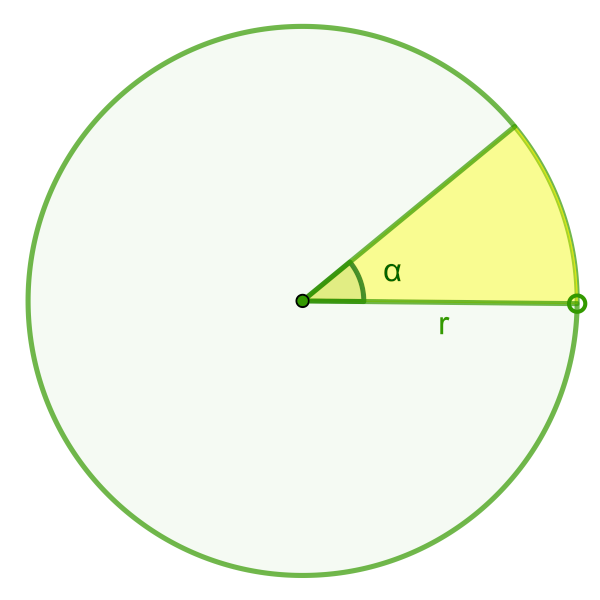
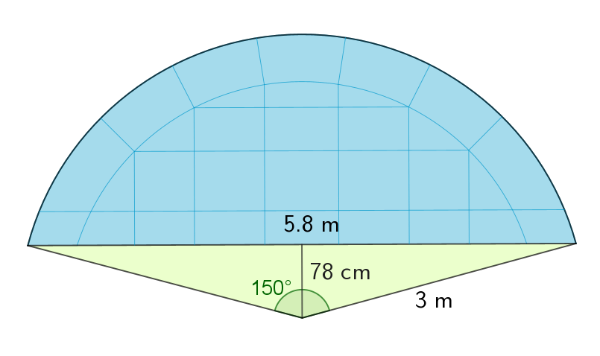
En el suelo del pabellón de la fuente, en el Balneario de Mondariz, hay una zona especialmente deteriorada por el agua que cae directamente desde la fuente. Esa zona tiene forma de segmento circular.
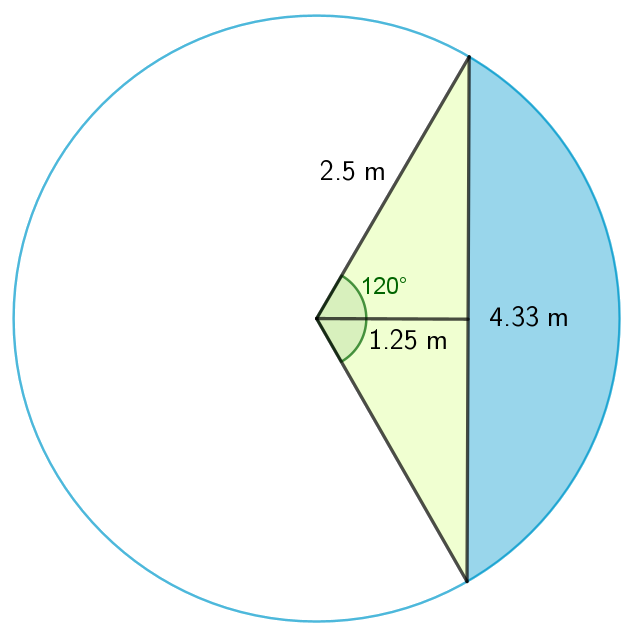
Después de todo lo trabajado hasta ahora y antes de completar esta fase, reflexiona en tu