Skip navigation

8. Series circuits

Series circuits

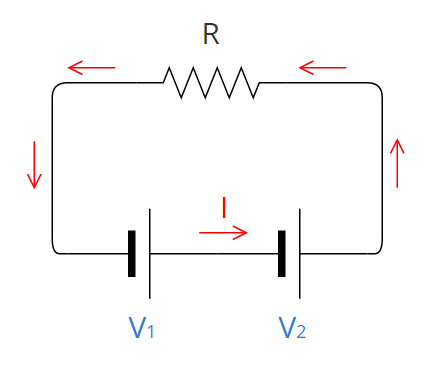
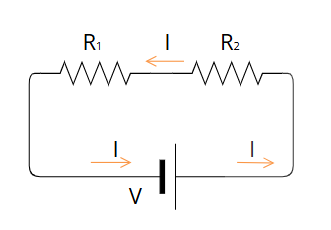
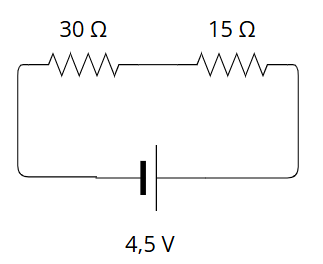
The word series means: "Set of things that follow one another." A series circuit is one where the elements are placed one after the other. The negative pole of each element (from which the electrons come out) is connected to the positive pole of the next one (through which the electrons enter).

In a series circuit, electrons pass in equal number and at the same speed through all the elements. The intensity in a series circuit is the same at all its points.


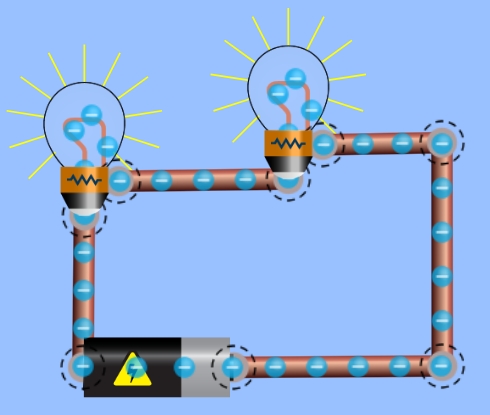
Simución de PhET Interactive Simulations, University of Colorado Boulder. https://phet.colorado.edu. CC-BY-4.0 
 

Batteries in series

When two batteries are connected in series, the electrons pass first through one, gaining the energy given by that battery, and then through the other one, gaining the energy given by it. The energy they gain in total is the addition of both:

V = V 1 +V 2

The current is the same in all points and can be calculated applying Ohm´s Law:

Notice how, in the figure, the positive terminal of one battery (the long line of the battery symbol) is connected to the negative terminal of the other (the short line), as corresponds to the series connection.

Audio::

Example. Fill in the gaps

Read and fill in the blanks.

A series circuit consists of two 12 V batteries and a motor, through which a current of 4 A is flowing. Calculate the resistance of the motor.

The total voltage to which the motor is connected is the sum of the voltages of the two batteries, when connected in series: V = V 1 + V 2 = + = 24

According to Ohm's law: R = V / I = / = 6 Ω

Audio: 

Enable JavaScript

Resistors in series

In a circuit with resistors connected in series, the electrons pass through all of them, one after the other. The total resistance of the circuit will be the adition of the resistances of all the elements:

R = R1 + R2

The current that passes through the circuit is calculated taking this and Ohm's law into account:



It will not be lost the same energy in all resistors unless they are equal. If one resistor is larger than the other, more energy will be lost in that one. 

The energy per unit charge lost in each of them (potential difference) will be, according to Ohm's law:

At resistor 1:         V1  = I · R1

At resistor 2:       V2  = I · R2 

V1 and V2 are the potential differences between both ends of each resistor (figure). Since the total energy that the electrons carry when they leave the battery (V) must be used to cross the two resistors: 

V = V1  + V2

Audio: 

Step by step exercise. Fill in the gaps

Calculate the equivalent resistance and the current intensity that flows through the circuit in the figure. Fill in the blanks.

Known quantities:  R1 = 30 Ω,  R2 =   Ω,  V = 4.5 V

Unknown quantities : R, I

Formulas:

Total or equivalent resistance of the series circuit:  R = R1 + R2

Ohm´s Law:  V = · R

We want to calculate I, so we rearrange Ohm´s Law to become: 

I =

Plug in the values:

R = 30 + 15 = 45 Ω

I = V / R =  / = 0.1

Audio: 

Enable JavaScript

Exercise. Fill in the gaps

Two resistors are connected in series to a 9 V battery, one of  0.04 kΩ and the other of 60 Ω .

a) Calculate the voltage across the 0.04 kΩ resistor and the current that flows through the circuit.

b) What energy per unit of charge is lost in the other resistance?

Fill in the blanks.

Known quantities:  R1 = 0.04 kΩ =  Ω,  2 =   Ω,  = V                            

Unknowns:    a) V1 and        b) V2

Series circuit  formulas:

= R1 + R2                        V = I · R                        V1 = I · R1                     V2 = I · R2

Rearrange the formulas to calculate the unknowns:   I =   / 

Plug in our values:

a) R = 40 + = 100 Ω

I = V / R = / = 0.09

Notice the order in which we have solved the problem even though the first thing they ask us is V1 :

1. We calculated R because it was necessary to calculate l.

2. We calculated I because it was necessary to calculate V1 and V2

3. NOW we can calculate the potential difference between the ends of the 40 Ω resistor (V1):

V1 = I · R1 = · = 3.6 V

b) In the other resistance:  V2 = I · R2 = · = 5.4 V

Audio: 

Enable JavaScript

Creado con eXeLearning (Ventana nueva)