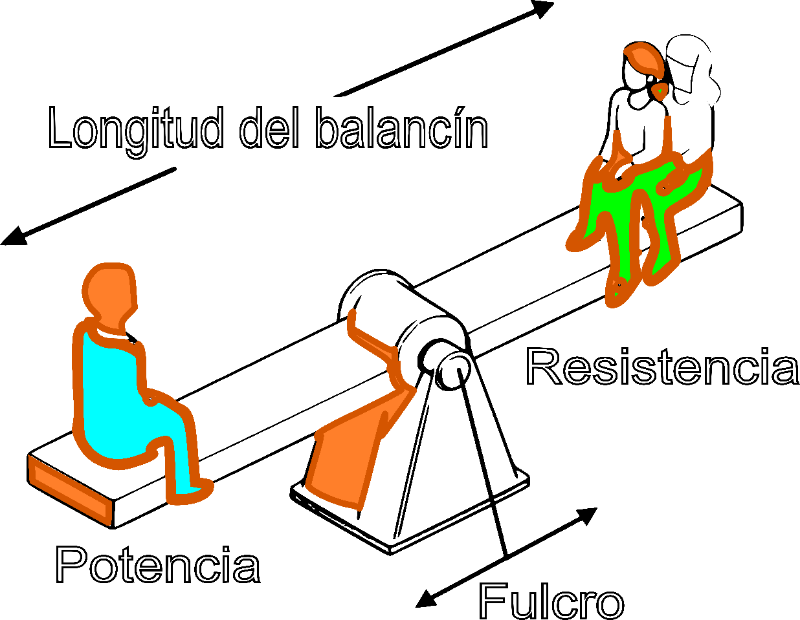Glosario

Fuerza

Definición: La fuerza es cualquiera acción o influencia que puede modificar el estado (movimiento o reposo) de un cuerpo. Normalmente se mide en Newtons (N) o kilogramos-fuerza (kgf).
Ejemplo

La caja se movió cuando le apliqué fuerza con mis brazos y piernas.

Mecanismo

Definición: Son elementos destinados a transmitir o transformar fuerzas y movimientos desde un elemento que genera el movimiento o fuerza (motor) a un elemento conducido (receptor).
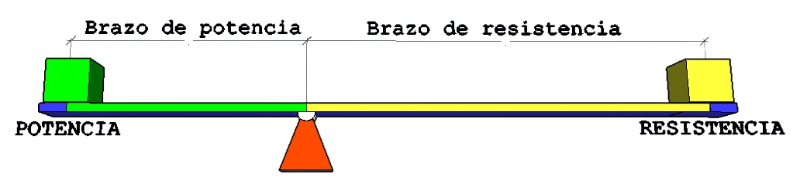
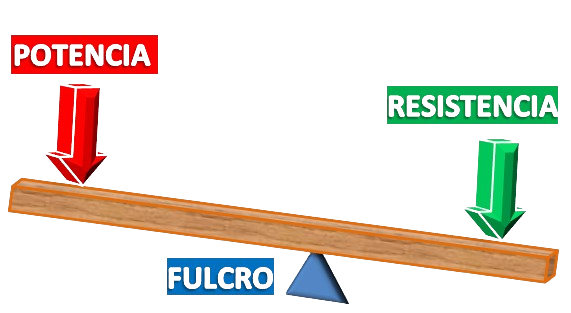
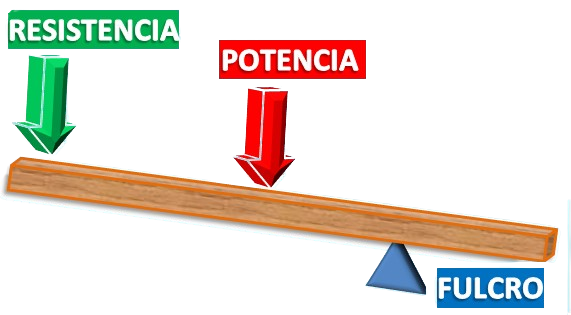
Ejemplo: La palanca es un mecanismo que me permite levantar objetos con menos esfuerzo.

Movimiento

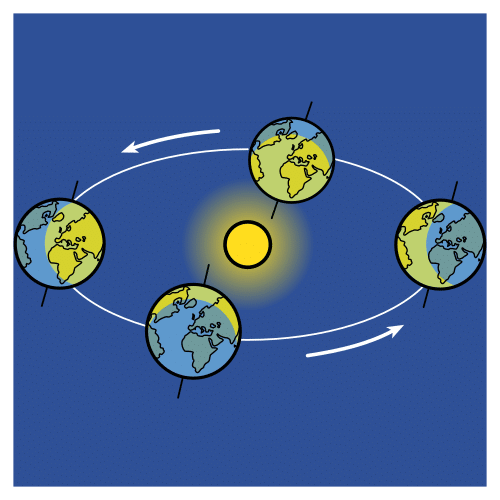
Definición: Es un cambio de posición de un cuerpo u objeto en un tiempo determinado, respecto a una referencia.
Ejemplo

La Tierra tiene un movimiento de traslación respecto al Sol.

Transmisión de movimiento

Imagen que muestra un mecanismo transmisor

Definición: El movimiento se aplica de un elemento (motor) a otro (conducido) sin cambiar el tipo de movimiento.
Ejemplo

En la bicicleta transmitimos el movimiento de los pedales a la rueda trasera mediante engranajes y una cadena.

Transformación de movimiento

Imagen que muestra un mecanismo transformador

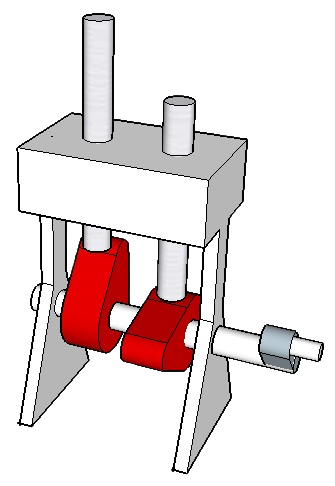
Definición: El movimiento se aplica de un elemento (motriz) a otro (conducido) cambiando el tipo de movimiento.

Ejemplo

Las cerraduras ordinarias transforman el movimiento rotatorio de la llave en uno lineal del pestillo o pasador.

Recordamos y afianzamos sobre mecanismos básicos.

Queremos que nuestras maquetas del parque biosaludable, tengan movimiento y para ello utilizaremos mecanismos.
Seguro que ya conocéis algunos mecanismos, por haberlos estudiado antes o porque observáis muchos de ellos en nuestra vida diaria (bicicleta, balancines, relojes, juguetes...).

Con los mecanismos podemos :

Cambiar la velocidad de un movimiento (aumentarla o disminuirla).
Cambiar la intensidad de una fuerza, aumentando o disminuyendo su valor.
Transformar un tipo de movimiento en otro diferente.

Haremos algunas actividades para refrescar esas ideas sobre los movimientos y mecanismos simples, que seguro habéis visto antes.

Lectura facilitada

Queremos que nuestras maquetas tengan movimiento con mecanismos.

Ya conocéis mecanismos en la bicicleta, los balancines, los relojes, los juguetes...

Con los mecanismos podemos :

Cambiar la velocidad de un movimiento a más o a menos.

Cambiar la intensidad de una fuerza, a más o a menos.

Transformar un tipo de movimiento en otro diferente.

Haremos algunas actividades sobre los movimientos y mecanismos simples.

Tipos de movimientos

Estamos viendo continuamente objetos en movimiento , pero a veces no lo analizamos.

Si lo pensamos hay cuatro movimientos básicos.

Movimiento Lineal

Movimiento rectilineo Movimiento lineal: es un movimiento en línea recta y en un solo sentido.

Ejemplo: el tren al avanzar en una recta tiene un movimiento lineal.

Imagen moviento lineal de un tren

Movimiento alternativo

Movimiento alternativo: es un movimiento de ida y vuelta, de vaivén en línea recta. Ejemplo: la aguja de una máquina de coser tiene un movimiento alternativo. Movimiento de una aguja de una máqina de coser

Movimiento rotatorio

Movimiento rotatorío Movimiento rotatorio: es un movimiento respecto a un eje de giro. Ejemplo: la rueda de un molino de agua tiene un movimiento de rotación respecto a su eje central.

Imagen moviento rueda molino

Movimiento pendular

Movimiento pendular Movimiento oscilante o pendular: es un movimiento de ida y vuelta en el arco de una circunferencia. Ejemplo: el metrónomo para música tiene un movimiento oscilante respecto a su eje.

Imagen de un metrónomo oscilante

Lectura facilitada

Si analizamos objetos en movimiento...

Podemos distinguir cuatro movimientos básicos:

movimiento lineal (el movimiento de un tren sobre la vía).
movimiento alternativo (la aguja de una máquina de coser).
movimiento rotatorio (la rueda de un molino de agua).
movimiento pendular (el movimiento del péndulo de un reloj de pared).

Plano inclinado

El plano inclinado es una superficie que forma un ángulo pequeño con el plano horizontal. Lo vemos constantemente en nuestro día a día, ya que con un plano inclinado podemos:

Subir o bajar todo tipo de cargas o elementos de un nivel bajo a un nivel más alto con menos esfuerzo. En la antigüedad, el pueblo egipcio aprendió a utilizar los planos inclinados para elevar las pesadas piedras que formaban parte de las pirámides.
Facilitar el acceso a lugares más elevados. En los edificios, disponemos de rampas (planos inclinados) que nos permiten acceder a plantas superiores o inferiores.

Imagen de un plano inclinado en una calle

Lectura facilitada

El plano inclinado es una superficie que forma un ángulo pequeño con el plano horizontal.

En los edificios disponemos de rampas para subir o bajar.

Facilitar el acceso a lugares más elevados.

Los egipcios de la antigüedad utilizaron el plano inclinado para mover las piedras de las pirámides.

Rueda

La rueda es uno de los inventos más importantes en la historia de la humanidad y consiste en un elemento mecánico de forma circular que gira alrededor de un eje central.

Con una rueda podemos:

Facilitar el transporte de todo tipo de elementos (automóvil, bicicleta, tren, carretilla), porque disminuye muchísimo el rozamiento.
Transmitir el movimiento circular en todo tipo de máquinas (noria, molino de río).

Imagen de una rueda de una bicicleta

Lectura facilitada

La rueda es uno de los inventos más importantes en la historia de la humanidad.

Es un elemento mecánico de forma circular que gira alrededor de un eje central.

Se usa para el transporte en automóviles, bicicletas, trenes, carretilla...

Se utiliza para transmitir movimiento circular en todo tipo de máquinas (noria, molino de río).

Palanca

Sin duda conocéis la palanca, una máquina simple o mecanismo que está compuesta por una barra rígida que puede girar sobre un punto de apoyo, que se llama fulcro.

La posición y la distancia de las fuerzas respecto al punto de apoyo de la palanca va a marcar su comportamiento. Para que una palanca se mantenga en equilibrio( barra en estado horizontal) se tiene que cumplir la siguiente relación:

Potencia _* Brazo de potencia = Resistencia _* Brazo de resistencia

Imagen que representa una palanca

Clasificación

Estamos rodeados de palancas y vamos a poder identificarlas según su grado (tipo de palanca en función de dónde se aplica cada fuerza y la posición del fulcro).

La clasificación de las palancas, según el grado, es la siguiente:

Primer grado
Segundo grado
Tercer grado

Primer grado

El punto de apoyo (fulcro) se encuentra entre la potencia y la resistencia.

Imagen de una palanca de primer grado Imagen de un balancín

Ejemplo: balancín.

Segundo grado

La resistencia se encuentra entre la potencia y el punto de apoyo.

Imagen de una palanca de segundo grado Imagen de una carretilla

Ejemplo: carretilla.

Tercer grado

La potencia se encuentra entre la resistencia y el punto de apoyo.

Imagen de una palanca de tercer grado Imagen de unas pinzas

Ejemplo: pinzas de depilar.

¿Tenéis dudas con las palancas?

Vamos con un ejemplo: Imagen de una balancín con sus elementos como palanca

Se desean equilibrar los pesos entre el alumnado de una clase de 1º ESO.

Alberto pesa 60 kg, Antía pesa 45 kg y Sabela también pesa 45 kg.

La barra del balancín mide 3 metros. Antía y Sabela están sentadas a 1 metro del punto de apoyo.

¿A qué del punto de apoyo (fulcro) se debe sentar Alberto si queremos equilibrar su peso con la suma del peso de Antía y de Sabela?.

Resolvemos:

Potencia _* Brazo de potencia = Resistencia _* Brazo de resistencia

Peso de Alberto _* distancia de Alberto al fulcro = Suma de pesos de Antía y Sabela _* distancia de Antía y Sabela al fulcro

60 kg _* distancia de Alberto al fulcro = (45 kg + 45 kg) _* 1 m

Distancia \, de\, Alberto\, al\, fulcro\, = \,\frac{90 kg\, * \,1 m}{60 kg} \, = \, 1,5 \,m

Por lo tanto, si Antía y Sabela están sentadas a 1 metro del punto de apoyo, Alberto debe sentarse a 1 metro y medio para mantener la barra horizontal (barra en equilibrio).

Pinchando en el siguiente enlace, simulador de una palanca o en la imagen inferior, podéis utilizar este interesante recurso para hacer pruebas de funcionamiento de un balancín (palanca de primer grado):

Lectura facilitada

Ejemplo:

Equilibrar los pesos entre varios alumnos.

Alberto pesa 60 kg.

Antía pesa 45 kg.

Sabela también pesa 45 kg.

La barra del balancín mide 3 metros.

Antía y Sabela están sentadas a 1 metro del punto de apoyo.

¿A qué distancia del el punto de apoyo se debe sentar Alberto para equilibrar el balancín?

Ten en cuenta la suma de los pesos de Antía y Sabela.

Resolvemos:

Potencia * Brazo de potencia = Resistencia * Brazo de resistencia

Peso de Alberto * distancia de Alberto al fulcro = Suma de pesos de Antía y Sabela * distancia de Antía y Sabela al fulcro

60 kg * distancia de Alberto al fulcro = (45 kg + 45 kg) * 1 m

Distancia \, de\, Alberto\, al\, fulcro\, = \,\frac{90 kg\, * \,1 m}{60 kg} \, = \, 1,5 \,m

Por lo tanto, Alberto debe sentarse a 1 metro y medio para mantener el balancín en equilibrio.

Pincha en la imagen para simular y experimentar en el laboratorio de equilibrio.