¿Y las áreas?
Prismas
 Escalado a 1:2
Escalado a 1:2 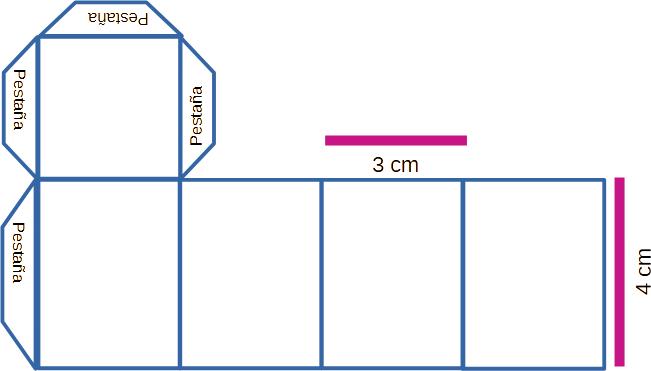
Si reduces la arista a la mitad, ¿cuántos prismas pequeños se pueden hacer en una cartulina DIN A4?
Para contestar esta pregunta, toca hablar de áreas.
Repaso de áreas...
Recuerda que el área es la medida del interior de una figura plana.
El curso pasado viste la fórmula del área del rectángulo = base x altura
Y que la del triángulo era la mitad = \( \large\frac{base\text{ } \times\text{ } altura}{2}\)
Si tienes otras figuras, como rombos, trapecios... puedes descomponerlas en triángulos y aplicar la fórmula anterior.
Al lío...
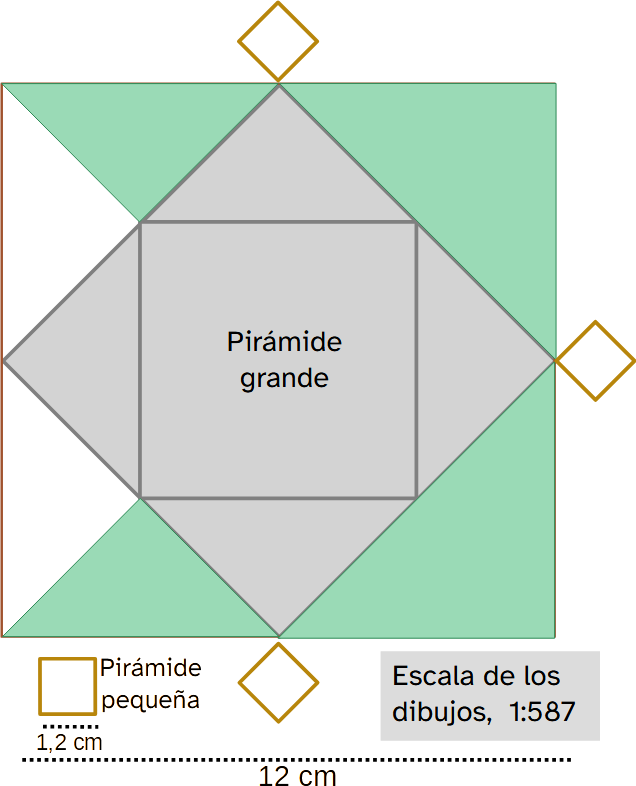
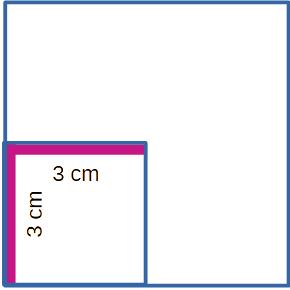 Observa el cuadrado pequeño, tiene de lado la mitad del grande.
Observa el cuadrado pequeño, tiene de lado la mitad del grande.
Calcula su área 3 x 3 = 6 cm2.
Calcula el área del grande 6 x 6 = 36 cm2.
¿Qué ocurre?
36 ÷ 6 = 4; el área pequeña es la cuarta parte de la grande.
Parece que si el lado es la mitad, el área es la cuarta parte.
¿Y esto pasa siempre?
Otro lío...
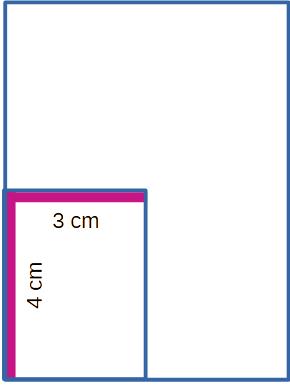 Sí, esto pasa siempre.
Sí, esto pasa siempre.
Como el área es base x altura, si haces la mitad de cada lado, en el área se aplica la mitad por la mitad, la cuarta parte.
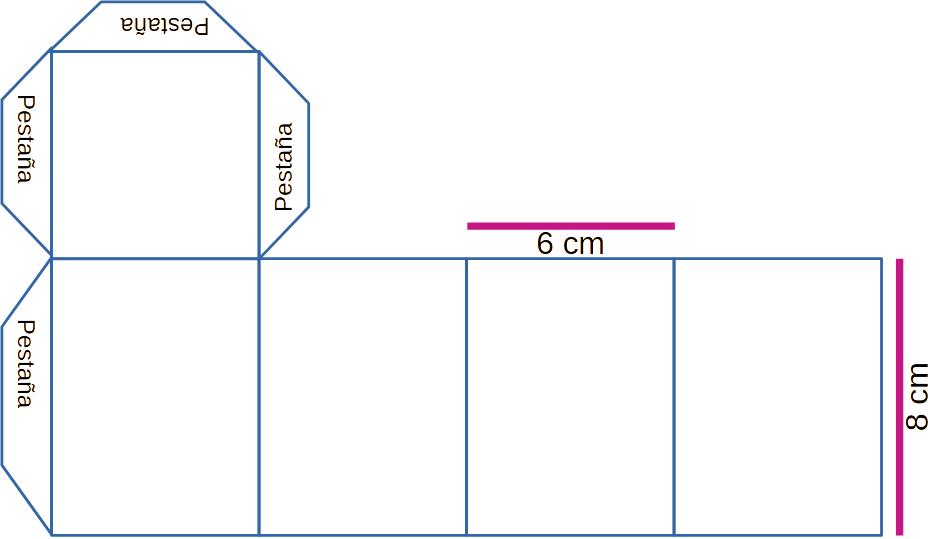
Área del pequeño 4 x 3 = 12 cm2.
Calcula el área del grande 8 x 6 = 48 cm2.
48 ÷ 12 = 4
Así que, con una cartulina del mismo tamaño podrás dibujar 4 desarrollos planos.
Si quieres descargar este modelo y los reducidos, puedes utilizar el archivo que está a continuación.
El archivo
Descarga el archivo en PDF con los modelos grande y pequeños, haciendo clic sobre la imagen.


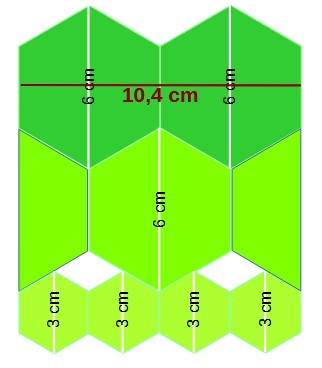 Calculad las áreas de cada una de las figuras que forman la base del bote.
Calculad las áreas de cada una de las figuras que forman la base del bote.