Creando movimientos
Movimiento
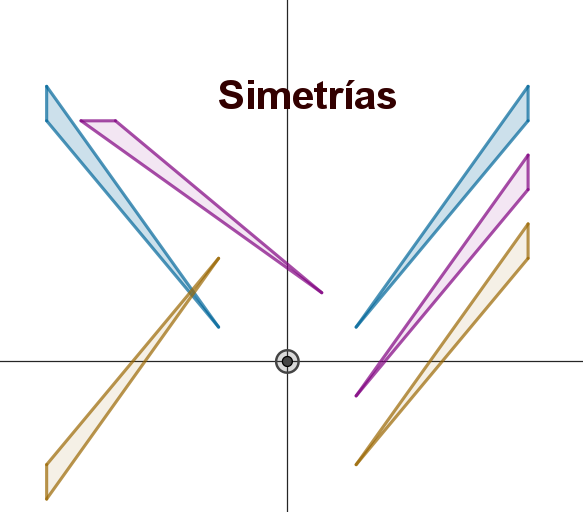Las simetrías, son movimientos de figuras que conservan su tamaño y su forma.
Te pueden resultar muy útiles para hacer tu composición artística.
El curso pasado ya viste que cualquier figura puede moverse con una traslación, un giro o una reflexión.
Estas tres simetrías: respecto a un vector, a un centro, o a un eje, son las que vas a repasar.
Vas a empezar por el más sencillo, la traslación, luego verás el giro y finalmente la reflexión.
Traslación
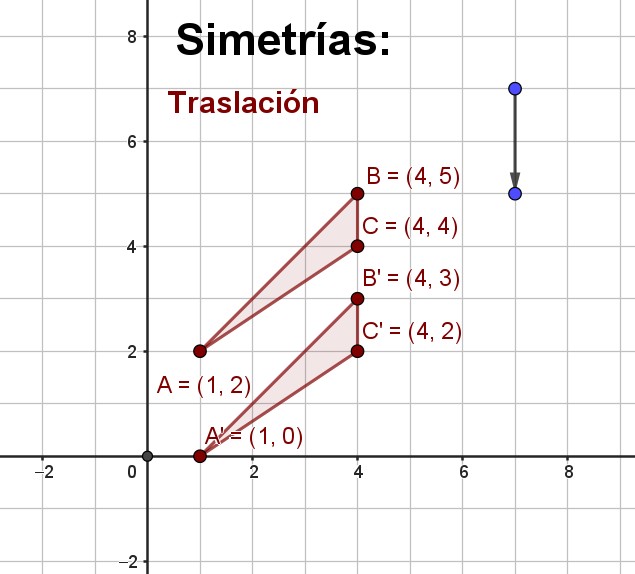Observa el triángulo de la imagen: ABC.
Lo vas a mover dos unidades hacia abajo.
Esa dirección y sentido se indica con una flecha, un vector, como la del dibujo.
Lo más fácil es ponerlo sobre una cuadrícula e ir moviendo sus vértices según la flecha.
Estás haciendo una traslación de vector (0,2); 0 en horizontal y 2 en vertical.
Observa cómo han quedado las coordenadas de los puntos al trasladar:
A = (1,2) pasa a ser A' = (1,0) ¿Por qué crees que ocurre esto?
Escribe la respuesta en tu cuaderno.
Giro
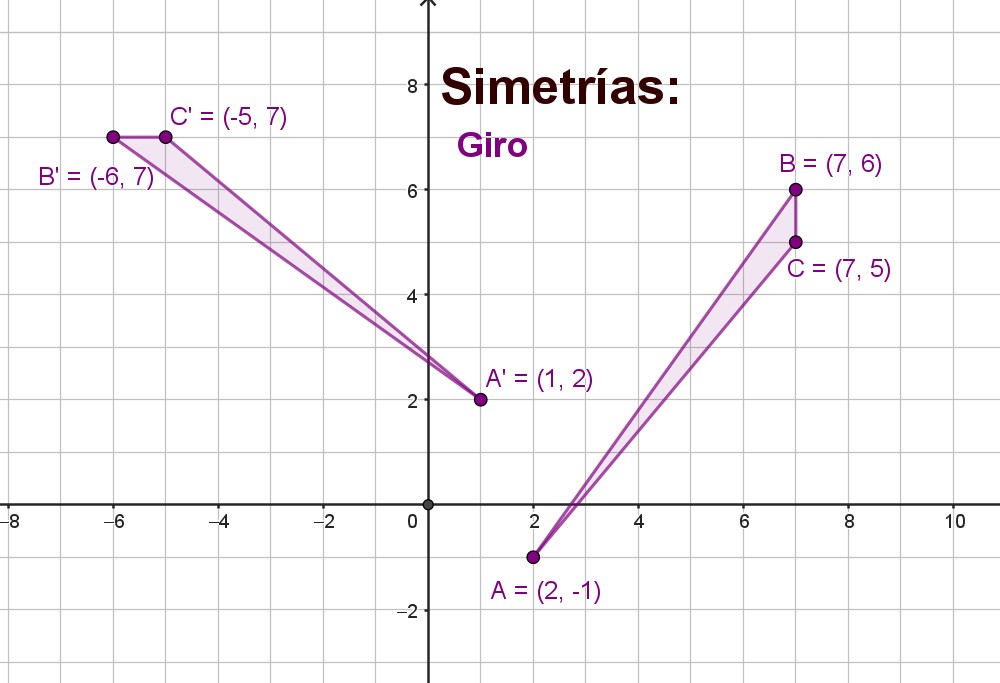
Observa el triángulo de la imagen: ABC.
Lo vas a girar un ángulo de 90º.
También necesitas tener un centro de giro, va a ser el (0,0).
Y un sentido, será el contrario a las agujas del reloj (antihorario).
El giro es un movimiento que tiene como elementos importantes un centro y un ángulo orientado.
El giro también se llama rotación.
Observa cómo han quedado las coordenadas de los puntos al girar:
A = (2,-1) pasa a ser A' = (1,2) ¿Por qué crees que ocurre esto?
Escribe la respuesta en tu cuaderno.
Giro de 180º
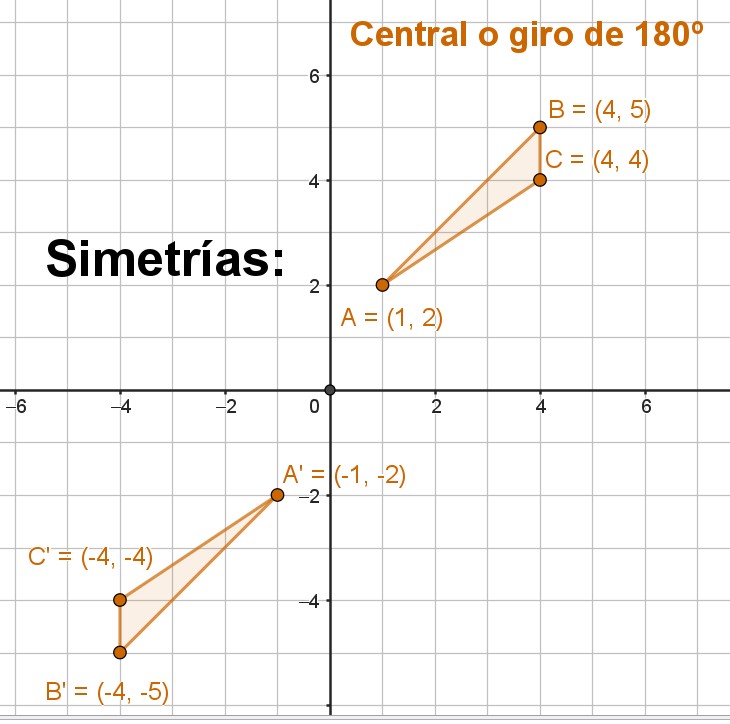Un ejemplo de giro muy especial es el giro de 180º.
A este tipo de giro se le da el nombre de "simetría central".
En el dibujo al triángulo ABC se le ha dado un giro de 180º, con centro el (0,0).
Observa cómo han quedado las coordenadas de los puntos al girar:
A = (1,2) pasa a ser A' = (-1,-2) ¿Por qué crees que ocurre esto?
Escribe la respuesta en tu cuaderno.
Reflexión
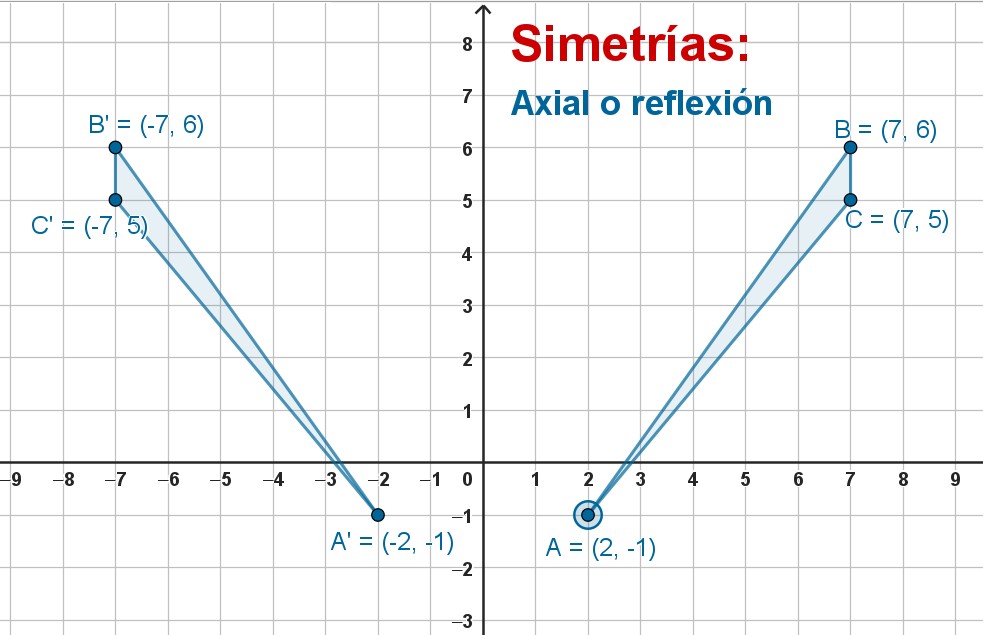Este movimiento es el más complicado porque consiste en hacer un "efecto espejo".
La reflexión, o simetría axial, es un movimiento que coloca la figura original y la reflejada a la misma distancia de un segmento, el eje de reflexión.
Observa cómo han quedado las coordenadas de los puntos al reflejarse:
A = (2,-1) pasa a ser A' = (-2,-1) ¿Por qué crees que ocurre esto?
Escribe la respuesta en tu cuaderno.
¿Materiales?
Para crear movimientos es útil el papel vegetal.
Si marcas un eje de simetría y doblas por él, puedes visualizar como quedará la figura reflejada.
Luego calcas con lápiz y la repasas.
También puedes darle la vuelta, y hacer así el efecto espejo.
Para traslaciones o giros, calca y haz el movimiento.
Si prefieres hacerlo con el ordenador, utiliza un programa de dibujo, como Draw o Gimp; o geométrico como GeoGebra.
Todos ellos tienen botones específicos para movimientos (busca: girar, rotar, voltear, reflejar...).
Lectura facilitada
Las simetrías, son movimientos de figuras.
Conservan su tamaño y su forma.
Te ayudarán a hacer el cuadro.
Hay tres: traslación, giro y reflexión.
Estas tres simetrías:
respecto a un vector, a un centro, o a un eje, son las que vas a repasar.
