Glosario
Emblemático
-
Definición:
-
Sinónimo de representativo.
-
Ejemplo:
-
Un edificio emblemático de Galicia es la Catedral de Santiago.
ReMates y ReTales
3.7. Diseñadoras por un día
Bocetos y diseños
¿Has visto algún boceto diseño de una prenda de ropa?
Muchas veces son verdaderas obras de arte.
Normalmente la elección de las proporciones del boceto es libre, pero en moda generalmente se utiliza el "método de las nueve cabezas", de forma que la altura es directamente proporcional a la longitud de la cabeza, concretamente la altura es nueve veces la longitud de la cabeza.
Para producir prendas de ropa resulta de vital importancia disponer de una serie de proporciones humanas, pues a partir de unas medidas se deducen proporcionalmente el resto. Por ejemplo, las medidas de cada parte de una camisa vienen dadas por la medida del cuello.
A la hora de realizar un dibujo, una pieza de arte o una obra arquitectónica, seguir unas proporciones determinadas influye en la belleza del resultado final, como la proporción áurea, las proporciones de Vitrubio o las proporciones de Le Corbusier.
Lectura facilitada
Los bocetos de diseño de ropa pueden ser obras de arte.
Usan el "método de las nueve cabezas":
la altura es nueve veces la longitud de la cabeza.
A partir de unas medidas se deducen proporcionalmente el resto.
Semejanza
Hemos trabajado anteriormente con las proporcionalidades. En geometría, la semejanza representa proporcionalidad entre figuras y cuerpos.
Dos figuras son semejantes cuando se diferencian en tamaño, pero no en forma. En dos figuras semejantes el cociente entre la distancia entre dos puntos de una figura y la distancia entre los dos mismos puntos de la segunda figura siempre da el mismo resultado.
Por ejemplo, estos dos bolsos de tela son semejantes:
Polígonos semejantes
Dos polígonos son semejantes si tienen los ángulos iguales y los lados correspondientes son proporcionales.
Al cociente entre el lado de un polígono y el correspondiente del otro polígono se llama razón de semejanza.
La razón de semejanza es la constante de proporcionalidad que guardan las medidas de sus lados.
Por ejemplo, estos dos polígonos son semejantes y su razón de semejanza es \( \dfrac{7}{10}=\dfrac{1,4}{2}=0,7\):
Cuando la razón es 1 se dice que las figuras son congruentes (serían dos figuras idénticas).
Triángulos semejantes
A la hora de estudiar la semejanza entre triángulos, existen unos criterios que nos permiten simplificar la definición de polígonos semejantes.
Criterio 1
Dos triángulos son semejantes si sus lados son proporcionales:
\( \dfrac{\overline{AB}}{\overline{A'B'}}=\dfrac{\overline{BC}}{\overline{B'C'}}=\dfrac{\overline{AC}}{\overline{A'C'}}\)
Criterio 2
Dos triángulos son semejantes si tienen dos ángulos iguales:
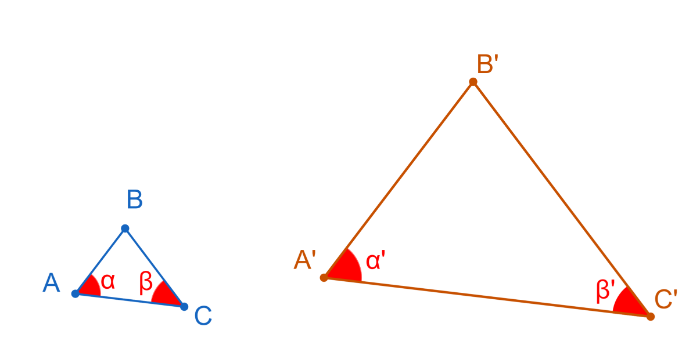
\( \alpha = \alpha' \quad\) y \( \quad\beta= \beta' \)
Criterio 3
Dos triángulos son semejantes si tienen dos lados proporcionales e igual el ángulo que forman:
\( \alpha = \alpha' \quad\) y \(\quad\dfrac{\overline{AB}}{\overline{A'B'}}=\dfrac{\overline{AC}}{\overline{A'C'}}\)
Vestidos semejantes
Observa
Observa este GeoGebra detenidamente. Verás cómo un vestido se transforma al cambiar el valor de la razón de semejanza, k.
Experimenta
Prueba qué ocurre para diferentes valores de k.
Fíjate, especialmente, qué sucede cuando:
- k es mayor que 1, k > 1.
- k es menor que 1, k < 1.
Reflexiona
- ¿Cambia el tamaño del vestido cuando k es mayor que 1? ¿Se hace más grande o más pequeño?
- ¿Y cuando k es menor que 1?
- ¿Qué ocurre exactamente con la forma del vestido en cada caso? ¿Se mantiene igual o se altera?
- ¿Podrías describir con tus propias palabras qué representa la razón de semejanza, k?
https://www.geogebra.org/m/dvaempbm (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
La tela gemela
Imagina que quieres hacer dos prendas de ropa de dos tallas distintas, pero con la misma forma.
¿Cómo es posible saber si dos telas o dos retales son semejantes?
En esta actividad, pondrás a prueba tu capacidad de observación y medida para descubrir las semejanzas entre distintos trozos de tela.
https://www.geogebra.org/m/wswasguj (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
Autoría: GeoGebra Content Team
Razones para diseñar
Calcula la razón de semejanza entre estas telas.
https://www.geogebra.org/m/btph9dq5 (Ventana nueva)
Actividad%20no%20completada,Actividad%20superada.%20Puntuaci%F3n%3A%20%25s,Actividad%20no%20superada.%20Puntuaci%F3n%3A%20%25s,Guardar%20la%20puntuaci%F3n
Autoría: GeoGebra Content Team
El desfile de moda
En tu ayuntamiento quieren colgar una pancarta enorme para anunciar un desfile de moda sostenible de diseñadoras y diseñadores de Galicia.
Te piden ayuda para calcular la longitud de la pancarta. Puedes medir la base del edificio del ayuntamiento pero no conoces su altura.
No te preocupes, las matemáticas pueden ayudarte. Ahora que conoces los criterios de semejanza de triángulos seguro que puedes resolverlo.
En un día soleado, calculas la sombra del edificio, que es de 4 metros. En el mismo instante, la sombra de una persona que es de 0,5 metros. Esa persona mide 1,65 metros.
- ¿Puedes calcular la altura del edificio?
- Si la pancarta tiene que quedar a 2 metros del suelo, ¿qué longitud máxima puede tener?
¡Manos a la obra!
Realizar un diseño, ya sea de una prenda de ropa, una maqueta, un cartel, una postal... requiere elaborar previamente un boceto.
Investiga en internet distintos diseños de bolsa que puedan inspirarte. Sigue los siguientes consejos para realizar una búsqueda segura y eficiente en internet:
- Cuando vayas a acceder a una página web comprueba que su dirección comience por HTTPS.
- Cuando utilices un buscador, utiliza palabras clave. No escribas frases largas.
- No te quedes con la información de una única fuente. Busca más ideas para combinar e inspirarte.
Una vez estés inspirado/a es hora de hacer varios bocetos. No tienen por qué estar muy bien dibujados, no es necesario poner las medidas ni que sean proporcionales a la realidad. El objetivo es plasmar varias ideas hasta que finalmente encuentres la que más te gusta.
Entre todos los bocetos que has diseñado seguro que has encontrado la idea que más te inspira. Ahora es el momento de hacer el diseño definitivo. Dibuja la bolsa e incluye el diseño que vas a realizar con los retales:
- ¿Cómo utilizarás los retales para configurar la bolsa?
- ¿Elaborarás algún dibujo a partir de los retales de tela reciclados?
- ¿Incluirás un dibujo a mano con ayuda de un rotulador para ropa?
- ¿Harás un bordado?
¡Hay muchísimas opciones! A continuación, te dejamos varias ideas.
Con trozos de tela triangulares puedes representar una grulla de origami:
Otra opción es utilizar cuadriláteros para representar un cubo de Rubik:
Podemos utilizar los retales para dibujar diferentes figuras, como un Sol:
Con piezas de tela puedes fabricar bolsillos de distintos tamaños: para tus bolígrafos, para la cartera, para la agenda...
La distribución de los retales también puede dar lugar a distintas configuraciones de bolsa.
¿Utilizarás los mismos colores en los mismos sitios?
¿Crearás un patrón en zigzag?
¿Y las asas? Pueden ser cortas, largas, de los dos tipos, una única asa...
¡Deja volar tu imaginación!
Áreas semejantes
Imagina que has elegido incluir un sol en tu bolsa.
El boceto tiene como diámetro del círculo central del sol 15 cm, pero en la realidad este será de 2,5 veces mayor.
¿Sabes cómo calcular el área de los trozos de tela a partir del boceto?
Recalculando...
Se te han ocurrido dos formas de hacer las operaciones.
Método 1:
- Como el diámetro del patrón es de 15 cm, el diámetro en la realidad será de \(15 \cdot 2,5 = 37,5\) cm.
- El área del círculo central de la tela será de \( \pi \cdot 18,75^2 = 1 104 \) cm2.
Método 2:
- Como el diámetro en el patrón es de 15 cm, el área en este será de \( \pi \cdot 7,5^2 = 176,71 \) cm2.
- El área del círculo central en la tela será de \(176,71 \cdot 2,5 = 441,775\) cm2.
¡Algo pasa aquí! Los dos números no coinciden...
¿Cuál es la forma correcta?
Razón de las áreas
El boceto y la figura a recortar en la tela son semejantes, pero la razón entre sus medidas longitudinales no es la misma que la de sus medidas de áreas, puesto que al hallarlas pasamos a una dimensión cuadrática.
Si dividimos las áreas entre sí, obtenemos el cuadrado de la razón de las longitudes.
- En el ejemplo anterior el método 1 es correcto.
- El método 2 también es válido si multiplicamos por la razón al cuadrado, es decir:
\( 176,71 \cdot 2,5^2 = 1 104\) cm2.
El diseño definitivo
Ahora que ya tienes tu boceto, es hora de realizar el diseño definitivo de tu bolsa de tela.
Telas
Ya has visto la importancia de las proporciones en la moda, arte y arquitectura.
¡Tú diseño también esconderá un secreto matemático!
Recuerda que en la fase 3.4. Huella de carbono pensaste en las dimensiones de los retales de las prendas recicladas.
La recomendación es que, para facilitar los cálculos la composición final de la bolsa, cortes rectángulos todos del mismo tamaño. Pero si tu equipo y tú os animáis, hay infinidad de otras opciones posibles.
¿Qué relación vas a elegir entre el ancho y el largo de los retales de ropa?
Decide qué proporción cumplirán los retales de tu bolsa de tela: proporción áurea, proporción de plata, proporción cordobesa...
Bolsa
Pero no solo los retales tienen que ser proporcionales.
Si quieres ir un paso más allá, te dejamos algunas ideas para hacer tu bolsa proporcional:
- El ancho de la bolsa proporcional a la longitud de tu mano.
- El alto de la bolsa proporcional a tu altura.
- La bolsa y su bolsillo son proporcionales.
Diseña
¡Ya tienes todos los ingredientes! Es hora de ponerte manos a la obra. Realiza el diseño e incluye:
- Una vista frontal de la bolsa.
- Una vista trasera.
- Las medidas que tendrá en la realidad.
- El área de cada una de las piezas de tela que necesitarás para hacer la bolsa y su etiqueta. Utilizando la razón de semejanza entre áreas de dos figuras proporcionales.
Elige
Para crear el diseño puedes emplear distintos medios:
- Puedes hacer el diseño a mano sobre papel blanco o papel milimetrado utilizando lápiz, goma, regla, escuadra y cartabón, compás...
- Si en tu centro contáis con ordenadores E-Dixgal, puedes hacer el diseño ayudándote de tu ordenador, por ejemplo utilizando las aplicaciones FreeCad, KolourPaint, Inkscape, recursos web seguros...
- Si en tu centro disponéis de Polos Creativos, puedes hacer el diseño ayudándote de una tableta.
Ficha
Tienes a tu disposición una ficha de trabajo en equipo en formato editable y pdf para ayudarte.
Recuerda descargar la ficha en formato editable con el botón derecho del ratón.
Definiciones
- Figuras semejantes
-
Dos figuras son semejantes si el cociente entre la distancia entre dos puntos de una figura y la distancia entre los dos mismos puntos de la segunda figura siempre da el mismo resultado.
- Polígonos semejantes
-
Dos polígonos son semejantes si tienen los ángulos iguales y los lados correspondientes son proporcionales.
Al cociente entre el lado de un polígono y el correspondiente del otro polígono se llama razón de semejanza.
La razón de semejanza es la constante de proporcionalidad de las medidas de los lados.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0