3.5. Condiciones laborales

Glosario

Ecosistema

Definición:: Un ecosistema está formado por el conjunto de seres vivos que habitan un lugar determinado y el medio en el que habitan. (Fuente: RAE)
Ejemplo:: Un bosque es un ecosistema terrestre.

Inversión

Definición:: En economía, una inversión consiste en utilizar los recursos disponibles para aumentar la producción o las ganancias.
Ejemplo:: En una fábrica, invertir en máquinas más modernas permite aumentar la producción de prendas.

Precario

Definición:: Poco estable.
Ejemplo:: Muchos jóvenes tienen trabajos precarios, con contratos temporales y bajos salarios.

Tomando conciencia

La industria de la moda rápida, no solo tiene un impacto negativo en el ecosistema, sino también en las personas que trabajan en ella.

Más adelante verás, en el apartado 3.9. Productos de proximidad, que la mayor parte de estas industrias están localizadas en unos países concretos. Seguro que muchos ya los conoces por la actividad que hiciste en el apartado 1.2. Un reto sostenible.

¿Crees que en esos países las condiciones de trabajo son las mismas que en Galicia?

Lectura facilitada

La moda rápida influye en las personas que trabajan en ella.

Estas industrias están localizadas en unos países concretos.

¿Piensas que las condiciones de trabajo son las mismas que en Galicia?

Trabajando en la industria

Tres en raya La industria de la moda rápida se basa en producir muchísimas prendas en muy poco tiempo.

En este proceso intervienen muchas magnitudes que ahora vas a analizar.

Empezamos por un caso sencillo con tres magnitudes.

Todas para una

Y una para todas...

Hilos enhebrados juntos en la misma agua En el estudio de varias magnitudes, siempre hay una de ellas que ejerce el papel principal y otras que hacen un papel secundario.

La comparación se hace por parejas, combinando siempre la magnitud principal con cada una de las demás.

En ese proceso, a las magnitudes que no forman parte de la comparación se les asigna un valor fijo (no cambian).

Se trata de un estudio de proporcionalidad compuesta.

Las tres magnitudes

Veamos un ejemplo.

Vamos a comparar el número de personas empleadas en una fábrica de camisetas con:

el número de camisetas producidas y
el número de horas que tardan en fabricarlas.

Se trata de un estudio de proporcionalidad compuesta en el cual intervienen tres magnitudes.

Composición de tres en raya con personas, camisetas y horas. El número de personas empleadas es la magnitud principal.

Hacemos la comparación con cada una de las otras dos.

Si el número de horas queda fijo, el doble de personas fabricarán el doble de camisetas (proporcionalidad directa).
Si el número de camisetas queda fijo, el doble de personas necesitará la mitad de horas (proporcionalidad inversa).

Visualiza: ¿comparado con...?

Si 100 personas trabajando pueden producir 500 camisetas a la última moda en 3 horas:

¿Cuántas personas serán necesarias para producir 1000 camisetas en 5 horas?
¿Cuántas horas tendrán que trabajar 150 personas para producir 2000 camisetas?
¿Cuántas camisetas se podrán producir con 200 personas trabajando en 2 horas?

Observa que en cada una de las preguntas se compara una magnitud con otras dos.

Cada pregunta da lugar a un estudio de proporcionalidad compuesta diferente.

Lo primero es escribir una tabla:

Personas

Número de personas	Número de camisetas	Número de horas
100	500	3
x	1000	5

Identificamos la magnitud principal que viene dada por la pregunta que tenemos que responder, es el número de personas que trabajan en la producción.

Composición de tres en raya con personas, horas y camisetas.

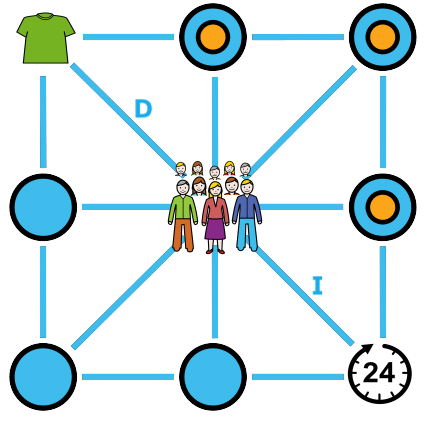
Ya vimos que:

N.º de personas y n.º de camisetas guardan una relación de proporcionalidad directa.
N.º de personas y n.º de horas de trabajo guardan una relación de proporcionalidad inversa.

Si la relación entre magnitudes es inversamente proporcional debe utilizarse la fracción inversa.

Por lo tanto, la relación debe escribirse:

\( \dfrac{100}{x} = \dfrac{500}{1000} \cdot \textcolor{red}{\dfrac{5}{3}}\)

Despejando x obtenemos:

\(x = \dfrac{1000\cdot100\cdot 3}{500\cdot 5} = 120\)

Serán necesarias 120 personas para producir 1000 camisetas en 5 horas.

Horas

Número de personas	Número de camisetas	Número de horas
100	500	3
150	2000	x

Identificamos la magnitud principal que viene dada por la pregunta que tenemos que responder, es el número de horas que trabajan en la producción.

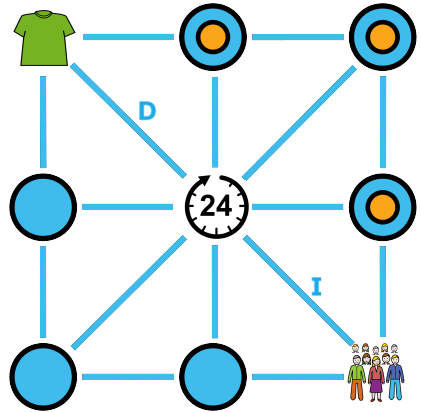Composición de tres en raya con horas, personas y camisetas. Hacemos las comparaciones:

N.º de horas trabajadas y n.º de camisetas a producir con una cantidad fija de personas trabajando, guardan una relación de proporcionalidad directa.
N.º de horas trabajadas y n.º de personas necesarias para producir una cantidad fija de camisetas, guardan una relación de proporcionalidad inversa.

Si la relación entre magnitudes es inversamente proporcional debe utilizarse la fracción inversa.

Por lo tanto, la relación debe escribirse:

\( \dfrac{3}{x} = \dfrac{500}{2000} \cdot \textcolor{red}{\dfrac{150}{100}}\)

\(x = \dfrac{3\cdot2000\cdot 100}{5000\cdot 150} = 8\)

Tendrán que trabajar 8 horas para producir 2000 camisetas.

Camisetas

Número de personas	Número de camisetas	Número de horas
100	500	3
200	x	2

Identificamos la magnitud principal que viene dada por la pregunta que tenemos que responder, es el número de camisetas fabricadas.

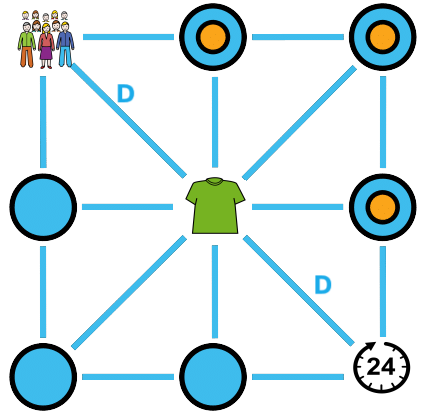Composición de tres en raya con camisetas, personas y horas. Hacemos las comparaciones:

N.º de camisetas fabricadas y n.º de personas necesarias dejando fijo el tiempo que trabajan, guardan una relación de proporcionalidad directa.
N.º de camisetas fabricadas y n.º de horas trabajando una cantidad fija de personas, guardan una relación de proporcionalidad directa.

Por lo tanto, la regla de tres directa debe escribirse:

\( \dfrac{500}{x} = \dfrac{100}{200} \cdot\dfrac{3}{2}\)

\(x = \dfrac{500\cdot200\cdot 2}{100\cdot 3} \simeq 667\)

Se podrán producir 667 camisetas.

Es tu turno

Lee el texto y completa las palabras que faltan.

%E9%B0%E6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%D1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FB%FC%E1%E6%E0%E7%F1%E6%FB%FD%FC%E1%B0%A8%B0%AE%E2%AC%DE%F7%F7%B2%F7%FE%B2%E6%F7%EA%E6%FD%B2%EB%B2%F1%FD%FF%E2%FE%F7%E6%F3%B2%FE%F3%E1%B2%E2%F3%FE%F3%F0%E0%F3%E1%B2%E3%E7%F7%B2%F4%F3%FE%E6%F3%FC%BC%AE%BD%E2%AC%B0%BE%B0%E6%F7%EA%E6%C6%F7%EA%E6%B0%A8%B0%B7%A1%D1%E2%B7%A1%D7%C6%E7%B7%A0%A2%F7%E3%E7%FB%E2%FD%B7%A0%A2%EB%F3%B7%A0%A2%E1%F7%B7%A0%A2%FA%F3%B7%A0%A2%E2%E7%F7%E1%E6%FD%B7%A0%A2%FF%F3%FC%FD%E1%B7%A0%A2%F3%B7%A0%A2%FE%F3%B7%A0%A2%FD%F0%E0%F3%B7%A0%A2%E2%F3%E0%F3%B7%A0%A2%F1%E0%F7%F3%E0%B7%A0%A2%FE%F3%B7%A0%A2%F0%FD%FE%E1%F3%BC%B7%A0%A2%C2%F3%E0%F3%B7%A0%A2%F1%FD%FC%E1%F7%F5%E7%FB%E0%B7%A0%A2%EB%B7%A0%A2%E2%E0%F7%E2%F3%E0%F3%E0%B7%A0%A2%A0%A2%B7%A0%A2%E6%E0%FD%E8%FD%E1%B7%A0%A2%F6%F7%B7%A0%A2%E6%F7%FE%F3%B7%A0%A2%E0%F7%F1%FB%F1%FE%F3%F6%FD%E1%B7%A0%A2%FA%F3%F0%B7%D7%AB%FB%E1%B7%A0%A2%FC%F7%F1%F7%E1%FB%E6%F3%F6%FD%B7%A0%A2%A1%B7%A0%A2%F6%B7%D7%D6%F3%E1%B7%A0%A2%F6%F7%B7%A0%A2%F0%B7%D4%D3%E1%E3%E7%F7%F6%F3%B7%A0%A2%EB%B7%A0%A2%E6%E0%F3%F0%F3%F8%FD%BC%B7%D3%A2%B7%A1%D1%BD%E2%B7%A1%D7%B7%A2%D3%B7%A1%D1%E2%B7%A1%D7%C4%E7%F7%E1%E6%E0%FD%B7%A0%A2%F7%E3%E7%FB%E2%FD%B7%A0%A2%F7%E1%E6%B7%D7%A3%B7%A0%A2%F4%FD%E0%FF%F3%F6%FD%B7%A0%A2%E2%FD%E0%B7%A0%A2%F1%E7%F3%E6%E0%FD%B7%A0%A2%E2%F7%E0%E1%FD%FC%F3%E1%B7%A0%D1%B7%A0%A2%FE%F3%B7%A0%A2%E0%F7%FE%F3%F1%FB%B7%D4%A1%FC%B7%A0%A2%F6%F7%B7%A0%A2%E2%E0%FD%E2%FD%E0%F1%FB%FD%FC%F3%FE%FB%F6%F3%F6%B7%A0%A2%F7%FC%E6%E0%F7%B7%A0%A2%F7%FE%B7%A0%A2%FC%B7%D4%D3%FF%F7%E0%FD%B7%A0%A2%F6%F7%B7%A0%A2%FB%FC%E6%F7%F5%E0%F3%FC%E6%F7%E1%B7%A0%A2%F6%F7%FE%B7%A0%A2%F7%E3%E7%FB%E2%FD%B7%A0%A2%EB%B7%A0%A2%FE%FD%E1%B7%A0%A2%E6%E0%FD%E8%FD%E1%B7%A0%A2%F6%F7%B7%A0%A2%E6%F7%FE%F3%B7%A0%A2%F1%FD%FC%E1%F7%F5%E7%FB%F6%FD%E1%B7%A0%A2%F7%FC%B7%A0%A2%A1%B7%A0%A2%F6%B7%D7%D6%F3%E1%B7%A0%A2%F7%E1%B7%A0%A2%D2%D2%F6%FB%E0%F7%F1%E6%F3%FF%F7%FC%E6%F7%D2%D2%B7%A0%A2%E2%E0%FD%E2%FD%E0%F1%FB%FD%FC%F3%FE%BC%B7%A0%A2%C1%FB%FC%B7%A0%A2%F7%FF%F0%F3%E0%F5%FD%B7%A0%D1%B7%A0%A2%F7%FE%B7%A0%A2%FC%B7%D4%D3%FF%F7%E0%FD%B7%A0%A2%F6%F7%B7%A0%A2%E2%F7%E0%E1%FD%FC%F3%E1%B7%A0%A2%E3%E7%F7%B7%A0%A2%F4%FD%E0%FF%F3%FC%B7%A0%A2%F7%FE%B7%A0%A2%F7%E3%E7%FB%E2%FD%B7%A0%A2%EB%B7%A0%A2%FE%FD%E1%B7%A0%A2%F6%B7%D7%D6%F3%E1%B7%A0%A2%E3%E7%F7%B7%A0%A2%E1%F7%B7%A0%A2%FA%F3%FC%B7%A0%A2%E6%F3%E0%F6%F3%F6%FD%B7%A0%A2%F7%FC%B7%A0%A2%F1%FD%FC%E1%F7%F5%E7%FB%E0%B7%A0%A2%A0%A2%B7%A0%A2%E6%E0%FD%E8%FD%E1%B7%A0%A2%E1%FD%FC%B7%A0%A2%D2%D2%FB%FC%E4%F7%E0%E1%F3%FF%F7%FC%E6%F7%D2%D2%B7%A0%A2%E2%E0%FD%E2%FD%E0%F1%FB%FD%FC%F3%FE%F7%E1%BC%B7%D3%A2%B7%A1%D1%BD%E2%B7%A1%D7%B7%A2%D3%B7%A1%D1%E2%B7%A1%D7%D7%FC%B7%A0%A2%F7%E1%E6%F7%B7%A0%A2%E2%E0%FD%F0%FE%F7%FF%F3%B7%A0%A2%F3%E2%F3%E0%F7%F1%F7%FC%B7%A0%A2%D2%D2%E6%E0%F7%E1%D2%D2%B7%A0%A2%FF%F3%F5%FC%FB%E6%E7%F6%F7%E1%B7%A0%D1%B7%A0%A2%E2%FD%E0%B7%A0%A2%FE%FD%B7%A0%A2%E6%F3%FC%E6%FD%B7%A0%A2%F7%E1%E6%F3%FF%FD%E1%B7%A0%A2%F3%FC%E6%F7%B7%A0%A2%E7%FC%B7%A0%A2%E2%E0%FD%F0%FE%F7%FF%F3%B7%A0%A2%F6%F7%B7%A0%A2%E2%E0%FD%E2%FD%E0%F1%FB%FD%FC%F3%FE%FB%F6%F3%F6%B7%A0%A2%D2%D2%F1%FD%FF%E2%E7%F7%E1%E6%F3%D2%D2%BC%B7%A1%D1%BD%E2%B7%A1%D7%B7%A2%D3%B7%A1%D1%E2%B7%A1%D7%C1%FB%B7%A0%A2%E3%E7%F7%E0%F7%FF%FD%E1%B7%A0%A2%E1%F3%F0%F7%E0%B7%A0%A2%F1%E7%B7%D7%A3%FC%E6%FD%E1%B7%A0%A2%E6%E0%FD%E8%FD%E1%B7%A0%A2%F6%F7%B7%A0%A2%E6%F7%FE%F3%B7%A0%A2%F1%FD%FC%E1%F7%F5%E7%FB%E0%B7%D7%A3%B7%A0%A2%E7%FC%B7%A0%A2%F7%E3%E7%FB%E2%FD%B7%A0%A2%F6%F7%B7%A0%A2%A4%B7%A0%A2%E2%F7%E0%E1%FD%FC%F3%E1%B7%A0%A2%F7%FC%B7%A0%A2%A3%B7%A0%A2%F6%B7%D7%D6%F3%B7%A0%D1%B7%A0%A2%B7%D3%A3%F7%E1%B7%A0%A2%FF%E7%EB%B7%A0%A2%F4%B7%D7%A3%F1%FB%FE%B7%A0%A3%B7%A0%A2%E1%FD%FE%FD%B7%A0%A2%F6%F7%F0%F7%FF%FD%E1%B7%A0%A2%E7%E6%FB%FE%FB%E8%F3%E0%B7%A0%A2%FE%F3%B7%A0%A2%E0%F7%F5%FE%F3%B7%A0%A2%F6%F7%B7%A0%A2%E2%E0%FD%E2%FD%E0%F1%FB%FD%FC%F3%FE%FB%F6%F3%F6%B7%A0%A2%F1%FD%FF%E2%E7%F7%E1%E6%F3%B7%A0%D1%B7%A0%A2%EB%B7%A0%A2%F7%FE%B7%A0%A2%E0%F7%E1%E7%FE%E6%F3%F6%FD%B7%A0%A2%E1%F7%E0%B7%D7%A3%B7%A0%A2%F6%F7%B7%A0%A2%D2%D2%A3%A2%D2%D2%B7%A0%A2%E6%E0%FD%E8%FD%E1%BC%B7%A1%D1%BD%E2%B7%A1%D7%B7%A2%D3%B7%A1%D1%E2%B7%A1%D7%D3%F6%F7%FF%B7%D7%A3%E1%B7%A0%D1%B7%A0%A2%E1%FB%B7%A0%A2%E3%E7%F7%E0%F7%FF%FD%E1%B7%A0%A2%E1%F3%F0%F7%E0%B7%A0%A2%F1%E7%B7%D7%A3%FC%E6%FD%E1%B7%A0%A2%FF%FB%F7%FF%F0%E0%FD%E1%B7%A0%A2%F6%F7%F0%F7%E0%B7%D7%A3%B7%A0%A2%E6%F7%FC%F7%E0%B7%A0%A2%E7%FC%B7%A0%A2%F7%E3%E7%FB%E2%FD%B7%A0%A2%E2%F3%E0%F3%B7%A0%A2%F7%FC%F1%FD%FC%E6%E0%F3%E0%B7%A0%A2%A1%A2%B7%A0%A2%E6%E0%FD%E8%FD%E1%B7%A0%A2%F6%F7%B7%A0%A2%E6%F7%FE%F3%B7%A0%A2%F7%FC%B7%A0%A2%A0%B7%A0%A2%F6%B7%D7%D6%F3%E1%B7%A0%D1%B7%A0%A2%F6%F7%B7%A0%A2%FC%E7%F7%E4%FD%B7%A0%A2%E1%FD%FE%FD%B7%A0%A2%F6%F7%F0%F7%FF%FD%E1%B7%A0%A2%E7%E6%FB%FE%FB%E8%F3%E0%B7%A0%A2%FE%F3%B7%A0%A2%E0%F7%F5%FE%F3%B7%A0%A2%F6%F7%B7%A0%A2%E2%E0%FD%E2%FD%E0%F1%FB%FD%FC%F3%FE%FB%F6%F3%F6%B7%A0%A2%F1%FD%FF%E2%E7%F7%E1%E6%F3%B7%A0%D1%B7%A0%A2%EB%B7%A0%A2%F7%FE%B7%A0%A2%E0%F7%E1%E7%FE%E6%F3%F6%FD%B7%A0%A2%E1%F7%E0%B7%D7%A3%B7%A0%A2%F6%F7%B7%A0%A2%D2%D2%AB%D2%D2%B7%A0%A2%E2%F7%E0%E1%FD%FC%F3%E1%BC%B7%A1%D1%BD%E2%B7%A1%D7%B0%BE%B0%E1%FA%FD%E5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%FB%E6%FB%FC%F7%E0%F3%E0%EB%B0%A8%E9%B0%E1%FA%FD%E5%D1%FE%E7%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FE%E7%F7%D5%F3%FF%F7%B0%A8%B0%B0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F5%F7%D1%FE%E7%F7%B0%A8%A6%A2%BE%B0%E1%FA%FD%E5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%BE%B0%FF%F7%E1%E1%F3%F5%F7%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%EF%BE%B0%F1%F3%E1%F7%C1%F7%FC%E1%FB%E6%FB%E4%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%FB%E1%C1%F1%FD%E0%FF%B0%A8%A3%BE%B0%E6%F7%EA%E6%D0%E7%E6%E6%FD%FC%C1%F1%FD%E0%FF%B0%A8%B0%D5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%E0%F7%E2%F7%F3%E6%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%F4%F3%FE%E1%F7%BE%B0%E6%F7%EA%E6%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%B0%BE%B0%E6%F7%EA%E6%D3%F4%E6%F7%E0%B0%A8%B0%B0%BE%B0%F4%F7%F7%F6%D0%F3%F1%F9%B0%A8%F4%F3%FE%E1%F7%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F8%F7%D4%D0%B0%A8%A3%A2%A2%BE%B0%E4%F7%E0%E1%FB%FD%FC%B0%A8%A3%BE%B0%F7%E1%E6%E0%FB%F1%E6%D1%FA%F7%F1%F9%B0%A8%F4%F3%FE%E1%F7%BE%B0%E5%FD%E0%F6%E1%C1%FB%E8%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%E6%FB%FF%F7%B0%A8%A2%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%E5%FD%E0%F6%E1%D7%E0%E0%FD%E0%E1%B0%A8%B0%B0%BE%B0%F3%E6%E6%F7%FF%E2%E1%DC%E7%FF%F0%F7%E0%B0%A8%A3%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F8%F7%D7%E0%E0%FD%E0%B0%A8%A0%A2%BE%B0%E1%FA%FD%E5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%F4%F3%FE%E1%F7%BE%B0%E5%FD%E0%F6%E1%DE%FB%FF%FB%E6%B0%A8%F4%F3%FE%E1%F7%BE%B0%F7%E4%F3%FE%E7%F3%E6%FB%FD%FC%B0%A8%F4%F3%FE%E1%F7%BE%B0%F7%E4%F3%FE%E7%F3%E6%FB%FD%FC%DB%D6%B0%A8%B0%B0%BE%B0%FB%F6%B0%A8%B0%A0%A2%A0%A7%A3%A6%A3%A2%A6%A0%AA%BF%A4%A2%B0%BE%B0%FF%E1%F5%E1%B0%A8%E9%B0%FF%E1%F5%DA%F3%E2%E2%F7%FC%B0%A8%B0%C2%F3%E1%F3%E0%B0%BE%B0%FF%E1%F5%C0%F7%E2%FE%EB%B0%A8%B0%C0%F7%E1%E2%FD%FC%F6%F7%E0%B0%BE%B0%FF%E1%F5%C1%E7%F0%FF%FB%E6%B0%A8%B0%D7%FC%E4%FB%F3%E0%B0%BE%B0%FF%E1%F5%D7%FC%E6%F7%E0%D1%FD%F6%F7%B0%A8%B0%DB%FC%E6%E0%FD%F6%E7%F1%F7%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%D1%FD%F6%F7%B0%A8%B0%D7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B2%FC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B0%BE%B0%FF%E1%F5%D5%F3%FF%F7%DD%E4%F7%E0%B0%A8%B03%D4%FB%FC%B2%F6%F7%B2%FE%F3%B2%E2%F3%E0%E6%FB%F6%F3%B3%B0%BE%B0%FF%E1%F5%DB%FC%F6%FB%F1%F3%E6%F7%C5%FD%E0%F6%B0%A8%B0%C2%E0%FD%E2%FD%E0%F1%FB%FD%FC%F3%B2%E7%FC%F3%B2%E2%F3%FE%F3%F0%E0%F3%B2%FD%B2%F7%EA%E2%E0%F7%E1%FBa%FC%B0%BE%B0%FF%E1%F5%D1%FE%E7%F7%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B2%DE%F3%B2%E2%FB%E1%E6%F3%B2%F7%E1%A8%B0%BE%B0%FF%E1%F5%CB%FD%E7%DA%F3%E1%B0%A8%B0%C6%FB%F7%FC%F7%E1%B2%B7%A3%B2%F3%F1%FB%F7%E0%E6%FD%E1%B2%EB%B2%B7%A0%B2%F4%F3%FE%FE%FD%E1%B0%BE%B0%FF%E1%F5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%D1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%D3%F5%F3%FB%FC%B0%A8%B0%D8%E7%F5%F3%E0%B2%FD%E6%E0%F3%B2%E4%F7%E8%B0%BE%B0%FF%E1%F5%C0%F7%E3%E7%FB%E0%F7%F6%D3%F1%F1%F7%E1%E1%D9%F7%EB%B0%A8%B0%D7%E1%B2%FC%F7%F1%F7%E1%F3%E0%FB%FD%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%DE%FD%FD%F9%FB%FC%F5%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B2%DE%F3%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B2%E3%E7%F7%B2%F7%E1%E6%F3%F0%F3%E1%B2%F0%E7%E1%F1%F3%FC%F6%FD%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%E6%F3%E0%E6%B0%A8%B0%C2%E7%FE%E1%F3%B2%F3%E3%E7%7F%B2%E2%F3%E0%F3%B2%F8%E7%F5%F3%E0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%E1%B0%A8%B0%D7%E0%E0%FD%E0%F7%E1%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%B0%A8%B0%D7%E0%E0%FD%E0%B0%BE%B0%FF%E1%F5%DF%FD%E4%F7%DD%FC%F7%B0%A8%B0%C2%F3%E1%F3%E0%B0%BE%B0%FF%E1%F5%DA%FB%E6%E1%B0%A8%B0%D3%F1%FB%F7%E0%E6%FD%E1%B0%BE%B0%FF%E1%F5%DA%FB%E6%B0%A8%B0%D3%F1%FB%F7%E0%E6%FD%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%B0%DF%FB%FC%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%DF%F3%EA%FB%FF%FB%E8%F7%B0%A8%B0%DF%F3%EA%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%C6%FB%FF%F7%B0%A8%B0%DE%7F%FF%FB%E6%F7%B2%F6%F7%B2%E6%FB%F7%FF%E2%FD%B2%BA%FF%FF%A8%E1%E1%BB%B0%BE%B0%FF%E1%F5%DE%FB%E4%F7%B0%A8%B0%C4%FB%F6%F3%B0%BE%B0%FF%E1%F5%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C2%F3%FC%E6%F3%FE%FE%F3%B2%D1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%D7%EA%FB%E6%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C1%F3%FE%FB%E0%B2%F6%F7%FE%B2%FF%FD%F6%FD%B2%E2%F3%FC%E6%F3%FE%FE%F3%B2%F1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%DC%E7%FF%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%B0%DCh%FF%F7%E0%FD%B2%F6%F7%B2%E2%E0%F7%F5%E7%FC%E6%F3%E1%B0%BE%B0%FF%E1%F5%DC%FD%DB%FF%F3%F5%F7%B0%A8%B0%C2%E0%F7%F5%E7%FC%E6%F3%B2%E1%FB%FC%B2%FB%FFs%F5%F7%FC%F7%E1%B0%BE%B0%FF%E1%F5%D1%FD%FD%FE%B0%A8%B03%D0%FB%F7%FC%B3%B0%BE%B0%FF%E1%F5%DE%FD%E1%F7%C6%B0%A8%B0%DA%F3%E1%B2%E2%F7%E0%F6%FB%F6%FD%B2%A1%A1%A2%B2%E2%E7%FC%E6%FD%E1%B0%BE%B0%FF%E1%F5%DE%FD%E1%F7%DE%FB%E4%F7%B0%A8%B0%DA%F3%E1%B2%E2%F7%E0%F6%FB%F6%FD%B2%E7%FC%F3%B2%E4%FB%F6%F3%B0%BE%B0%FF%E1%F5%DE%FD%E1%E6%DE%FB%E4%F7%E1%B0%A8%B03%DA%F3%E1%B2%E2%F7%E0%F6%FB%F6%FD%B2%E6%FD%F6%F3%E1%B2%E1%E7%E1%B2%E4%FB%F6%F3%E1%B3%B0%BE%B0%FF%F5%E1%D3%FE%FE%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%B03%D1%FD%FF%E2%FE%F7%E6%F3%F6%F3%E1%B2%FE%F3%E1%B2%E2%E0%F7%F5%E7%FC%E6%F3%E1%B3%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F7%E1%B0%A8%B03%D1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%D7%EA%F1%F7%FE%F7%FC%E6%F7%B3%B2%EE%B23%D5%F7%FC%FB%F3%FE%B3%B2%EE%B23%DF%E7%EB%B2%F0%FB%F7%FC%B3%B2%EE%B23%C2%F7%E0%F4%F7%F1%E6%FD%B3%B0%BE%B0%FF%E1%F5%D4%F3%FB%FE%E7%E0%F7%E1%B0%A8%B03%DC%FD%B2%F7%E0%F3%B2%F7%E1%FD%B3%B2%EE%B23%DB%FC%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DE%FD%B2%E1%F7%FC%E6%FB%FF%FD%E1%B3%B2%EE%B23%D7%E0%E0%FD%E0%B3%B0%BE%B0%FF%E1%F5%C6%E0%EB%D3%F5%F3%FB%FC%B0%A8%B0%DC%F7%F1%F7%E1%FB%E6%F3%E1%B2%F3%FE%B2%FF%F7%FC%FD%E1%B2%E7%FC%B2%B7%E1%B7%B2%F6%F7%B2%E0%F7%E1%E2%E7%F7%E1%E6%F3%E1%B2%F1%FD%E0%E0%F7%F1%E6%F3%E1%B2%E2%F3%E0%F3%B2%F1%FD%FC%E1%F7%F5%E7%FB%E0%B2%FE%F3%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%BC%B2%C4%E7%F7%FE%E4%F7%B2%F3%B2%FB%FC%E6%F7%FC%E6%F3%E0%FE%FD%BC%B0%BE%B0%FF%E1%F5%C5%E0%FD%E6%F7%B0%A8%B0%D7%E1%F1%E0%FB%F0%F7%B2%FE%F3%B2%E2%F3%FE%F3%F0%E0%F3%B2%F1%FD%E0%E0%F7%F1%E6%F3%B2%EB%B2%E2%E7%FE%E1%F3%B2%F7%FC%B2%C0%F7%E1%E2%FD%FC%F6%F7%E0%BC%B2%C1%FB%B2%F6%E7%F6%F3%E1%BE%B2%E2%E7%FE%E1%F3%B2%F7%FC%B2%C1%F7%F5%E7%FB%E0%BC%B0%BE%B0%FF%E1%F5%DC%FD%E6%DC%F7%E6%E5%FD%E0%F9%B0%A8%B0%D3%B2%F7%E1%E6%F7%B2%F8%E7%F7%F5%FD%B2%E1a%FE%FD%B2%E1%F7%B2%E2%E7%F7%F6%F7%B2%F8%E7%F5%F3%E0%B2%F1%FD%FC%B2%F1%FD%FC%F7%EA%FBa%FC%B2%F3%B2%FB%FC%E6%F7%E0%FC%F7%E6%BC%B0%BE%B0%FF%E1%F5%D7%FC%F6%D5%F3%FF%F7%C1%F1%FD%E0%F7%B0%A8%B0%D3%FC%E6%F7%E1%B2%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F1%FD%FF%FB%F7%FC%E8%F3%B2%FE%F3%B2%E2%F3%E0%E6%FB%F6%F3%BC%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%C1%F1%FD%E0%FF%B0%A8%B0%DE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%FC%FD%B2%E1%F7%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%E2%FD%E0%E3%E7%F7%B2%F7%E1%E6%F3%B2%E2s%F5%FB%FC%F3%B2%FC%FD%B2%F4%FD%E0%FF%F3%B2%E2%F3%E0%E6%F7%B2%B2%F6%F7%B2%E7%FC%B2%E2%F3%E3%E7%F7%E6%F7%B2%C1%D1%DD%C0%DF%BC%B0%BE%B0%FF%E1%F5%C3%E7%F7%E1%E6%FB%FD%FC%B0%A8%B0%C2%E0%F7%F5%E7%FC%E6%F3%B0%BE%B0%FF%E1%F5%D3%FC%E1%E5%F7%E0%B0%A8%B0%C0%F7%E1%E2%FD%FC%F6%F7%E0%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%C1%F1%FD%E0%F7%B0%A8%B03%C1a%FE%FD%B2%E2%E7%F7%F6%F7%E1%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E7%FC%F3%B2%E4%F7%E8%B3%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%B0%A8%B0%C1a%FE%FD%B2%E2%E7%F7%F6%F7%E1%B2%F5%E7%F3%E0%F6%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%B0%BE%B0%FF%E1%F5%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%B0%A8%B0%DB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%CB%FD%E7%C1%F1%FD%E0%F7%B0%A8%B0%C6%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%D3%E7%E6%FA%FD%E0%B0%A8%B0%D3%E7%E6%FD%E0%7F%F3%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C6%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%BC%B2%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F8%E7%F5%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%BC%B0%BE%B0%FF%E1%F5%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C6%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F3%E7%E6%FD%FFs%E6%FB%F1%F3%FF%F7%FC%E6%F7%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%BC%B0%BE%B0%FF%E1%F5%C1%F7%E4%F7%E0%F3%FE%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%F7%F6%F7%E1%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E6%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%F1%FD%FF%FD%B2%E3%E7%FB%F7%E0%F3%E1%B0%BE%B0%FF%E1%F5%CB%FD%E7%DE%F3%E1%E6%C1%F1%FD%E0%F7%B0%A8%B0%DE%F3%B2h%FE%E6%FB%FF%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F5%E7%F3%E0%F6%F3%F6%F3%B2%F7%E1%B0%BE%B0%FF%E1%F5%D3%F1%E6%FB%E6%EB%D1%FD%FF%E2%FE%EB%B0%A8%B0%CB%F3%B2%FA%F3%E1%B2%E0%F7%F3%FE%FB%E8%F3%F6%FD%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%BC%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%F7%E4%F7%E0%F3%FE%C6%FB%FF%F7%E1%B0%A8%B0%C2%E7%F7%F6%F7%E1%B2%E0%F7%F3%FE%FB%E8%F3%E0%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%B2%F1%E7%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%E3%E7%FB%F7%E0%F3%E1%B0%BE%B0%FF%E1%F5%D1%FE%FD%E1%F7%B0%A8%B0%D1%F7%E0%E0%F3%E0%B0%BE%B0%FF%E1%F5%DE%FD%F3%F6%FB%FC%F5%B0%A8%B0%D1%F3%E0%F5%F3%FC%F6%FD%BC%B2%D7%E1%E2%F7%E0%F3%BE%B2%E2%FD%E0%B2%F4%F3%E4%FD%E0%BC%BC%BC%B0%BE%B0%FF%E1%F5%C2%FD%FB%FC%E6%E1%B0%A8%B0%E2%E7%FC%E6%FD%E1%B0%BE%B0%FF%E1%F5%D3%E7%F6%FB%FD%B0%A8%B0%D3%E7%F6%FB%FD%B0%BE%B0%FF%E1%F5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%B0%C1%FD%FE%E7%F1%FBa%FC%B0%BE%B0%FF%E1%F5%C6%E0%EB%B0%A8%B03%C2%E0%E7%F7%F0%F3%B2%FD%E6%E0%F3%B2%E4%F7%E8%B3%B0%BE%B0%FF%E1%F5%D1%FA%F7%F1%F9%B0%A8%B0%D1%FD%FF%E2%E0%FD%F0%F3%E0%B0%BE%B0%FF%E1%F5%D7%FC%F6%C1%F1%FD%E0%F7%B0%A8%B0%DA%F3%E1%B2%E6%F7%FC%FB%F6%FD%B2%B7%E1%B2%F3%F1%FB%F7%E0%E6%FD%E1%B2%EB%B2%B7%F6%B2%F7%E0%E0%FD%E0%F7%E1%BC%B0%BE%B0%FF%E1%F5%D7%FC%F6%C6%FB%FF%F7%B0%A8%B0%D7%FE%B2%E6%FB%F7%FF%E2%FD%B2%FA%F3%B2%F4%FB%FC%F3%FE%FB%E8%F3%F6%FD%BC%B0%BE%B0%FF%E1%F5%D5%F3%FF%F7%D7%FC%F6%B0%A8%B0%DA%F3%E1%B2%F1%FD%FF%E2%FE%F7%E6%F3%F6%FD%B2%FE%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%B0%BE%B0%FF%E1%F5%C7%FC%F1%FD%FF%E2%FE%F7%E6%F7%F6%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%FC%FD%B2%F1%FD%FF%E2%FE%F7%E6%F3%F6%F3%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F4%E7%FE%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%E1%E7%E2%F7%E0%F3%F6%F3%BC%B2%C2%E7%FC%E6%E7%F3%F1%FBa%FC%A8%B2%B7%E1%B0%BE%B0%FF%E1%F5%C7%FC%E1%E7%F1%F1%F7%E1%E1%F4%E7%FE%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%FC%FD%B2%E1%E7%E2%F7%E0%F3%F6%F3%BC%B2%C2%E7%FC%E6%E7%F3%F1%FBa%FC%A8%B2%B7%E1%B0%BE%B0%FF%E1%F5%C6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%D1%FD%FF%E2%FE%F7%E6%F3%B0%EF%EF

Tu equipo ya se ha puesto manos a la obra para crear la bolsa. Para conseguir y preparar 20 trozos de tela reciclados habéis necesitado 3 días de búsqueda y trabajo.

Vuestro equipo está formado por cuatro personas, la relación de proporcionalidad entre el número de integrantes del equipo y los trozos de tela conseguidos en 3 días es @@directamente@@ proporcional. Sin embargo, el número de personas que forman el equipo y los días que se han tardado en conseguir 20 trozos son @@inversamente@@ proporcionales.

En este problema aparecen @@tres@@ magnitudes, por lo tanto estamos ante un problema de proporcionalidad @@compuesta@@.

Si queremos saber cuántos trozos de tela conseguirá un equipo de 6 personas en 1 día, ¡es muy fácil! solo debemos utilizar la regla de proporcionalidad compuesta, y el resultado será de @@10@@ trozos.

Además, si queremos saber cuántos miembros deberá tener un equipo para encontrar 30 trozos de tela en 2 días, de nuevo solo debemos utilizar la regla de proporcionalidad compuesta, y el resultado será de @@9@@ personas.

Su navegador no es compatible con esta herramienta.

Un equilibrio precario

Crisis

La empresa de moda rápida Telimán está en crisis.

La causa es la competencia de marcas más sostenibles que ofrecen prendas de mayor calidad.

Telimán necesita cumplir con los siguientes objetivos:

Una creciente demanda de productos debido a la apertura de tiendas en Galicia.
Un acuerdo sindical para mejorar las condiciones laborales.
Un compromiso con el desarrollo sostenible.
La necesidad de reducir costes.

¿Puedes ayudar a esta empresa a lograr alguna de sus metas?

Elige una de esas opciones:

Lectura facilitada

Una empresa de moda rápida con sede en Asia:

Emplea a 500 trabajadores.
Busca aumentar sus ingresos en un 10% el próximo año.
En este año consiguió facturar 54 millones de euros.

Sin embargo, debe cumplir con el acuerdo laboral firmado con los sindicatos que implica:

Un aumento salarial del 1%.
Una reducción de la jornada laboral en una hora.

Actualmente el salario medio de la empresa de 250 € mensuales y las jornadas laborales de 10 horas al día.

¿Cómo puede esta empresa aumentar su producción, mejorar su cadena de suministro o incrementar el precio de venta para alcanzar sus objetivos?

Opción A. Expansión gallega

Los datos

Pictograma ingreso

Para fijar los precios de la ropa en las nuevas tiendas de Galicia, es importante analizar los siguientes datos sobre la empresa:

Se pusieron 16 millones de prendas a la venta el año pasado,
Las prendas se vendieron en un total de 80 tiendas.
Se facturaron 200 millones de euros el último año.

Para resolver los problemas planteados, supondremos que estas tres magnitudes son directamente proporcionales.

Las previsiones

Pictograma centro de datos

Teniendo en cuenta los datos anteriores y suponiendo que todas las ventas tienen el mismo rendimiento:

¿Cuántas prendas vendió cada tienda?
¿Cuánto tardarían en vender la misma cantidad de prendas si abriesen 10 tiendas más?

Tiendas gallegas

Pictograma sostenible

La empresa tiene que decidir cuántas tiendas van a abrir en Galicia:

¿Cuántas tiendas deberían abrirse si se pretende facturar un 10 % más?
¿Cuántas prendas estimas que se venderán en estas tiendas?
¿Cuánto facturarán estas tiendas si su rendimiento es similar al del resto de tiendas?

¿Cuáles son las magnitudes?

En estos ejercicios intervienen varias magnitudes,

N.º de prendas
N.º de tiendas
Facturación (millones de €)
Tiempo (años)

Forma dos tablas con tres columnas cada una donde indiques las tres magnitudes que intervienen en cada apartado con los datos correspondientes.

Opción B. Acuerdo sindical

Las condiciones

Pictograma justicia social El actual salario en esta empresa es de 270 € mensuales.

Las jornadas laborales son de 10 horas al día.

En el acuerdo firmado con los sindicatos se compromete a:

Aumentar el salario el 1 %.
Reducir la jornada laboral 1 hora.

Un antes y un después

Pictograma dinero El actual salario en esta empresa es de 270 € mensuales.

Con la información dada, calcula

¿Cuánto pagaba por hora esta empresa antes del acuerdo?
¿Cuánto pagaba por hora esta empresa después del acuerdo?

Personas contratadas

Pictograma empresaria El actual salario en esta empresa es de 270 € mensuales.

Si la empresa tiene a 500 personas contratadas,

¿Cuánto dinero anual se destinaba a los salarios antes del acuerdo?
¿Cuánto dinero anual se destina a los salarios tras el acuerdo?

La producción

Pictograma camiseta El actual salario en esta empresa es de 270 € mensuales.

La fábrica producía 2000 camisetas en las condiciones anteriores al acuerdo.

Con la reducción de jornada acordada, ¿cuántas personas tendrá que contratar a mayores para seguir produciendo el mismo número de camisetas?

¿Cuáles son las magnitudes?

En estos problemas interviene varias magnitudes,

Sueldo (€)
Tiempo de la jornada (horas)
N.º días
N.º trabajadores
N.º camisetas

Para cada pregunta, forma una tabla con tres columnas donde indiques las tres magnitudes que intervienen.

Una vez identificadas las magnitudes, recuerda analizar si las proporcionalidades son directas o inversas.

Opción C. Desarrollo sostenible

Objetivo

Pictograma sostenible

El desarrollo sostenible de la empresa es cada vez más necesario.

No solo por las leyes internacionales impulsadas por la OIT que lo exigen, sino también porque el mercado así lo demanda.

El objetivo de la empresa es aumentar su producción un 10 % para poder abastecer las nuevas tiendas de ropa que han abierto en Galicia.

Analiza estas dos propuestas.

1. Personal

Pictograma empresaria

Contratar a más personal permitiría aumentar la capacidad productiva y darle la oportunidad a las personas contratadas de conciliar su vida laboral con su vida familiar.

La contratación de 10 nuevos trabajadores supone un aumento medio de la producción del 2 %.
La inversión en formación supone unos 50 € por empleado/a.

Análisis 1

Analiza la segunda estrategia y contesta razonadamente:

¿Cuántas personas deberían contratar para conseguir su objetivo?
¿Cuánto gastaría la empresa en formación de estas personas?

2. Producción

Pictograma tienda de costura

Implementar nuevas tecnologías aumentaría la eficiencia del proceso, mejorando las condiciones del personal que trabaja con las máquinas, optimizando los recursos y contaminando menos.

Actualmente, las 1000 máquinas de coser de la fábrica están obsoletas.
La renovación de 50 máquinas supondría un coste de 600 €,
Cada 10 máquinas adquiridas aumentaría la producción un 0,1 %.

Análisis 2

Analiza la primera estrategia y contesta razonadamente:

¿Cuántas máquinas debería renovar para conseguir su objetivo?
¿Cuál sería la inversión de la empresa?

Compara

Pictograma selección

Has analizado las dos estrategias anteriores.

¿Cuál de las dos opciones recomendarías para alcanzar el objetivo? Razona la respuesta.

La fábrica producía 2000 camisetas al día con una jornada continua de 9 horas al día.

Si en ambos casos se mejora la producción un 10 %,

¿cuántas camisetas fabricarán en 9 horas?
¿cuántas horas tardarán en fabricar el mismo número de camisetas? Indica el resultado aproximando en horas y minutos.

¿Cuáles son las magnitudes?

En la primera estrategia intervienen tres magnitudes,

N.º máquinas
Inversión (€)
Mejora producción (%)

En la segunda estrategia intervienen tres magnitudes,

N.º trabajadores
Inversión inicial (€)
Mejora producción (%)

En el análisis final intervienen tres magnitudes,

N.º camisetas
Producción (%)
Tiempo (h)

Forma tres tablas con tres columnas cada una donde indiques las tres magnitudes con los datos correspondientes.

Opción D. Reducir costes

Datos

La empresa Telimán se propone reducir gastos para invertir en la apertura de tiendas en Galicia, quiere respetar el acuerdo sindical y, además, mantener su compromiso con el desarrollo sostenible. Los datos que analizan son los siguientes:

Se facturan aproximadamente 200 millones de euros año.
El año pasado, el 60 % de la facturación de la empresa fue destinado a pagar los costes de producción.
La distribución de los costes de producción se divide en:

Coste de materias primas	35 %
Coste de transporte	15 %
Coste de almacenamiento	5 %
Coste de la mano de obra	45 %

Antes de tomar ninguna decisión, las personas que dirigen la empresa recuerdan que:

Para respetar el acuerdo sindical, el salario de las personas que trabajan en sus fábricas ha incrementado los gastos en mano de obra en un 1 %.
Para mejorar la calidad de sus prendas y mantener su compromiso con el desarrollo sostenible, han aumentado los costes de materias primas en un 5 %.

Por lo tanto, solo les quedarían dos opciones si quieren reducir gastos: reducir costes de almacenamiento o de transporte.

Análisis

Con los datos anteriores, razona y calcula,

El año pasado, ¿cuánto dinero se destinó a cada uno de los cuatro apartados de la tabla? Pista: calcula en millones de €.
Aumentando los gastos en materia prima y mano de obra, ¿cuánto dinero se destinará a cada uno de los cuatro apartados?
Haz una tabla indicando los nuevos porcentajes de costes de producción. Pista: recuerda que la suma debe dar 100 %.
¿Sabrías calcular los porcentajes anteriores haciendo una única operación para cada uno de los costes?

1. Almacenamiento

La empresa tiene 4 fábricas, un almacén central y 80 tiendas en diferentes ciudades.

La empresa quiere reducir los gastos de almacenamiento evitando que se acumulen demasiadas prendas en el almacén.

Pictograma acordar

Deciden contratar a Carme Piñeiro, reputada gerente de logística e inventarios.

Carme comunica a la empresa que quiere contratar a su propio equipo de trabajo con las siguientes condiciones:

10 personas contratadas aumentan los gastos en personal un 0,1 %.
5 personas contratadas reducen el coste de almacenamiento un 0,25 %.

2. Transporte

Pictograma empresa de mensajería

Mejorar el proceso de entrega de los productos a las tiendas puede reducir significativamente los costes de transporte y almacenamiento. Una planificación cuidadosa de las rutas y la adquisición de vehículos más sostenibles permitirán entregar los productos de manera más rápida y económica.

La inversión de 20 nuevas furgonetas por 30 000 € cada una, implicaría una reducción del 10 % del coste de transporte.
La compra de un software para planificar las rutas tiene un precio de 200 € al año e implicaría la reducción del coste de transporte del 1 %.

Compara

Pictograma selección

Compara y contesta razonadamente:

Si se contratan 20 personas para el almacén, ¿cuál sería el ahorro total en costes de almacenamiento? ¿Cuánto se gastaría en los nuevos trabajadores?
¿Cuál es el ahorro en costes de transporte si se invierte en las 20 nuevas furgonetas y el software? ¿Cuál debe ser la inversión inicial?
¿Cuál de las dos opciones (contratar personal o invertir en tecnología) generaría un mayor ahorro?
¿Cuál de las dos opciones crees que tendría un mayor impacto positivo en la sostenibilidad de la empresa?

Definiciones

Proporcionalidad compuesta

Cuando más de dos magnitudes tienen una relación de proporcionalidad hablamos de proporcionalidad compuesta.

Composición de tres en raya con letras. Para resolver estos problemas, debemos estudiar la proporcionalidad entre la magnitud principal y las demás magnitudes implicadas, pudiendo ser directa o inversa.

Además, debes tener en cuenta que:

- La relación de proporcionalidad directa no altera la razón de proporcionalidad.

- La relación de proporcionalidad inversa invierte la razón de proporcionalidad.

Por ejemplo:

En la siguiente tabla se muestra la relación de proporcionalidad de las magnitudes A y B con respecto a la magnitud C.

Relación de proporcionalidad entre tres magnitudes

A partir de esta tabla es posible obtener las razones de proporcionalidad de las magnitudes.

\(\dfrac{ a_1 }{a_2} \text{ , }\dfrac{ b_1 }{b_2} \text{ y }\dfrac{ c_1 }{x}\)

Entonces, puedes establecer la siguiente relación entre las razones de proporcionalidad de las tres magnitudes:

\(\dfrac{ c_1 }{x} = \dfrac{ a_2 }{a_1}· \dfrac{ b_1 }{b_2}\)

Finalmente, puedes obtener la cantidad a calcular:

\(x=\dfrac{ a_1 · b_2 · c_1}{a_2·b_1}\)

Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0