Glosario
Magnitud
-
Definición:
-
Característica que se puede medir.
-
Ejemplo:
-
La longitud de un pantalón es medible, generalmente se mide en centímetros.
ReMates y ReTales
2.1. Tallas proporcionales
Midiendo la industria de la moda
Como ya has visto, para crear una pieza de ropa entran en acción muchos aspectos diferentes. Además, el impacto de la industria de la moda en Galicia afecta de varias formas a nuestra comunidad, como en la cantidad de ganancias que aporta, el número de empleos, los recursos que consume...
¿Se puede medir ese impacto?
¿Recuerdas cómo se llamaban aquellas propiedades medibles?
Lectura facilitada
Para crear una pieza de ropa se usan aspectos diferentes.
El impacto de la industria de la moda en Galicia afecta de varias formas, como:
- cantidad de ganancias
- el número de empleos
- los recursos que consume...
¿Se puede medir ese impacto?
¿Recuerdas cómo se llamaban aquellas propiedades medibles?
Magnitudes
Una magnitud es una propiedad física que se puede medir.
La cantidad que se toma de una magnitud indica con las unidades de medida, que ya viste el curso pasado.
Están recogidas en el Sistema Internacional de Unidades. Cada una de ellas tiene múltiplos y submúltiplos.
Para matematizar problemas de la vida cotidiana, es importante:
- Identificar las magnitudes presentes en el problema.
- Definir el múltiplo o submúltiplo de la unidad más adecuado en cada una de ellas.
Indicaremos esta información de la forma siguiente:
Magnitud (unidades)
Hay conceptos que no son medibles como lo que nos favorece un pantalón o si este está a la moda. No son valores objetivos por lo que no son magnitudes.
Ejemplos
Ejemplos de magnitudes son:
- Las ganancias de la industria de la moda, que podemos medir en millones de euros. Lo indicaremos como: Ganancias (millones de €)
- El largo de un vaquero, en centímetros. Lo indicaremos como: Largo de un vaquero (cm)
Fíjate, cuando tenemos varias cantidades de una magnitud siempre hay que buscar el múltiplo o submúltiplo más adecuado para indicar su valor.
Por ejemplo:
No es lo mismo medir el peso de un botón que el peso de unas botas de trabajo.
Probablemente mediremos el primero en miligramos (mg) y el segundo en kilogramos (kg).
La unidad de medida del peso de ambos es el gramo, pero el botón se indica en el submúltiplo "mili" mientras que el de las botas se dará en el múltiplo "kilo".
Indicaremos esta información de la forma siguiente:
Peso de un botón (mg)
Peso de unas botas (kg)
El reto y sus magnitudes
Arrastra cada tarjeta al bloque que corresponda, magnitud o no magnitud. Repasa la definición de magnitud si necesitas ayuda.
%E9%B0%E6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%D1%FE%F3%E1%FB%F4%FB%F1%F3%B0%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%FB%FC%E1%E6%E0%E7%F1%E6%FB%FD%FC%E1%B0%A8%B0%AE%E2%AC%D3%E0%E0%F3%E1%E6%E0%F3%B2%F1%F3%F6%F3%B2%E6%F3%E0%F8%F7%E6%F3%B2%F3%FE%B2%F0%FE%FD%E3%E7%F7%B2%E3%E7%F7%B2%F1%FD%E0%E0%F7%E1%E2%FD%FC%F6%F3%BE%B2%FF%F3%F5%FC%FB%E6%E7%F6%B2%FD%B2%FC%FD%B2%FF%F3%F5%FC%FB%E6%E7%F6%BC%B2%C0%F7%E2%F3%E1%F3%B2%FE%F3%B2%F6%F7%F4%FB%FC%FB%F1%FBa%FC%B2%F6%F7%B2%FF%F3%F5%FC%FB%E6%E7%F6%B2%E1%FB%B2%FC%F7%F1%F7%E1%FB%E6%F3%E1%B2%F3%EB%E7%F6%F3%BC%AE%BD%E2%AC%B0%BE%B0%E1%FA%FD%E5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%FB%E6%FB%FC%F7%E0%F3%E0%EB%B0%A8%E9%B0%E1%FA%FD%E5%D1%FE%E7%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FE%E7%F7%D5%F3%FF%F7%B0%A8%B0%B0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F5%F7%D1%FE%E7%F7%B0%A8%A6%A2%BE%B0%E1%FA%FD%E5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%BE%B0%FF%F7%E1%E1%F3%F5%F7%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%EF%BE%B0%E5%FD%E0%F6%E1%D5%F3%FF%F7%B0%A8%C9%E9%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%F7%C6%F7%EA%E6%B0%A8%B0%D3%FC%F1%FA%E7%E0%F3%B2%F6%F7%B2%FE%F3%B2%F0%FD%FE%E1%F3%B0%BE%B0%F1%FD%FE%FD%E0%B0%A8%B0%B1%A2%AA%A2%AA%A2%AA%B0%BE%B0%F0%F3%F1%F9%F1%FD%FE%FD%E0%B0%A8%B0%B1%AB%F0%F6%AB%F1%F4%B0%BE%B0%F5%E0%FD%E7%E2%B0%A8%A2%BE%B0%FF%E1%F5%DA%FB%E6%B0%A8%B0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%F7%C6%F7%EA%E6%B0%A8%B0%D0%F7%FE%FE%F7%E8%F3%B2%F6%F7%B2%FE%F3%B2%F0%FD%FE%E1%F3%B0%BE%B0%F1%FD%FE%FD%E0%B0%A8%B0%B1%A2%A2%A2%A2%A2%A2%B0%BE%B0%F0%F3%F1%F9%F1%FD%FE%FD%E0%B0%A8%B0%B1%F4%A7%F4%AA%A4%A1%B0%BE%B0%F5%E0%FD%E7%E2%B0%A8%A3%BE%B0%FF%E1%F5%DA%FB%E6%B0%A8%B0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%F7%C6%F7%EA%E6%B0%A8%B0%D1%FD%E1%E6%F7%B2%F6%F7%B2%FE%FD%E1%B2%FF%F3%E6%F7%E0%FB%F3%FE%F7%E1%B0%BE%B0%F1%FD%FE%FD%E0%B0%A8%B0%B1%A2%A2%A2%A2%A2%A2%B0%BE%B0%F0%F3%F1%F9%F1%FD%FE%FD%E0%B0%A8%B0%B1%AA%A0%F7%F1%A5%A6%B0%BE%B0%F5%E0%FD%E7%E2%B0%A8%A2%BE%B0%FF%E1%F5%DA%FB%E6%B0%A8%B0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%F7%C6%F7%EA%E6%B0%A8%B0%C6%FB%F7%FF%E2%FD%B2%F6%F7%B2%E6%E0%F3%F0%F3%F8%FD%B0%BE%B0%F1%FD%FE%FD%E0%B0%A8%B0%B1%A2%A2%A2%A2%A2%A2%B0%BE%B0%F0%F3%F1%F9%F1%FD%FE%FD%E0%B0%A8%B0%B1%F4%A6%A5%A4%F7%AB%B0%BE%B0%F5%E0%FD%E7%E2%B0%A8%A2%BE%B0%FF%E1%F5%DA%FB%E6%B0%A8%B0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%F7%C6%F7%EA%E6%B0%A8%B0%C2%E0%F7%F1%FB%FD%B2%F6%F7%B2%E4%F7%FC%E6%F3%B0%BE%B0%F1%FD%FE%FD%E0%B0%A8%B0%B1%A2%A2%A2%A2%A2%A2%B0%BE%B0%F0%F3%F1%F9%F1%FD%FE%FD%E0%B0%A8%B0%B1%F7%A1%A4%A0%A7%AB%B0%BE%B0%F5%E0%FD%E7%E2%B0%A8%A2%BE%B0%FF%E1%F5%DA%FB%E6%B0%A8%B0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%B0%A8%B0%B0%EF%BE%E9%B0%E6%EB%E2%F7%B0%A8%A3%BE%B0%EA%B0%A8%A2%BE%B0%EB%B0%A8%A2%BE%B0%F3%E7%E6%FA%FD%E0%B0%A8%B0%B0%BE%B0%F3%FE%E6%B0%A8%B0%B0%BE%B0%E7%E0%FE%B0%A8%B0%B0%BE%B0%F3%E7%F6%FB%FD%B0%A8%B0%B0%BE%B0%F7%C6%F7%EA%E6%B0%A8%B0%C7%E6%FB%FE%FB%F6%F3%F6%B0%BE%B0%F1%FD%FE%FD%E0%B0%A8%B0%B1%A2%A2%A2%A2%A2%A2%B0%BE%B0%F0%F3%F1%F9%F1%FD%FE%FD%E0%B0%A8%B0%B1%F1%F1%AB%F4%F7%AB%B0%BE%B0%F5%E0%FD%E7%E2%B0%A8%A3%BE%B0%FF%E1%F5%DA%FB%E6%B0%A8%B0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%B0%A8%B0%B0%EF%CF%BE%B0%FB%E1%C1%F1%FD%E0%FF%B0%A8%A3%BE%B0%E6%F7%EA%E6%D0%E7%E6%E6%FD%FC%C1%F1%FD%E0%FF%B0%A8%B0%D5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%E0%F7%E2%F7%F3%E6%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%F4%F3%FE%E1%F7%BE%B0%E6%F7%EA%E6%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%B0%BE%B0%E6%F7%EA%E6%D3%F4%E6%F7%E0%B0%A8%B0%B0%BE%B0%F4%F7%F7%F6%D0%F3%F1%F9%B0%A8%F4%F3%FE%E1%F7%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F8%F7%D4%D0%B0%A8%A3%A2%A2%BE%B0%F1%E7%E1%E6%FD%FF%DF%F7%E1%E1%F3%F5%F7%E1%B0%A8%F4%F3%FE%E1%F7%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F8%F7%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%A3%A2%A2%BE%B0%E6%FB%FF%F7%B0%A8%A2%BE%B0%E4%F7%E0%E1%FB%FD%FC%B0%A8%A2%BC%AA%BE%B0%F5%E0%FD%E7%E2%E1%B0%A8%C9%B0%DF%F3%F5%FC%FB%E6%E7%F6%B0%BE%B0%DC%FD%B2%FF%F3%F5%FC%FB%E6%E7%F6%B0%BE%B0%D5%E0%E7%E2%FD%B2%A1%B0%BE%B0%D5%E0%E7%E2%FD%B2%A6%B0%CF%BE%B0%FC%E7%FF%F0%F7%E0%D5%E0%FD%E7%E2%E1%B0%A8%A0%BE%B0%F5%F3%FF%F7%DE%F7%E4%F7%FE%B0%A8%A0%BE%B0%F7%E4%F3%FE%E7%F3%E6%FB%FD%FC%B0%A8%F4%F3%FE%E1%F7%BE%B0%F7%E4%F3%FE%E7%F3%E6%FB%FD%FC%DB%D6%B0%A8%B0%B0%BE%B0%FB%F6%B0%A8%B0%A0%A2%A0%A6%A3%A0%A1%A3%A4%A0%A6%A3%A1%BF%A4%A2%B0%BE%B0%FF%E1%F5%E1%B0%A8%E9%B0%FF%E1%F5%C1%E7%F0%FF%FB%E6%B0%A8%B0%D7%FC%E4%FB%F3%E0%B0%BE%B0%FF%E1%F5%D1%FE%E7%F7%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B2%DE%F3%B2%E2%FB%E1%E6%F3%B2%F7%E1%A8%B0%BE%B0%FF%E1%F5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%D1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%D3%F5%F3%FB%FC%B0%A8%B0%D8%E7%F7%F5%F3%B2%FD%E6%E0%F3%B2%E4%F7%E8%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%E6%F3%E0%E6%B0%A8%B0%C2%E7%FE%E1%F3%B2%F3%E3%E7%7F%B2%E2%F3%E0%F3%B2%F8%E7%F5%F3%E0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%E1%B0%A8%B0%D7%E0%E0%FD%E0%F7%E1%B0%BE%B0%FF%E1%F5%DA%FB%E6%E1%B0%A8%B0%D3%F1%FB%F7%E0%E6%FD%E1%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%B0%DF%FB%FC%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%DF%F3%EA%FB%FF%FB%E8%F7%B0%A8%B0%DF%F3%EA%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C2%F3%FC%E6%F3%FE%FE%F3%B2%D1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%D7%EA%FB%E6%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C1%F3%FE%FB%E0%B2%F6%F7%FE%B2%FF%FD%F6%FD%B2%E2%F3%FC%E6%F3%FE%FE%F3%B2%F1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%DC%E7%FF%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%B0%DCh%FF%F7%E0%FD%B2%F6%F7%B2%E2%E0%F7%F5%E7%FC%E6%F3%E1%B0%BE%B0%FF%E1%F5%DC%FD%DB%FF%F3%F5%F7%B0%A8%B0%C2%E0%F7%F5%E7%FC%E6%F3%B2%E1%FB%FC%B2%FB%FFs%F5%F7%FC%F7%E1%B0%BE%B0%FF%E1%F5%D1%FD%FD%FE%B0%A8%B03%D0%FB%F7%FC%B3%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F7%E1%B0%A8%B03%D1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%D7%EA%F1%F7%FE%F7%FC%E6%F7%B3%B2%EE%B23%D5%F7%FC%FB%F3%FE%B3%B2%EE%B23%DF%E7%EB%B2%F0%FB%F7%FC%B3%B2%EE%B23%C2%F7%E0%F4%F7%F1%E6%FD%B3%B0%BE%B0%FF%E1%F5%D4%F3%FB%FE%E7%E0%F7%E1%B0%A8%B03%DC%FD%B2%F7%E0%F3%B2%F7%E1%FD%B3%B2%EE%B23%DB%FC%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DE%FD%B2%E1%F7%FC%E6%FB%FF%FD%E1%B3%B2%EE%B23%D7%E0%E0%FD%E0%B3%B0%BE%B0%FF%E1%F5%C6%E0%EB%D3%F5%F3%FB%FC%B0%A8%B0%DC%F7%F1%F7%E1%FB%E6%F3%E1%B2%F3%FE%B2%FF%F7%FC%FD%E1%B2%E7%FC%B2%B7%E1%B7%B2%F6%F7%B2%E0%F7%E1%E2%E7%F7%E1%E6%F3%E1%B2%F1%FD%E0%E0%F7%F1%E6%F3%E1%B2%E2%F3%E0%F3%B2%F1%FD%FC%E1%F7%F5%E7%FB%E0%B2%FE%F3%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%BC%B2%C4%E7%F7%FE%E4%F7%B2%F3%B2%FB%FC%E6%F7%FC%E6%F3%E0%FE%FD%BC%B0%BE%B0%FF%E1%F5%D7%FC%F6%D5%F3%FF%F7%C1%F1%FD%E0%F7%B0%A8%B0%D3%FC%E6%F7%E1%B2%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F1%FD%FF%FB%F7%FC%E8%F3%B2%FE%F3%B2%E2%F3%E0%E6%FB%F6%F3%BC%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%C1%F1%FD%E0%FF%B0%A8%B0%DE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%FC%FD%B2%E1%F7%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%E2%FD%E0%E3%E7%F7%B2%F7%E1%E6%F3%B2%E2s%F5%FB%FC%F3%B2%FC%FD%B2%F4%FD%E0%FF%F3%B2%E2%F3%E0%E6%F7%B2%B2%F6%F7%B2%E7%FC%B2%E2%F3%E3%E7%F7%E6%F7%B2%C1%D1%DD%C0%DF%BC%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%C1%F1%FD%E0%F7%B0%A8%B03%C1a%FE%FD%B2%E2%E7%F7%F6%F7%E1%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E7%FC%F3%B2%E4%F7%E8%B3%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%B0%A8%B0%C1a%FE%FD%B2%E2%E7%F7%F6%F7%E1%B2%F5%E7%F3%E0%F6%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%B0%BE%B0%FF%E1%F5%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%B0%A8%B0%DB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%CB%FD%E7%C1%F1%FD%E0%F7%B0%A8%B0%C6%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%D3%E7%E6%FA%FD%E0%B0%A8%B0%D3%E7%E6%FD%E0%7F%F3%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C6%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%BC%B2%C1a%FE%FD%B2%E2%E7%F7%F6%F7%E1%B2%F8%E7%F5%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%BC%B0%BE%B0%FF%E1%F5%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C6%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F3%E7%E6%FD%FFs%E6%FB%F1%F3%FF%F7%FC%E6%F7%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%BC%B0%BE%B0%FF%E1%F5%C1%F7%E4%F7%E0%F3%FE%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%F7%F6%F7%E1%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E6%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%F1%FD%FF%FD%B2%E3%E7%FB%F7%E0%F3%E1%B0%BE%B0%FF%E1%F5%CB%FD%E7%DE%F3%E1%E6%C1%F1%FD%E0%F7%B0%A8%B0%DE%F3%B2h%FE%E6%FB%FF%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F5%E7%F3%E0%F6%F3%F6%F3%B2%F7%E1%B0%BE%B0%FF%E1%F5%D3%F1%E6%FB%E6%EB%D1%FD%FF%E2%FE%EB%B0%A8%B0%CB%F3%B2%FA%F3%E1%B2%E0%F7%F3%FE%FB%E8%F3%F6%FD%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%BC%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%F7%E4%F7%E0%F3%FE%C6%FB%FF%F7%E1%B0%A8%B0%C2%E7%F7%F6%F7%E1%B2%E0%F7%F3%FE%FB%E8%F3%E0%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%B2%F1%E7%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%E3%E7%FB%F7%E0%F3%E1%BC%B0%BE%B0%FF%E1%F5%D1%FE%FD%E1%F7%B0%A8%B0%D1%F7%E0%E0%F3%E0%B0%BE%B0%FF%E1%F5%D3%E7%F6%FB%FD%B0%A8%B0%D3%E7%F6%FB%FD%B0%BE%B0%FF%E1%F5%CB%F7%E1%B0%A8%B0%C1%7F%B0%BE%B0%FF%E1%F5%DC%FD%B0%A8%B0%DC%FD%B0%BE%B0%FF%E1%F5%C6%FB%FF%F7%DD%E4%F7%E0%B0%A8%B0%C6%E7%B2%E6%FB%F7%FF%E2%FD%B2%FA%F3%B2%F4%FB%FC%F3%FE%FB%E8%F3%F6%FD%BC%B2%DB%FC%E6%7B%FC%E6%F3%FE%FD%B2%F6%F7%B2%FC%E7%F7%E4%FD%B0%BE%B0%FF%F5%E1%D5%F3%FF%F7%C1%E6%F3%E0%E6%B0%A8%B03%D7%FE%B2%F8%E7%F7%F5%FD%B2%FA%F3%B2%F1%FD%FF%F7%FC%E8%F3%F6%FD%B3%B2%D3%E0%E0%F3%E1%E6%E0%F3%B2%F1%F3%F6%F3%B2%E6%F3%E0%F8%F7%E6%F3%B2%FA%F3%E1%E6%F3%B2%E1%E7%B2%F1%FD%FC%E6%F7%FC%F7%F6%FD%E0%B0%BE%B0%FF%E1%F5%C1%F7%FE%F7%F1%E6%D1%F3%E0%F6%B0%A8%B0%C1%F7%FE%F7%F1%F1%FB%FD%FC%F3%B2%FD%E6%E0%F3%B2%E6%F3%E0%F8%F7%E6%F3%B0%BE%B0%FF%E1%F5%C1%F7%FE%F7%F1%E6%D1%F3%E0%F6%DD%FC%F7%B0%A8%B0%C1%F7%FE%F7%F1%F1%FB%FD%FC%F3%B2%E7%FC%F3%B2%E6%F3%E0%F8%F7%E6%F3%B0%BE%B0%FF%E1%F5%C0%F7%F0%FD%FD%E6%B0%A8%B0%C0%F7%FB%FC%FB%F1%FB%F3%E0%B0%BE%B0%FF%E1%F5%C6%F7%E1%E6%C2%F3%E1%E1%F7%F6%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B23%C2%E0%E7%F7%F0%F3%B2%E1%E7%E2%F7%E0%F3%F6%F3%B3%B0%BE%B0%FF%E1%F5%C6%F7%E1%E6%D4%F3%FB%FE%F7%F6%B0%A8%B0%DC%FD%B2%FA%F3%E1%B2%E1%E7%E2%F7%E0%F3%F6%FD%B2%FE%F3%B2%E2%E0%E7%F7%F0%F3%BC%B2%DB%FC%E6%7B%FC%E6%F3%FE%FD%B2%F6%F7%B2%FC%E7%F7%E4%FD%B0%BE%B0%FF%E1%F5%C0%F7%F0%FD%FD%E6%D5%F3%FF%F7%B0%A8%B0-%D6%F7%E1%F7%F3%E1%B2%E0%F7%FB%FC%FB%F1%FB%F3%E0%B2%F7%E1%E6%F3%B2%E2%F3%E0%E6%FB%F6%F3%AD%B0%BE%B0%FF%E1%F5%D1%FD%FC%E6%FB%FC%E7%F7%B0%A8%B0%D1%FD%FC%E6%FB%FC%E7%F3%E0%B0%BE%B0%FF%E1%F5%C1%FA%FD%E5%D3%FC%E1%E5%F7%E0%E1%B0%A8%B0%D1%FD%FF%E2%E0%FD%F0%F3%E0%B2%E0%F7%E1%E7%FE%E6%F3%F6%FD%E1%B0%BE%B0%FF%E1%F5%C7%FC%F3%FC%E1%E5%F7%E0%F7%F6%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%B0%C6%F7%B2%FA%F3%FC%B2%E3%E7%F7%F6%F3%F6%FD%B2%B7%E1%B2%E6%F3%E0%F8%F7%E6%F3%E1%B2%E2%FD%E0%B2%F1%FD%FE%FD%F1%F3%E0%B2%F1%FD%E0%E0%F7%F1%E6%F3%FF%F7%FC%E6%F7%BC%B2-%C3%E7%FB%F7%E0%F7%E1%B2%FB%FC%E6%F7%FC%E6%F3%E0%FE%FD%B2%F6%F7%B2%FC%E7%F7%E4%FD%AD%B0%BE%B0%FF%E1%F5%D3%FE%FE%D1%FD%E0%E0%F7%F1%E6%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B23%C6%FD%F6%FD%B2%E2%F7%E0%F4%F7%F1%E6%FD%B3%B0%BE%B0%FF%E1%F5%C6%FD%FD%DF%F3%FC%EB%C6%E0%FB%F7%E1%B0%A8%B03%D7%E1%E6%E7%E2%F7%FC%F6%FD%B3%B2%DA%F3%E1%B2%E0%F7%E1%E7%F7%FE%E6%FD%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%B2%F7%FC%B2%B7%E1%B2%FB%FC%E6%F7%FC%E6%FD%E1%BC%B23%C1%F7%F5%E7%E0%FD%B2%E3%E7%F7%B2%E2%E7%F7%F6%F7%E1%B2%FA%F3%F1%F7%E0%FE%FD%B2%FFs%E1%B2%E0s%E2%FB%F6%FD%B3%B0%BE%B0%FF%E1%F5%C3%A7%B0%A8%B0%DC%FD%B2%FA%F3%E1%B2%F1%FD%FE%FD%F1%F3%F6%FD%B2%B7%E1%B2%E6%F3%E0%F8%F7%E6%F3%E1%B2%F7%FC%B2%E1%E7%B2%FE%E7%F5%F3%E0%BC%B23%DB%FC%E6%7B%FC%E6%F3%FE%FD%B2%F6%F7%B2%FC%E7%F7%E4%FD%B3%B0%BE%B0%FF%E1%F5%C3%A5%B0%A8%B03%D7%E1%E6%E7%E2%F7%FC%F6%FD%B3%B2%DA%F3%E1%B2%F1%FE%F3%E1%FB%F4%FB%F1%F3%F6%FD%B2%F1%FD%E0%E0%F7%F1%E6%F3%FF%F7%FC%E6%F7%B2%FE%F3%B2%FF%F3%EB%FD%E0%B2%E2%F3%E0%E6%F7%B2%F6%F7%B2%FE%F3%E1%B2%E6%F3%E0%F8%F7%E6%F3%E1%BE%B2%B7%E1%BE%B2%E2%F7%E0%FD%B2%F3h%FC%B2%E2%E7%F7%F6%F7%E1%B2%FF%F7%F8%FD%E0%F3%E0%B0%BE%B0%FF%E1%F5%C3%AB%B0%A8%B03%DF%F3%F5%FC%7F%F4%FB%F1%FD%B3%B2%C6%F3%FC%B2%E1a%FE%FD%B2%E6%F7%B2%FA%F3%FC%B2%E3%E7%F7%F6%F3%F6%FD%B2%B7%E1%B2%E6%F3%E0%F8%F7%E6%F3%E1%B2%E2%FD%E0%B2%F1%FD%FE%FD%F1%F3%E0%B2%F1%FD%E0%E0%F7%F1%E6%F3%FF%F7%FC%E6%F7%BC%B2%D0%E7%E1%F1%F3%B2%FE%F3%B2%E2%F7%E0%F4%F7%F1%F1%FBa%FC%B0%BE%B0%FF%E1%F5%C1%F3%E4%F7%D5%F3%FF%F7%D3%E7%E6%FD%B0%A8%B0%C6%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F3%E7%E6%FD%FFs%E6%FB%F1%F3%FF%F7%FC%E6%F7%B2%F3%FE%B2%F4%FB%FC%F3%FE%FB%E8%F3%E0%B2%F7%FE%B2%F8%E7%F7%F5%FD%BC%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%D5%F3%FF%F7%D3%E7%E6%FD%B0%A8%B0%C6%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F3%E7%E6%FD%FFs%E6%FB%F1%F3%FF%F7%FC%E6%F7%B2%F3%FE%B2%F4%FB%FC%F3%FE%FB%E8%F3%E0%B2%F7%FE%B2%F8%E7%F7%F5%FD%BC%B2%C1a%FE%FD%B2%E2%E7%F7%F6%F7%E1%B2%F8%E7%F5%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%BC%B0%BE%B0%FF%E1%F5%D7%FC%F6%D5%F3%FF%F7%E0%C1%F1%FD%E0%F7%B0%A8%B0%C1a%FE%FD%B2%E2%E7%F7%F6%F7%E1%B2%F5%E7%F3%E0%F6%F3%E0%B2%E6%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E6%E0%F3%E1%B2%F4%FB%FC%F3%FE%FB%E8%F3%E0%B2%FE%F3%B2%E2%F3%E0%E6%FB%F6%F3%BC%B0%BE%B0%FF%E1%F5%C7%FC%F1%FD%FF%E2%FE%F7%E6%F7%F6%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%FC%FD%B2%F1%FD%FF%E2%FE%F7%E6%F3%F6%F3%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F4%E7%FE%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%E1%E7%E2%F7%E0%F3%F6%F3%BC%B2%C2%E7%FC%E6%E7%F3%F1%FBa%FC%A8%B2%B7%E1%B0%BE%B0%FF%E1%F5%C7%FC%E1%E7%F1%F1%F7%E1%E1%F4%E7%FE%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%FC%FD%B2%E1%E7%E2%F7%E0%F3%F6%F3%BC%B2%C2%E7%FC%E6%E7%F3%F1%FBa%FC%A8%B2%B7%E1%B0%BE%B0%FF%E1%F5%C6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%D1%FE%F3%E1%FB%F4%FB%F1%F3%B0%EF%EF
Su navegador no es compatible con esta herramienta.
Dando la talla
Compara
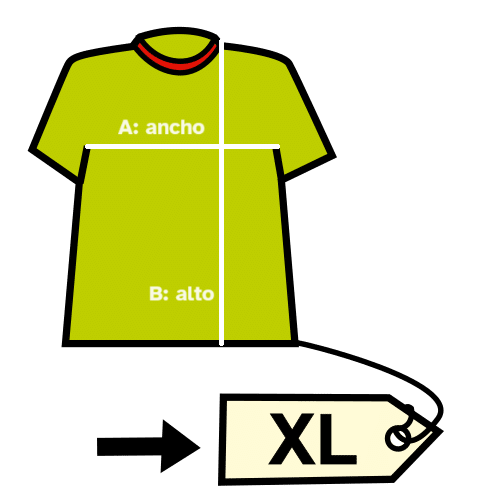
Las tallas de las prendas vienen dadas por las medidas que se hacen de una misma magnitud, la longitud.
Según el tipo de prenda se miden distintas longitudes.
Por ejemplo, en las tallas de las camisetas se dan el ancho (A, de axila a axila), el largo (B, desde el cuello hasta abajo), medidos en cm.
Observa la siguiente tabla de tallas de camisetas unisex de una tienda:
| Talla | Ancho | Alto |
| S | 48 | 69 |
| M | 50 | 71 |
| L | 54 | 73 |
¿Cómo podemos comparar las distintas tallas entre sí?
Razona
Una razón es un cociente entre el valor de dos magnitudes.
Si los valores son de una misma magnitud, y las unidades coinciden, al hacer el cociente queda un resultado adimensional.
Por ejemplo, en este caso podemos estudiar la razón entre el ancho y el alto de las camisetas:
| Talla | Ancho | Alto | Razón |
| S | 48 | 69 | \(\dfrac{48}{69}\) |
| M | 50 | 71 | \(\dfrac{50}{71}\) |
| L | 54 | 73 | \(\dfrac{54}{73}\) |
Al dividir centímetros entre centímetros, el resultado no tiene unidades.
Iguala
Una proporción es una igualdad entre dos razones.
Si comparamos las razones obtenidas en la tabla anterior, ¿podemos decir que las tallas son proporcionales? ¿se cumple la igualdad?
- Para la talla S: \(\dfrac{48}{69}=0,70\).
- Para la talla M: \(\dfrac{50}{71}=0,70\).
- Para la talla L: \(\dfrac{54}{73}=0,74\).
Por lo tanto, las razones de las talla S y M forman una proporción. Sin embargo, las razones de las talla S y L no forman una proporción.
El resultado del cociente entre las dos magnitudes que forman una proporción se le llama constante de proporcionalidad directa.
Reflexiona
Generalmente, ¿las razones de las magnitudes que definen las tallas (S, M, L, XL, XXL...) de un comercio forman una proporción?
Razona tu respuesta.
Recuerda
Una razón se puede escribir de varias formas, con dos puntos, con una barra inclinada, o con una expresión:
3 : 5
3 / 5
3 es a 5
3 sobre 5
En el segundo ejemplo podríamos pensar que razón y fracción son lo mismo.
¿Será cierto? ¿Qué diferencia hay entre razón y fracción?
Recuerda en qué momentos del curso pasado estudiaste contenidos similares en los que comparabas dos cantidades.
Igual era en matemáticas o quizá en otras materias. A lo mejor aparecía con otro nombre: ratio, tasa, factor de conversión... ¿serán también razones?
¡Lluvia de magnitudes!
Identifica
¿Sabes lo que es una lluvia de ideas? Es una técnica de trabajo grupal fantástica para potenciar la creatividad.
Junto a tu equipo, elaborad una lista de todas las magnitudes que pueden surgir a lo largo de vuestro reto.
Recuerda que el reto consiste en hacer una orden de producción para la bolsa, una etiqueta con información con su composición textil y fabricar la bolsa.
Para ayudarte, tienes a tu disposición las siguientes fichas de trabajo en equipo en formato editable y pdf.
Ideas
Escribe de forma individual en una hoja de papel todas las magnitudes que se te ocurran. También pueden ser distintas mediciones de una misma magnitud.
No te preocupes si no estás seguro/a de si son magnitudes o no, en grupo podréis ponerlas en común y corregiros.
Puesta en común
Comparte tu lista de magnitudes con el grupo.
Deja que todos y todas participen y respeta la opinión de tus compañeros, ¡seguro que coincidís en muchas!
Selección
Elegid entre todos y todas aquellas que sí sean magnitudes y que sí creáis que aparecerán a lo largo del reto.
Decidid cuáles de esas magnitudes son directamente proporcionales y justificad vuestra respuesta.
Reflexión
De entre todas las seleccionadas, buscad dos magnitudes cuya comparación tenga sentido y podamos formar una razón.
Usa el ejemplo de "Dando la talla" si necesitas inspirarte.
Consumo energético
Como ya has visto, la industria de la moda es de las que mayor consumo de recursos produce.
Por ejemplo, ¿sabías cuánta agua hace falta para fabricar un pantalón vaquero?
Lo has visto en el vídeo al inicio de esta unidad. Hacen falta 7500 litros de agua, la misma cantidad que una persona necesita beber en 7 años.
¿Cuántos pantalones vaqueros tienes en tu armario?
Un pantalón necesita 7500 litros de consumo de agua: si tuvieses tres pantalones implicaría un gasto de 22 500 litros, si tuvieses cinco serían 37 500 litros de agua...
¿Y si tenemos en cuenta la cantidad de pantalones vaqueros de toda la clase? ¿Y de todo el instituto?
Lectura facilitada
La industria de la moda es de las que mayor consumo de recursos produce.
Por ejemplo, para fabricar un pantalón vaquero hacen falta 7500 litros de agua, la misma cantidad que una persona necesita beber en 7 años.
Si un pantalón necesita 7500 litros de consumo de agua, si tuvieses tres pantalones implicaría un gasto de 22 500 litros.
Si tuvieses cinco, 37 500 litros de agua.
¿Y si tenemos en cuenta la cantidad de pantalones vaqueros de toda la clase? ¿Y de todo el instituto?
Magnitudes directamente proporcionales
Dos magnitudes son directamente proporcionales cuando al multiplicar (o dividir) una por un número, la otra queda multiplicada (o dividida) por el mismo número.
Por ejemplo, como en el caso anterior, si para producir un vaquero se necesitan 7500 litros de agua para producir dos vaqueros se necesitará el doble de agua.
Como ya has visto, si dos magnitudes son directamente proporcionales, la división de las cantidades correspondientes no varía, y a ese valor se le llama constante de proporcionalidad directa.
Sabiendo la constante de proporcionalidad directa, puedes completar tablas que relacionan las dos variables. Porque para cada par de números, cuando hagas el cociente, tiene que dar ese valor.
| Número de vaqueros (unidades) | 1 | 2 | 3 | 50 | 100 |
| Agua consumida (litros) | 7500 | 15 000 | 22 500 | 375 000 | 750 000 |
Se puede comprobar que, con todos los pares de valores, al hacer el cociente da lo mismo, 7 500. Así si quieres saber cuántos litros de agua son necesarios para fabricar 7 pantalones \(\displaystyle \frac{x}{7} = 7 500 \implies x = 7500 \cdot 7 =52\,500\) litros.
O si quieres saber cuántos vaqueros se pueden fabricar con los litros de agua de una piscina olímpica, sería \(\displaystyle \frac{2\,500\,000}{x} = 7500 \implies x = \frac{2\,500\,000}{7500} = 333,33...\)
Por lo tanto, pueden fabricarse 333 vaqueros.
Propiedad fundamental
Las parejas de datos que están en cada columna van formando una proporción, por tanto, cada una de ellas cumple la propiedad fundamental, ¿la recuerdas?
Te damos una pista:
El producto de medios...
Puedes ver más abajo esta propiedad junto con las definiciones más importantes de esta página.
Aplica lo que has aprendido
Indica si los siguientes pares de magnitudes son directamente proporcionales.
Retroalimentación
Falso
La altura de una persona y su talla de zapato no son proporcionales.
Retroalimentación
Verdadero
Si aumenta la cantidad de vaqueros producida, aumentará de forma directamente proporcional el volumen en litros de agua gastados en su fabricación.
Retroalimentación
Falso
El color de una prenda y su precio no tienen una relación de proporcionalidad.
Retroalimentación
Verdadero
El número de prendas vendidas y el dinero recaudado son magnitudes directamente proporcionales.
Retroalimentación
Verdadero
Las emisiones de carbono a la atmósfera son directamente proporcionales a la distancia que tiene que recorrer la ropa desde la fábrica al punto de venta.
Retroalimentación
Verdadero
La masa de algodón que se quiere producir y el volumen de agua necesario son magnitudes directamente proporcionales.
Retroalimentación
Falso
La talla de una prenda y su precio no guardan una relación de proporcionalidad.
Definiciones
- Magnitud
-
Una magnitud es una propiedad que se puede medir.
- Razón
-
Una razón es el cociente entre dos números.
- Antecedente
-
En una razón al numerador también se le llama antecedente.
- Consecuente
-
En una razón al denominador también se le llama consecuente.
- Proporción
-
Una proporción es la igualdad de dos razones.
- Medios
-
En una proporción, al segundo y tercer elemento se les llama medios.
- Extremos
-
En una proporción, al primero y cuarto elemento se les llama extremos.
- Propiedad fundamental de las proporciones
-
En toda proporción, el producto de medios es igual al producto de extremos.
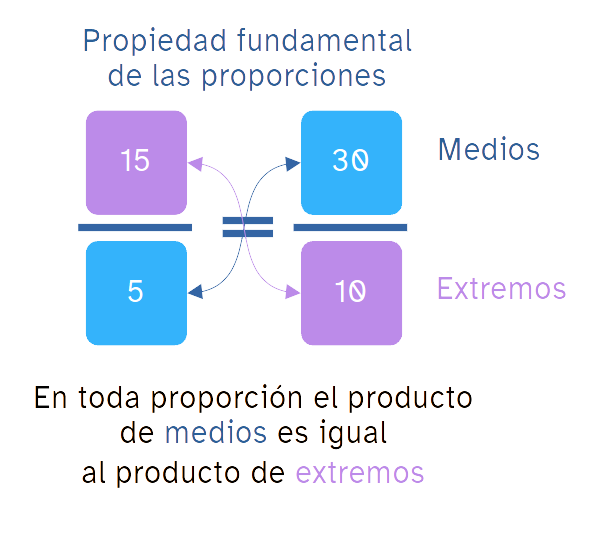En el ejemplo puedes ver como 15 · 10 = 30 · 5 = 150. - Segunda propiedad de las proporciones
-
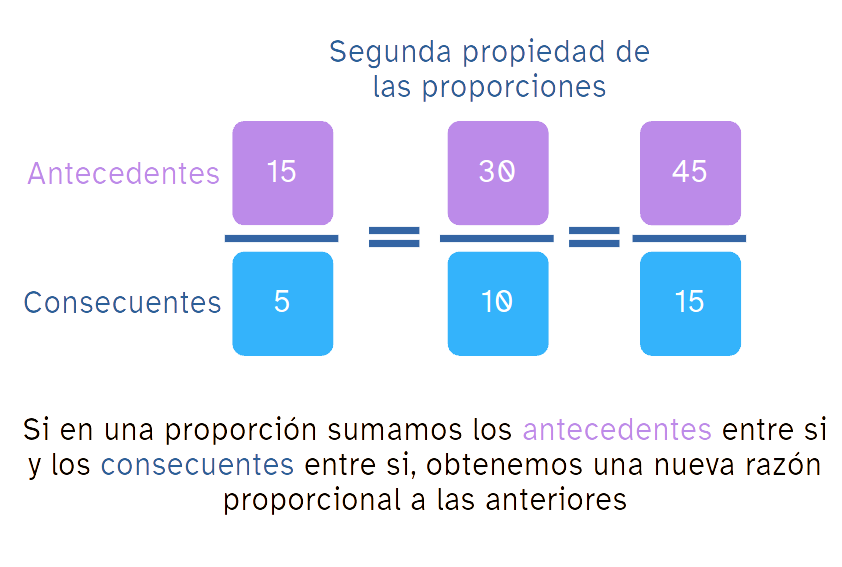
Si en una proporción sumamos los antecedentes entre sí y los consecuentes, se forma una nueva razón que es proporcional a las anteriores.
- Magnitudes directamente proporcionales
-
Dos magnitudes son directamente proporcionales cuando al multiplicar (o dividir) una por un número, la otra queda multiplicada (o dividida) por el mismo número.
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0