Partida de dardos

Después de un par de horas hablando de matemáticas, Xurxo e Iria necesitan un descanso.
Al fondo de la cafetería pueden ver una diana para jugar a dardos. Mientras esperan a que les sirvan la comida deciden jugar una partida.
-Estoy segura de que te gano, Xurxo, practiqué mucho con mi abuelo cuando era pequeña -dijo Iria. -Eso habrá que verlo -respondió Xurxo. Soy un experto en el lanzamiento de dardos.
Acertando en la diana
Observa en la siguiente imagen las puntuaciones de la partida. La zona roja vale 5 puntos, la naranja 10 y la azul 20.
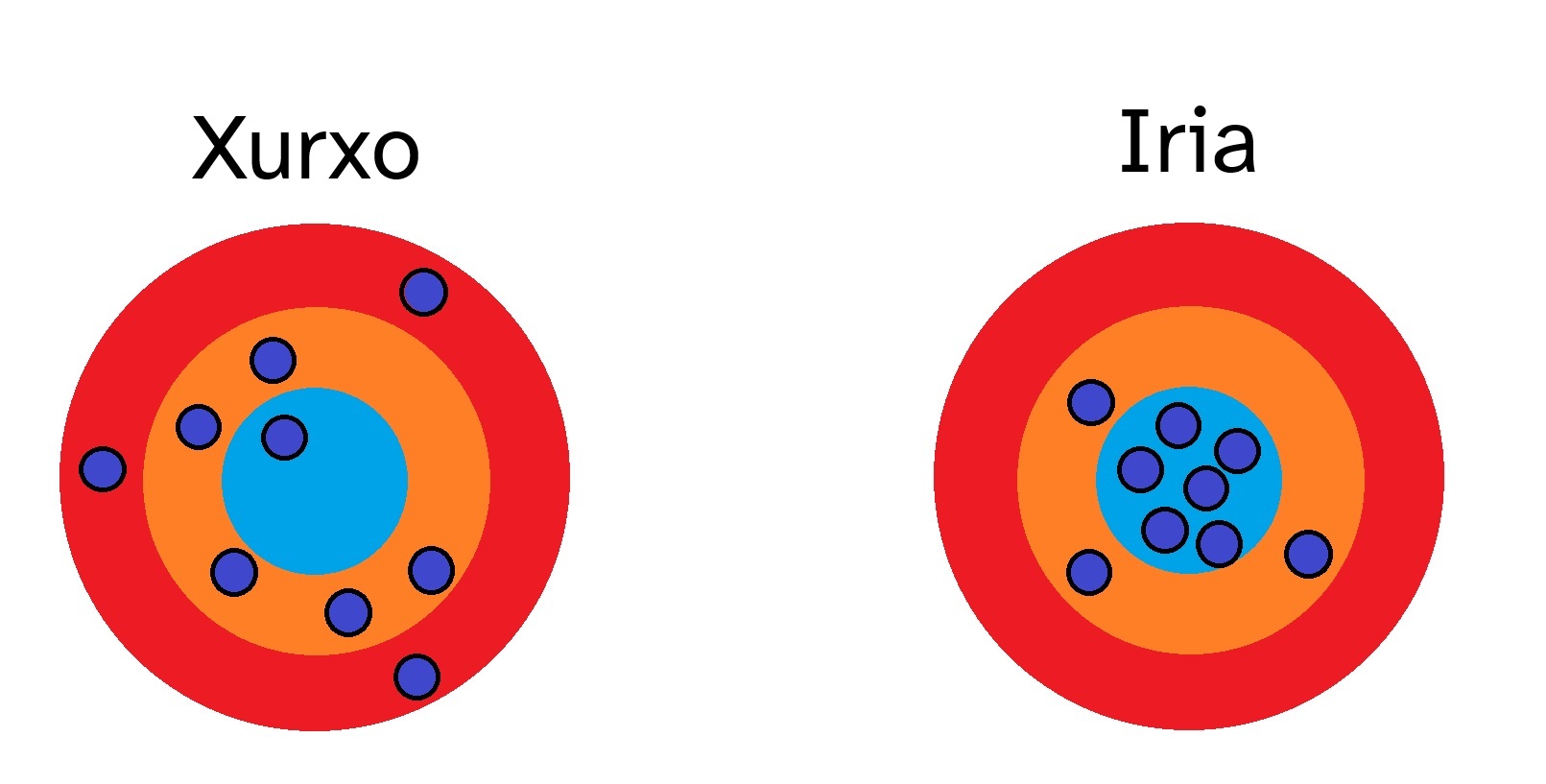
¿Cuál de ellos ha sido el mejor? ¿En qué te basas para dar esa respuesta?
Comparando resultados
Está claro que Iria ha ganado la partida porque la puntuación ha sido mayor.
En la precisión tampoco hay duda. Mirando las gráficas parece que Iria ha sido más precisa que Xurxo porque sus puntos están más aglutinados alrededor del centro de la diana.
Visualmente parece que la dispersión de Iria fue menor.
¿Es cierto esto? ¿Podemos verificarlo matemáticamente?
Diana 1 (Xurxo)
Las puntuaciones obtenidas por Xurxo fueron: 5, 5, 5, 10, 10, 10, 10, 10 y 20
La media es \(\bar{x}= \frac{\sum_{}^{}x_{i}\cdot f_{i}}{N}=\frac{5\cdot 3 +10\cdot 5 +20 }{9}=9,44\,puntos\)
La varianza es \(Var=\frac{\sum (x_{i}-\bar{x})^2\cdot f_{i}}{N}=\frac{(5-9,44)^2\cdot3+(10-9,44)^2\cdot5+(20-9,44)^2}{9}=\frac{177,22}{9}=19,13\, puntos^2\)
La desviación típica es \(\sigma =\sqrt{Var}=4,37 \,puntos\)
Diana 2 (Iria)
Las puntuaciones obtenidas por Iria fueron: 10, 10, 10, 20, 20, 20, 20, 20 y 20
La media es \(\bar{x}= \frac{\sum_{}^{}x_{i}\cdot f_{i}}{N}=\frac{10\cdot 3 +20\cdot 6 }{9}=16,67 \,puntos\)
La varianza es \(Var=\frac{\sum (x_{i}-\bar{x})^2\cdot f_{i}}{N}=\frac{(10-16,67)^2\cdot3+(20-16,67)^2\cdot6}{9}=\frac{200}{9}=22,22 \,puntos^2\)
La desviación típica es \(\sigma =\sqrt{Var}=4,71\, puntos\)
Comparando partidas
Los resultados parecen contradecir lo que vemos en las dianas.
Ambos han obtenido desviaciones típicas parecidas: 4,37 para Xurxo y 4,71 en para Iria, y numéricamente la de Iria es mayor que la de Xurxo.
¿Qué está pasando? ¿nos engaña la vista?
La razón es la solución
La respuesta es que no, la vista no nos engaña, pero antes de comparar dos conjuntos de datos hay que saber cómo hacerlo.
- Los resultados de la partida de Xurxo tienen una desviación de 4,37 que, comparada con su media 9,44 es grande, eso significa que hay una dispersión significativa respecto de la media.
- En la partida de Iria, la desviación es de 4,71 pero su media es 16,67, lo que significa que sus resultados están más cerca de la media; hay una menor variabilidad relativa respecto a su media.
Recuerda que la desviación típica mide la separación de los datos respecto su media, por tanto no tiene sentido comparar datos con medias tan diferentes.
La solución está en buscar un cálculo que elimine estas dificultades.
Para eso recurrimos a una razón, dividimos la desviación típica de los resultados de cada partida entre su media, obteniendo un valor sin unidades que sí podemos comparar entre partidas diferentes.
El resultado de esta división se llama coeficiente de variación.


