Números hasta en los hela2

Es hora de comenzar a planificar tu proyecto...
- ¿Cuánto dinero vas a destinar a comprar distintos tipos de leche?
- ¿Qué parte a comprar fruta?
- ¿Qué fracción de cada ingrediente llevarán tus recetas?
- ¿Cómo distribuirás el espacio de la estantería?
Empieza refrescando conceptos básicos que ya trabajaste en cursos anteriores.
Lectura facilitada
Es hora de comenzar a planificar tu proyecto...
- ¿Cuánto dinero será para leche?
- ¿Qué parte para fruta?
- ¿Qué fracción de cada ingrediente llevarán tus recetas?
- ¿Cómo distribuirás el espacio de la estantería?
Decimales
Un número decimal es un número que está compuesto por dos partes separadas por una coma:
- Parte entera: las cifras situadas a la izquierda de la coma.
- Parte decimal: las cifras situadas a la derecha de la coma.
Por ejemplo, los siguientes números son números decimales:
2,34 43,5 8,1234
Fracciones
Una fracción es una expresión de la forma \(\dfrac{a}{b}\), donde \(a\) y \(b\) son números enteros siendo \(b \neq 0\).
Las fracciones tienen distintas interpretaciones según el contexto en el que las uses:
Parte de la unidad
Una fracción puede ser una o varias de las partes enteras en las que se divide una unidad. Está formada por:
- El denominador indica las partes iguales en las que se divide la unidad.
- El numerador indica cuántas de esas partes estamos considerando.
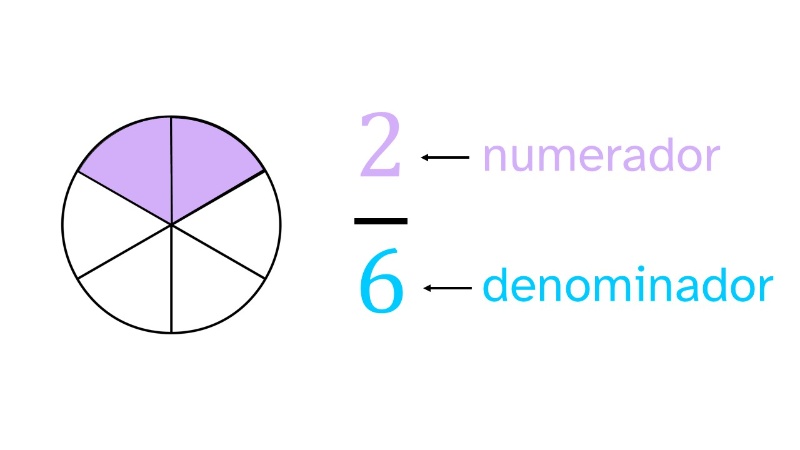
Por ejemplo, si los ingredientes de un batido se dividen en seis partes iguales y dos son de fresa, la fracción anterior, \(\dfrac{2}{6}\), representa la cantidad de dicha fruta en el batido.
Un cociente
Una fracción puede interpretarse como el cociente entre dos números, el numerador entre el denominador.
Por ejemplo, si repartimos 3 litros de batido entre 4 vasos, la fracción que corresponde a cada vaso es tres cuartos de litro o 75 centilitros:
\(\dfrac{3}{4} = 0,75\text{ l }= 75\text{ cl}\)
¡OJO! El denominador de una fracción siempre es un número distinto de cero.
Un operador
Una fracción se puede interpretar como un operador que actúa sobre una cantidad: multiplica por el numerador y divide entre el denominador.
Por ejemplo, para calcular las dos quintas partes de 50 cl de batido haríamos lo siguiente:
\(\dfrac{2}{5}\text{ de }50 = \dfrac{2}{5}\cdot 50 = \dfrac{2\cdot 50} {5}= \dfrac{100}{5}=20\text{ cl}\)





