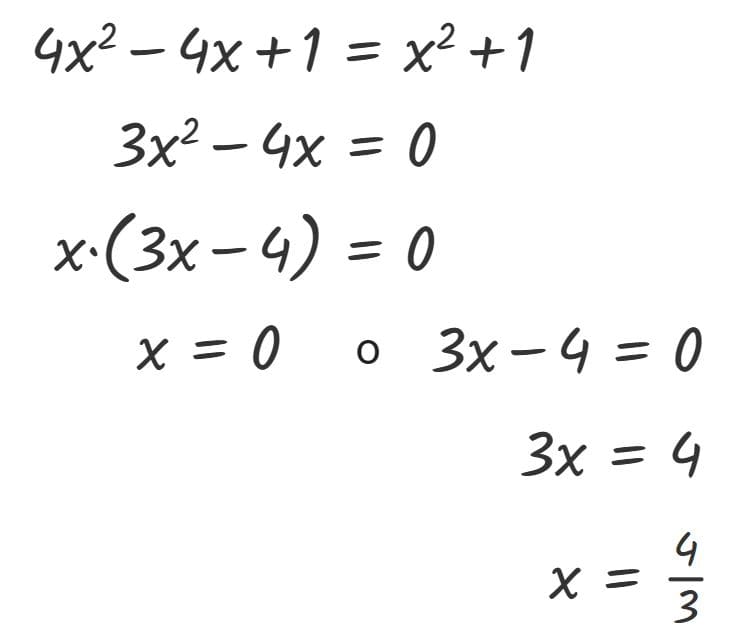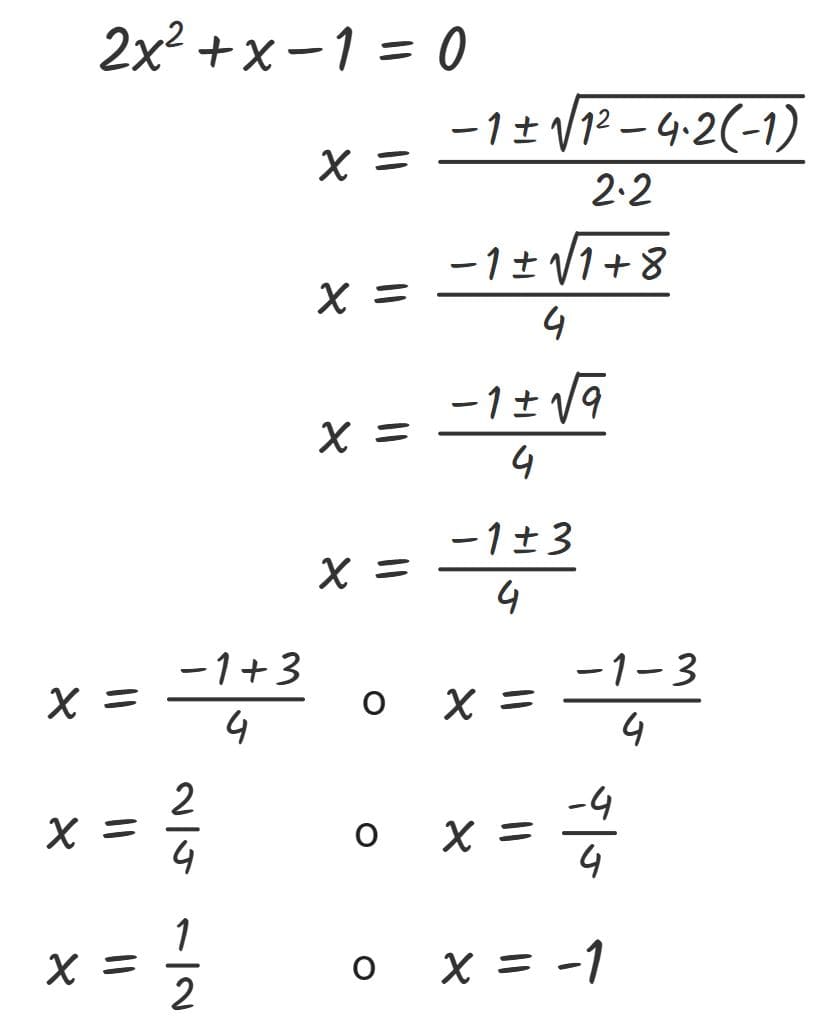Manual del detective: capítulo 3

Capítulo 3

Habiendo superado el ecuador de tu formación te habrás dado cuenta ya de la importancia del álgebra en este "mundillo".

En este capítulo profundizaremos en las ecuaciones de 2º grado, aquellas en las que la incógnita aparece elevada al cuadrado.

Esto será una herramienta más en tu arsenal de detective. Te permitirá abrir nuevas vías en tus investigaciones y comprender que puede existir más de una solución para el mismo problema en función del contexto.

¿Serás capaz de encontrar todas las soluciones?

Lectura facilitada

En este capítulo profundizaremos en las ecuaciones de 2º grado.

Esto será una herramienta más en tu arsenal de detective.

¿Serás capaz de encontrar todas las soluciones?

Ecuaciones de segundo grado

Una ecuación de segundo grado o ecuación cuadrática es una ecuación polinómica en la que el mayor exponente de la variable es dos. Se puede expresar de forma general como

\[ax^2+bx+c=0\]

donde \(a\), \(b\) y \(c\) son números cualesquiera, siendo \(a\neq 0\).

Resolviendo ecuaciones incompletas

Se llama ecuación de segundo grado incompleta a aquella en la que o \(b=0\) o \(c=0\).

Si b=0

Si b=0 la ecuación de segundo grado es de la forma \(ax^2+c=0\)

1) Despejas el término \(x^2\)

\[ax^2+c=0\Rightarrow ax^2=-c\Rightarrow x^2=\dfrac{-c}{a}\]

2) Aplicas la raíz cuadrada a ambos lados, teniendo en cuenta los dos posibles valores de esta (positivo y negativo)

\[x=\pm\sqrt{\dfrac{-c}{a}}\]

Por ejemplo,

\[x^2-13=-4\Rightarrow x^2-13+4=0\]

\[x^2-9=0\]

Es una ecuación incompleta de este tipo porque no tiene término de grado 1.

Se resolvería despejando \(x^2\) y aplicando raíces cuadradas, como se muestra en la imagen.

Si en alguna ecuación obtienes un número negativo dentro de la raíz cuadrada, entonces sabrás que esa ecuación no tiene solución real, ya que no es posible calcular raíces cuadradas de números negativos.

Si c=0

Si c=0 la ecuación de segundo grado es de la forma \(ax^2+bx=0\)

1) Extraes factor común

\[ax^2+bx=0\Rightarrow x\cdot (ax+b)=0\]

2) Por tratarse de una multiplicación que da como resultado 0, alguno de los dos factores debe ser 0. Debes igualar a 0 ambos factores.

\[x=0\]

\[ax+b=0\Rightarrow ax=-b \Rightarrow x=\dfrac{-b}{a}\]

Por ejemplo,

\[4x^2-4x+1=x^2+1 \Rightarrow 4x^2-4x+1-x^2-1=0\]

\[3x^2-4x=0\]

Es una ecuación incompleta de este tipo porque no tiene término independiente.

Se resolvería sacando factor común e igualando cada término a 0.

Así obtienes siempre una solución \(x=0\) y una ecuación de primer grado que ya sabes resolver. Mira la solución paso a paso en la imagen.

Ecuaciones incompletas

Resuelve las siguientes ecuaciones incompletas. Introduce las soluciones de menor a mayor.

%E9%B0%E6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%D1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FB%FC%E1%E6%E0%E7%F1%E6%FB%FD%FC%E1%B0%A8%B0%AE%E2%AC%C0%F7%E1%E7%F7%FE%E4%F7%B2%FE%F3%E1%B2%E1%FB%F5%E7%FB%F7%FC%E6%F7%E1%B2%F7%F1%E7%F3%F1%FB%FD%FC%F7%E1%B2%FB%FC%F1%FD%FF%E2%FE%F7%E6%F3%E1%BC%B2%DB%FC%E6%E0%FD%F6%E7%F1%F7%B2%FE%F3%E1%B2%E1%FD%FE%E7%F1%FB%FD%FC%F7%E1%B2%F6%F7%B2%FF%F7%FC%FD%E0%B2%F3%B2%FF%F3%EB%FD%E0%BC%AE%BD%E2%AC%B0%BE%B0%E6%F7%EA%E6%C6%F7%EA%E6%B0%A8%B0%B7%A1%D1%E2%B7%A1%D7%F3%B7%A0%AB%B7%A0%A2%B7%A7%D1%B7%A0%AA%EA%B7%A7%D7%A0%BF%A3%B7%A1%D6%A2%B7%A7%D1%C0%FB%F5%FA%E6%F3%E0%E0%FD%E5%B7%A7%D1%B7%A0%AB%B7%A0%A2%B7%A7%D1%B7%A0%AA%EA%B7%A1%D6%B7%A7%D1%B7%A0%AB%B7%A0%A2%D2%D2%BF%A3%D2%D2%B7%A0%D1%B7%A0%A2%B7%A7%D1%B7%A0%AA%EA%B7%A1%D6%B7%A7%D1%B7%A0%AB%B7%A0%A2%D2%D2%A3%D2%D2%B7%A1%D1%BD%E2%B7%A1%D7%B7%A2%D3%B7%A1%D1%E2%B7%A1%D7%F0%B7%A0%AB%B7%A0%A2%B7%A7%D1%B7%A0%AA%A0%EA%B7%A7%D7%A0%B9%A6%EA%B7%A1%D6%A2%B7%A7%D1%C0%FB%F5%FA%E6%F3%E0%E0%FD%E5%B7%A7%D1%B7%A0%AB%B7%D3%A2%B7%A7%D1%B7%A0%AA%EA%B7%A1%D6%B7%A7%D1%B7%A0%AB%B7%A0%A2%D2%D2%BF%A0%D2%D2%B7%A0%D1%B7%A0%A2%B7%A7%D1%B7%A0%AA%EA%B7%A1%D6%B7%A7%D1%B7%A0%AB%B7%A0%A2%D2%D2%A2%D2%D2%B7%A1%D1%BD%E2%B7%A1%D7%B7%A2%D3%B7%A1%D1%E2%B7%A1%D7%F1%B7%A0%AB%B7%A0%A2%B7%A7%D1%B7%A0%AA%EA%B7%A7%D7%A0%BF%A1%EA%B7%A1%D6%A2%B7%A7%D1%C0%FB%F5%FA%E6%F3%E0%E0%FD%E5%B7%A7%D1%B7%A0%AB%B7%D3%A2%B7%A7%D1%B7%A0%AA%EA%B7%A1%D6%B7%A7%D1%B7%A0%AB%B7%A0%A2%D2%D2%A2%D2%D2%B7%A0%D1%B7%A0%A2%B7%A7%D1%B7%A0%AA%EA%B7%A1%D6%B7%A7%D1%B7%A0%AB%B7%A0%A2%D2%D2%A1%D2%D2%B7%A1%D1%BD%E2%B7%A1%D7%B7%A2%D3%B7%A1%D1%E2%B7%A1%D7%F6%B7%A0%AB%B7%D3%A2%B7%A0%A2%B7%A7%D1%B7%A0%AA%EA%B7%A7%D7%A0%BF%A3%A4%B7%A1%D6%A2%B7%A7%D1%C0%FB%F5%FA%E6%F3%E0%E0%FD%E5%B7%A7%D1%B7%A0%AB%B7%A0%A2%B7%A7%D1%B7%A0%AA%EA%B7%A1%D6%B7%A7%D1%B7%A0%AB%B7%A0%A2%D2%D2%BF%A6%D2%D2%B7%A0%D1%B7%A0%A2%B7%A7%D1%B7%A0%AA%EA%B7%A1%D6%B7%A7%D1%B7%A0%AB%B7%A0%A2%D2%D2%A6%D2%D2%B7%A1%D1%BD%E2%B7%A1%D7%B0%BE%B0%E1%FA%FD%E5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%FB%E6%FB%FC%F7%E0%F3%E0%EB%B0%A8%E9%B0%E1%FA%FD%E5%D1%FE%E7%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FE%E7%F7%D5%F3%FF%F7%B0%A8%B0%C0%D3_%C8%B0%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F5%F7%D1%FE%E7%F7%B0%A8%A7%A2%BE%B0%E1%FA%FD%E5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%F4%F3%FE%E1%F7%BE%B0%F1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%BE%B0%FF%F7%E1%E1%F3%F5%F7%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%B0%EF%BE%B0%F1%F3%E1%F7%C1%F7%FC%E1%FB%E6%FB%E4%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%FB%E1%C1%F1%FD%E0%FF%B0%A8%A3%BE%B0%E6%F7%EA%E6%D0%E7%E6%E6%FD%FC%C1%F1%FD%E0%FF%B0%A8%B0%D5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%E0%F7%E2%F7%F3%E6%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%E6%E0%E7%F7%BE%B0%E6%F7%EA%E6%D4%F7%F7%F6%D0%F3%F1%F9%B0%A8%B0%B0%BE%B0%E6%F7%EA%E6%D3%F4%E6%F7%E0%B0%A8%B0%B0%BE%B0%F4%F7%F7%F6%D0%F3%F1%F9%B0%A8%F4%F3%FE%E1%F7%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F8%F7%D4%D0%B0%A8%A3%A2%A2%BE%B0%E4%F7%E0%E1%FB%FD%FC%B0%A8%A3%BE%B0%F7%E1%E6%E0%FB%F1%E6%D1%FA%F7%F1%F9%B0%A8%F4%F3%FE%E1%F7%BE%B0%E5%FD%E0%F6%E1%C1%FB%E8%F7%B0%A8%F4%F3%FE%E1%F7%BE%B0%E6%FB%FF%F7%B0%A8%A2%BE%B0%E6%EB%E2%F7%B0%A8%A2%BE%B0%E5%FD%E0%F6%E1%D7%E0%E0%FD%E0%E1%B0%A8%B0%B0%BE%B0%F3%E6%E6%F7%FF%E2%E1%DC%E7%FF%F0%F7%E0%B0%A8%A7%BE%B0%E2%F7%E0%F1%F7%FC%E6%F3%F8%F7%D7%E0%E0%FD%E0%B0%A8%A0%A2%BE%B0%E1%FA%FD%E5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%E6%E0%E7%F7%BE%B0%E5%FD%E0%F6%E1%DE%FB%FF%FB%E6%B0%A8%F4%F3%FE%E1%F7%BE%B0%F7%E4%F3%FE%E7%F3%E6%FB%FD%FC%B0%A8%F4%F3%FE%E1%F7%BE%B0%F7%E4%F3%FE%E7%F3%E6%FB%FD%FC%DB%D6%B0%A8%B0%B0%BE%B0%FB%F6%B0%A8%B0%A0%A2%A0%A7%A3%A3%A0%A0%A2%A6%AB%A6%A3%BF%A4%A2%B0%BE%B0%FF%E1%F5%E1%B0%A8%E9%B0%FF%E1%F5%DA%F3%E2%E2%F7%FC%B0%A8%B0%C2%F3%E1%F3%E0%B0%BE%B0%FF%E1%F5%C0%F7%E2%FE%EB%B0%A8%B0%C0%F7%E1%E2%FD%FC%F6%F7%E0%B0%BE%B0%FF%E1%F5%C1%E7%F0%FF%FB%E6%B0%A8%B0%D7%FC%E4%FB%F3%E0%B0%BE%B0%FF%E1%F5%D7%FC%E6%F7%E0%D1%FD%F6%F7%B0%A8%B0%DB%FC%E6%E0%FD%F6%E7%E8%F1%F3%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%D1%FD%F6%F7%B0%A8%B0%D7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B2%FC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B0%BE%B0%FF%E1%F5%D5%F3%FF%F7%DD%E4%F7%E0%B0%A8%B03%D4%FB%FC%B2%F6%F7%B2%FE%F3%B2%E2%F3%E0%E6%FB%F6%F3%B3%B0%BE%B0%FF%E1%F5%DB%FC%F6%FB%F1%F3%E6%F7%C5%FD%E0%F6%B0%A8%B0%C2%E0%FD%E2%FD%E0%F1%FB%FD%FC%F7%B2%E7%FC%F3%B2%E2%F3%FE%F3%F0%E0%F3%B2%FD%B2%F7%EA%E2%E0%F7%E1%FBa%FC%B0%BE%B0%FF%E1%F5%D1%FE%E7%F7%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B2%DE%F3%B2%E2%FB%E1%E6%F3%B2%F7%E1%A8%B0%BE%B0%FF%E1%F5%CB%FD%E7%DA%F3%E1%B0%A8%B0%C6%FB%F7%FC%F7%B2%B7%A3%B2%F3%F1%FB%F7%E0%E6%FD%E1%B2%EB%B2%B7%A0%B2%F4%F3%FE%FE%FD%E1%B0%BE%B0%FF%E1%F5%D1%FD%F6%F7%D3%F1%F1%F7%E1%E1%B0%A8%B0%D1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%D3%F5%F3%FB%FC%B0%A8%B0%C4%FD%FE%E4%F7%E0%B2%F3%B2%E2%E0%FD%F0%F3%E0%B0%BE%B0%FF%E1%F5%C0%F7%E3%E7%FB%E0%F7%F6%D3%F1%F1%F7%E1%E1%D9%F7%EB%B0%A8%B0%D7%E1%B2%FC%F7%F1%F7%E1%F3%E0%FB%FD%B2%F7%FE%B2%F1a%F6%FB%F5%FD%B2%F6%F7%B2%F3%F1%F1%F7%E1%FD%B0%BE%B0%FF%E1%F5%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%DE%FD%FD%F9%FB%FC%F5%B0%A8%B03%D5%F7%FC%FB%F3%FE%B3%B2%DE%F3%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%B2%E3%E7%F7%B2%F7%E1%E6%F3%F0%F3%B2%F0%E7%E1%F1%F3%FC%F6%FD%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%E6%F3%E0%E6%B0%A8%B0%C2%E7%FE%E1%F3%B2%F3%E3%E7%7F%B2%E2%F3%E0%F3%B2%F7%FF%E2%F7%E8%F3%E0%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%E1%B0%A8%B0%D7%E0%E0%FD%E0%F7%E1%B0%BE%B0%FF%E1%F5%D7%E0%E0%FD%E0%B0%A8%B0%D7%E0%E0%FD%E0%B0%BE%B0%FF%E1%F5%DF%FD%E4%F7%DD%FC%F7%B0%A8%B0%C2%F3%E1%F3%E0%B0%BE%B0%FF%E1%F5%DA%FB%E6%E1%B0%A8%B0%D3%F1%FB%F7%E0%E6%FD%E1%B0%BE%B0%FF%E1%F5%DA%FB%E6%B0%A8%B0%D3%F1%FB%F7%E0%E6%FD%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%DF%FB%FC%FB%FF%FB%E8%F7%B0%A8%B0%DF%FB%FC%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%DF%F3%EA%FB%FF%FB%E8%F7%B0%A8%B0%DF%F3%EA%FB%FF%FB%E8%F3%E0%B0%BE%B0%FF%E1%F5%C6%FB%FF%F7%B0%A8%B0%DE%7F%FF%FB%E6%F7%B2%F6%F7%B2%E6%FB%F7%FF%E2%FD%B2%BA%FF%FF%A8%E1%E1%BB%B0%BE%B0%FF%E1%F5%DE%FB%E4%F7%B0%A8%B0%C4%FB%F6%F3%B0%BE%B0%FF%E1%F5%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C2%F3%FC%E6%F3%FE%FE%F3%B2%D1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%D7%EA%FB%E6%D4%E7%FE%FE%C1%F1%E0%F7%F7%FC%B0%A8%B0%C1%F3%FE%FB%E0%B2%F6%F7%FE%B2%FF%FD%F6%FD%B2%E2%F3%FC%E6%F3%FE%FE%F3%B2%F1%FD%FF%E2%FE%F7%E6%F3%B0%BE%B0%FF%E1%F5%DC%E7%FF%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%B0%DCh%FF%F7%E0%FD%B2%F6%F7%B2%E2%E0%F7%F5%E7%FC%E6%F3%E1%B0%BE%B0%FF%E1%F5%DC%FD%DB%FF%F3%F5%F7%B0%A8%B0%C2%E0%F7%F5%E7%FC%E6%F3%B2%E1%FB%FC%B2%FB%FFs%F5%F7%FC%F7%E1%B0%BE%B0%FF%E1%F5%D1%FD%FD%FE%B0%A8%B03%D0%FB%F7%FC%B3%B0%BE%B0%FF%E1%F5%DE%FD%E1%F7%C6%B0%A8%B0%DA%F3%B2%E2%F7%E0%F6%FB%F6%FD%B2%A1%A1%A2%B2%E2%E7%FC%E6%FD%E1%B0%BE%B0%FF%E1%F5%DE%FD%E1%F7%DE%FB%E4%F7%B0%A8%B0%DA%F3%B2%E2%F7%E0%F6%FB%F6%FD%B2%E7%FC%F3%B2%E4%FB%F6%F3%B0%BE%B0%FF%E1%F5%DE%FD%E1%E6%DE%FB%E4%F7%E1%B0%A8%B03%DA%F3%B2%E2%F7%E0%F6%FB%F6%FD%B2%E6%FD%F6%F3%E1%B2%E1%E7%E1%B2%E4%FB%F6%F3%E1%B3%B0%BE%B0%FF%F5%E1%D3%FE%FE%C3%E7%F7%E1%E6%FB%FD%FC%E1%B0%A8%B03%D1%FD%FF%E2%FE%F7%E6%F3%F6%F3%E1%B2%FE%F3%E1%B2%E2%E0%F7%F5%E7%FC%E6%F3%E1%B3%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F7%E1%B0%A8%B03%D1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%D7%EA%F1%F7%FE%F7%FC%E6%F7%B3%B2%EE%B23%D5%F7%FC%FB%F3%FE%B3%B2%EE%B23%DF%E7%EB%B2%F0%FB%F7%FC%B3%B2%EE%B23%C2%F7%E0%F4%F7%F1%E6%FD%B3%B0%BE%B0%FF%E1%F5%D4%F3%FB%FE%E7%E0%F7%E1%B0%A8%B03%DC%FD%B2%F7%E0%F3%B2%F7%E1%FD%B3%B2%EE%B23%DB%FC%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DC%FD%B2%F7%E1%B2%F1%FD%E0%E0%F7%F1%E6%FD%B3%B2%EE%B23%DE%FD%B2%E1%F7%FC%E6%FB%FF%FD%E1%B3%B2%EE%B23%D7%E0%E0%FD%E0%B3%B0%BE%B0%FF%E1%F5%C6%E0%EB%D3%F5%F3%FB%FC%B0%A8%B0%DC%F7%F1%F7%E1%FB%E6%F3%B2%F3%FE%B2%FF%F7%FC%FD%E1%B2%E7%FC%B2%B7%E1%B7%B2%F6%F7%B2%E0%F7%E1%E2%E7%F7%E1%E6%F3%E1%B2%F1%FD%E0%E0%F7%F1%E6%F3%E1%B2%E2%F3%E0%F3%B2%F1%FD%FC%E1%F7%F5%E7%FB%E0%B2%FE%F3%B2%FB%FC%F4%FD%E0%FF%F3%F1%FBa%FC%BC%B2%C4%E7%F7%FE%E4%F3%B2%F3%B2%FB%FC%E6%F7%FC%E6%F3%E0%FE%FD%BC%B0%BE%B0%FF%E1%F5%C5%E0%FD%E6%F7%B0%A8%B0%D7%E1%F1%E0%FB%F0%F3%B2%FE%F3%B2%E2%F3%FE%F3%F0%E0%F3%B2%F1%FD%E0%E0%F7%F1%E6%F3%B2%EB%B2%E2%E7%FE%E1%F7%B2%F7%FC%B2%C0%F7%E1%E2%FD%FC%F6%F7%E0%BC%B2%C1%FB%B2%F6%E7%F6%F3%BE%B2%E2%E7%FE%E1%F7%B2%F7%FC%B2%C1%F7%F5%E7%FB%E0%BC%B0%BE%B0%FF%E1%F5%DC%FD%E6%DC%F7%E6%E5%FD%E0%F9%B0%A8%B0%D3%B2%F7%E1%E6%F7%B2%F8%E7%F7%F5%FD%B2%E1a%FE%FD%B2%E1%F7%B2%E2%E7%F7%F6%F7%B2%F8%E7%F5%F3%E0%B2%F1%FD%FC%B2%F1%FD%FC%F7%EA%FBa%FC%B2%F3%B2%FB%FC%E6%F7%E0%FC%F7%E6%BC%B0%BE%B0%FF%E1%F5%D7%FC%F6%D5%F3%FF%F7%C1%F1%FD%E0%F7%B0%A8%B0%D3%FC%E6%F7%E1%B2%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F1%FD%FF%FB%F7%FC%F1%F7%B2%FE%F3%B2%E2%F3%E0%E6%FB%F6%F3%BC%B0%BE%B0%FF%E1%F5%C1%F1%FD%E0%F7%C1%F1%FD%E0%FF%B0%A8%B0%DE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%FC%FD%B2%E1%F7%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%E2%FD%E0%E3%E7%F7%B2%F7%E1%E6%F3%B2%E2s%F5%FB%FC%F3%B2%FC%FD%B2%F4%FD%E0%FF%F3%B2%E2%F3%E0%E6%F7%B2%B2%F6%F7%B2%E7%FC%B2%E2%F3%E3%E7%F7%E6%F7%B2%C1%D1%DD%C0%DF%BC%B0%BE%B0%FF%E1%F5%C3%E7%F7%E1%E6%FB%FD%FC%B0%A8%B0%C2%E0%F7%F5%E7%FC%E6%F3%B0%BE%B0%FF%E1%F5%D3%FC%E1%E5%F7%E0%B0%A8%B0%C0%F7%E1%E2%FD%FC%F6%F7%E0%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%C1%F1%FD%E0%F7%B0%A8%B03%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E7%FC%F3%B2%E4%F7%E8%B3%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%B0%A8%B0%C1a%FE%FD%B2%E2%E7%F7%F6%F7%B2%F5%E7%F3%E0%F6%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%B0%BE%B0%FF%E1%F5%DB%FC%F4%FD%E0%FF%F3%E6%FB%FD%FC%B0%A8%B0%D1%FE%F3%E4%F7%B2%F6%F7%B2%F3%F1%E0%F7%F6%FB%E6%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%CB%FD%E7%C1%F1%FD%E0%F7%B0%A8%B0%C6%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B0%BE%B0%FF%E1%F5%D3%E7%E6%FA%FD%E0%B0%A8%B0%D3%E7%E6%FD%E0%7F%F3%B0%BE%B0%FF%E1%F5%DD%FC%FE%EB%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C6%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%BC%B2%C1a%FE%FD%B2%E2%E7%F7%F6%F7%E1%B2%F8%E7%F5%F3%E0%B2%E7%FC%F3%B2%E4%F7%E8%BC%B0%BE%B0%FF%E1%F5%C1%F3%E4%F7%D3%E7%E6%FD%B0%A8%B0%C6%E7%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E1%F7%B2%F5%E7%F3%E0%F6%F3%E0s%B2%F3%E7%E6%FD%FFs%E6%FB%F1%F3%FF%F7%FC%E6%F7%B2%F6%F7%E1%E2%E7%7B%E1%B2%F6%F7%B2%F1%F3%F6%F3%B2%E2%E0%F7%F5%E7%FC%E6%F3%BC%B0%BE%B0%FF%E1%F5%C1%F7%E4%F7%E0%F3%FE%C1%F1%FD%E0%F7%B0%A8%B0%C2%E7%F7%F6%F7%E1%B2%F5%E7%F3%E0%F6%F3%E0%B2%FE%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%E6%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%F1%FD%FF%FD%B2%E3%E7%FB%F7%E0%F3%B0%BE%B0%FF%E1%F5%CB%FD%E7%DE%F3%E1%E6%C1%F1%FD%E0%F7%B0%A8%B0%DE%F3%B2h%FE%E6%FB%FF%F3%B2%E2%E7%FC%E6%E7%F3%F1%FBa%FC%B2%F5%E7%F3%E0%F6%F3%F6%F3%B2%F7%E1%B0%BE%B0%FF%E1%F5%D3%F1%E6%FB%E6%EB%D1%FD%FF%E2%FE%EB%B0%A8%B0%CB%F3%B2%FA%F3%E1%B2%E0%F7%F3%FE%FB%E8%F3%F6%FD%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%BC%B0%BE%B0%FF%E1%F5%C2%FE%F3%EB%C1%F7%E4%F7%E0%F3%FE%C6%FB%FF%F7%E1%B0%A8%B0%C2%E7%F7%F6%F7%E1%B2%E0%F7%F3%FE%FB%E8%F3%E0%B2%F7%E1%E6%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%B2%F1%E7%F3%FC%E6%F3%E1%B2%E4%F7%F1%F7%E1%B2%E3%E7%FB%F7%E0%F3%E1%BC%B0%BE%B0%FF%E1%F5%D1%FE%FD%E1%F7%B0%A8%B0%D1%F7%E0%E0%F3%E0%B0%BE%B0%FF%E1%F5%DE%FD%F3%F6%FB%FC%F5%B0%A8%B0%D1%F3%E0%F5%F3%FC%F6%FD%BC%B2%D7%E1%E2%F7%E0%F7%BE%B2%E2%FD%E0%B2%F4%F3%E4%FD%E0%BC%BC%BC%B0%BE%B0%FF%E1%F5%C2%FD%FB%FC%E6%E1%B0%A8%B0%E2%E7%FC%E6%FD%E1%B0%BE%B0%FF%E1%F5%D3%E7%F6%FB%FD%B0%A8%B0%D3%E7%F6%FB%FD%B0%BE%B0%FF%E1%F5%C1%FD%FE%E7%E6%FB%FD%FC%B0%A8%B0%C1%FD%FE%E7%F1%FBa%FC%B0%BE%B0%FF%E1%F5%C6%E0%EB%B0%A8%B03%C2%E0%E7%F7%F0%F3%B2%FD%E6%E0%F3%B2%E4%F7%E8%B3%B0%BE%B0%FF%E1%F5%D1%FA%F7%F1%F9%B0%A8%B0%D1%FD%FF%E2%E0%FD%F0%F3%E0%B0%BE%B0%FF%E1%F5%D7%FC%F6%C1%F1%FD%E0%F7%B0%A8%B0%DA%F3%E1%B2%E6%F7%FC%FB%F6%FD%B2%B7%E1%B2%F3%F1%FB%F7%E0%E6%FD%E1%B2%EB%B2%B7%F6%B2%F7%E0%E0%FD%E0%F7%E1%BC%B0%BE%B0%FF%E1%F5%D7%FC%F6%C6%FB%FF%F7%B0%A8%B0%D7%FE%B2%E6%FB%F7%FF%E2%FD%B2%FA%F3%B2%F4%FB%FC%F3%FE%FB%E8%F3%F6%FD%BC%B0%BE%B0%FF%E1%F5%D5%F3%FF%F7%D7%FC%F6%B0%A8%B0%DA%F3%E1%B2%F1%FD%FF%E2%FE%F7%E6%F3%F6%FD%B2%FE%F3%B2%F3%F1%E6%FB%E4%FB%F6%F3%F6%B0%BE%B0%FF%E1%F5%C7%FC%F1%FD%FF%E2%FE%F7%E6%F7%F6%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%FC%FD%B2%F1%FD%FF%E2%FE%F7%E6%F3%F6%F3%B0%BE%B0%FF%E1%F5%C1%E7%F1%F1%F7%E1%E1%F4%E7%FE%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%E1%E7%E2%F7%E0%F3%F6%F3%BC%B2%C2%E7%FC%E6%E7%F3%F1%FBa%FC%A8%B2%B7%E1%B0%BE%B0%FF%E1%F5%C7%FC%E1%E7%F1%F1%F7%E1%E1%F4%E7%FE%D3%F1%E6%FB%E4%FB%E6%EB%B0%A8%B0%D3%F1%E6%FB%E4%FB%F6%F3%F6%B2%FC%FD%B2%E1%E7%E2%F7%E0%F3%F6%F3%BC%B2%C2%E7%FC%E6%E7%F3%F1%FBa%FC%A8%B2%B7%E1%B0%BE%B0%FF%E1%F5%C6%EB%E2%F7%D5%F3%FF%F7%B0%A8%B0%D1%FD%FF%E2%FE%F7%E6%F3%B0%EF%EF

a) \(x^2-1=0\Rightarrow\) \(x=\) @@-1@@, \(x=\) @@1@@

b) \(2x^2+4x=0\Rightarrow\) \(x=\) @@-2@@, \(x=\) @@0@@

c) \(x^2-3x=0\Rightarrow\) \(x=\) @@0@@, \(x=\) @@3@@

d) \(x^2-16=0\Rightarrow\) \(x=\) @@-4@@, \(x=\) @@4@@

Su navegador no es compatible con esta herramienta.

Resolviendo ecuaciones completas

En caso de que \(b\neq 0\) y \(c\neq 0\), la ecuación de segundo grado se dice que es completa y se resuelve aplicando la fórmula

\[x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\]

Por ejemplo,

\[2x^2+x-1=0\]

Es una ecuación completa por no faltarle ningún término.

Se resuelve sustituyendo los valores a=2, b=1 y c=-1 en la fórmula. Mira la solución paso a paso en la imagen. No te olvides de que los números a, b y c siempre llevan asociados un signo.

En este tipo de ecuaciones no siempre vas a obtener dos soluciones diferentes. Si la raíz cuadrada da 0 obtendrás una única solución que se dice que es doble. También puede ocurrir que tengas que calcular la raíz cuadrada de un número negativo. Como esto no es posible usando números reales, se dice que la ecuación no tiene solución en \(\mathbb{R}\).

En la piel del ladrón

Con el objetivo de desarrollar vuestra capacidad estratégica os proponemos que, por una vez, os pongáis en el lugar de un ladrón.

Imaginad que acabáis de robar un valioso cargamento y tenéis que ocultarlo en pequeños cofres que enterraréis para que otros compañeros detectives no los encuentren. Pero cuidado, en la siguiente ronda seréis vosotros quienes intentéis localizar los escondites de vuestros contrincantes. ¡Preparaos para pensar como ladrones mientras actuáis como detectives!

Poneos por parejas dentro del equipo y descargad los tableros de juego clicando sobre la imagen.

Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0