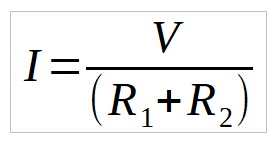Saltar la navegación

8. Circuitos en serie

Circuitos en serie

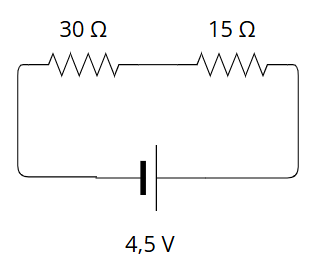
La palabra serie significa: "Conjunto de cosas que se suceden unas a otras". Un circuito en serie es aquel en el que los elementos se colocan uno a continuación del otro. El polo negativo de cada elemento (del que salen los electrones) se conecta al positivo del siguiente (por el que entran los electrones)

En un circuito en serie, los electrones van pasando en igual cantidad y a la misma velocidad por un elemento tras otro.  La intensidad en un circuito en serie es la misma en todos sus puntos.


Simulación de PhET Interactive Simulations, University of Colorado Boulder. https://phet.colorado.edu. CC-BY-4.0 
 

Pilas en serie

Cuando se conectan dos pilas en serie, los electrones pasan primero por una, ganando la energía que les da esa pila, y luego por la otra, ganando la energía que les da la segunda pila. La energía que obtienen en total es la suma de ambas:

V = V1 +V2

Para calcular la intensidad que pasa por el circuito se aplica la ley de Ohm:

Fíjate como, en la figura, el borne positivo de una pila (la línea larga del símbolo de la pila) está conectado con el borne negativo de la otra (la línea corta), como corresponde a la conexión en serie.

Audio::

Ejemplo

Lee y completa los huecos.

Un circuito en serie está formado por dos pilas de 12 V y un motor, por el que circula una intensidad de 4 A. Calcula la resistencia del motor.

El voltaje total al que está conectado el motor es la suma de los voltajes de las dos pilas, al estar estas conectadas en serie: V = V1 + V2 = + = 24

Según la ley de Ohm: R = V / I = / =  Ω

Audio: 

Habilitar JavaScript

Resistencias en serie

En un circuito con resistencias conectadas en serie, los electrones las irán atravesando todas, una a continuación de la otra. La resistencia total del circuito será la suma de las resistencias:

R = R1 + R2

Se calcula la intensidad que pasa por el circuito teniendo en cuenta esto y la  la ley de Ohm:



Hay que tener en cuenta que no se va a perder la misma energía en todas las resistencias a no ser que sean iguales. Si una resistencia es mayor que la otra se perderá más energía en esa. 

La energía por unidad de carga que se pierde en cada una de ellas (diferencia de potencial) será, según la ley de Ohm:

En la resistencia 1:        V1 = I · R1

En la resistencia 2:       V2 = I · R2

V1 y V2 son la diferencia de potencial que existe entre ambos lados de cada resistencia (figura). Como la energía total por unidad de carga que llevaban los electrones al salir de la pila (V) la tienen que emplear en atravesar las dos resistencias y volver a la pila: 

V = V1 + V2

Audio: 

Ejercicio paso a paso.

Calcula la resistencia equivalente y la intensidad de corriente que circula por el circuito de la figura. Completa los huecos que faltan.

Datos: R1 = 30 Ω, R2 =   Ω, V = 4,5 V

Incógnitas: R, I

Fórmulas:

Resistencia total o equivalente del circuito en serie: R = R1 + R2

Ley de Ohm: V = · R

Despejamos las fórmulas que lo requieran. En este caso, queremos calcular I, así que la despejaremos de la ley de Ohm:

I =

Sustituir los datos:

R = 30 + 15 = 45  Ω

I = V / R = / = 0,1

Audio: 

Habilitar JavaScript

Ejercicio

A una pila de 9 V se conectan dos resistencias en serie, una de 0,04 kΩ y otra de 60 Ω.

a) Calcula la diferencia de potencial en los extremos de la resistencia de 0,04 kΩ y la intensidad que circula por el circuito.

b) ¿Qué energía por unidad de carga se pierde en la otra resistencia?

Completa los huecos.

Datos: R1 = 0,04 kΩ =  Ω,                2 =    Ω,               = V

Incógnitas:   a) V1 e       b) V2

Fórmulas circuito en serie: 

= R1 + R2                        V = I · R                        V1 = I · R1                     V2 = I · R2

Despejamos las fórmulas que lo requieran para poder calcular las incógnitas:  I =   / 

Sustituimos los datos:

a) R = 40 + = 100  Ω

I = V / R = / = 0,09

Fíjate en el orden en el que hemos resuelto el problema a pesar de que lo primero que nos piden es V1:

1. Hemos calculado R porque era necesaria para calcular l.

2. Hemos calculado I porque era necesaria para calcular V1 y V2

3. AHORA podemos calcular la diferencia de potencial entre los extremos de la resistencia de 40 Ω (V1):

V1 = I · R1 = · = 3,6 V

b) En la otra resistencia: V2 = I · R2 = · = 5,4 V

Audio: 

Habilitar JavaScript

Creado con eXeLearning (Ventana nueva)