4.3. Bisectriz de un ángulo
Bisectriz
La bisectriz de un ángulo es la recta que pasa por su vértice y lo divide en dos ángulos iguales
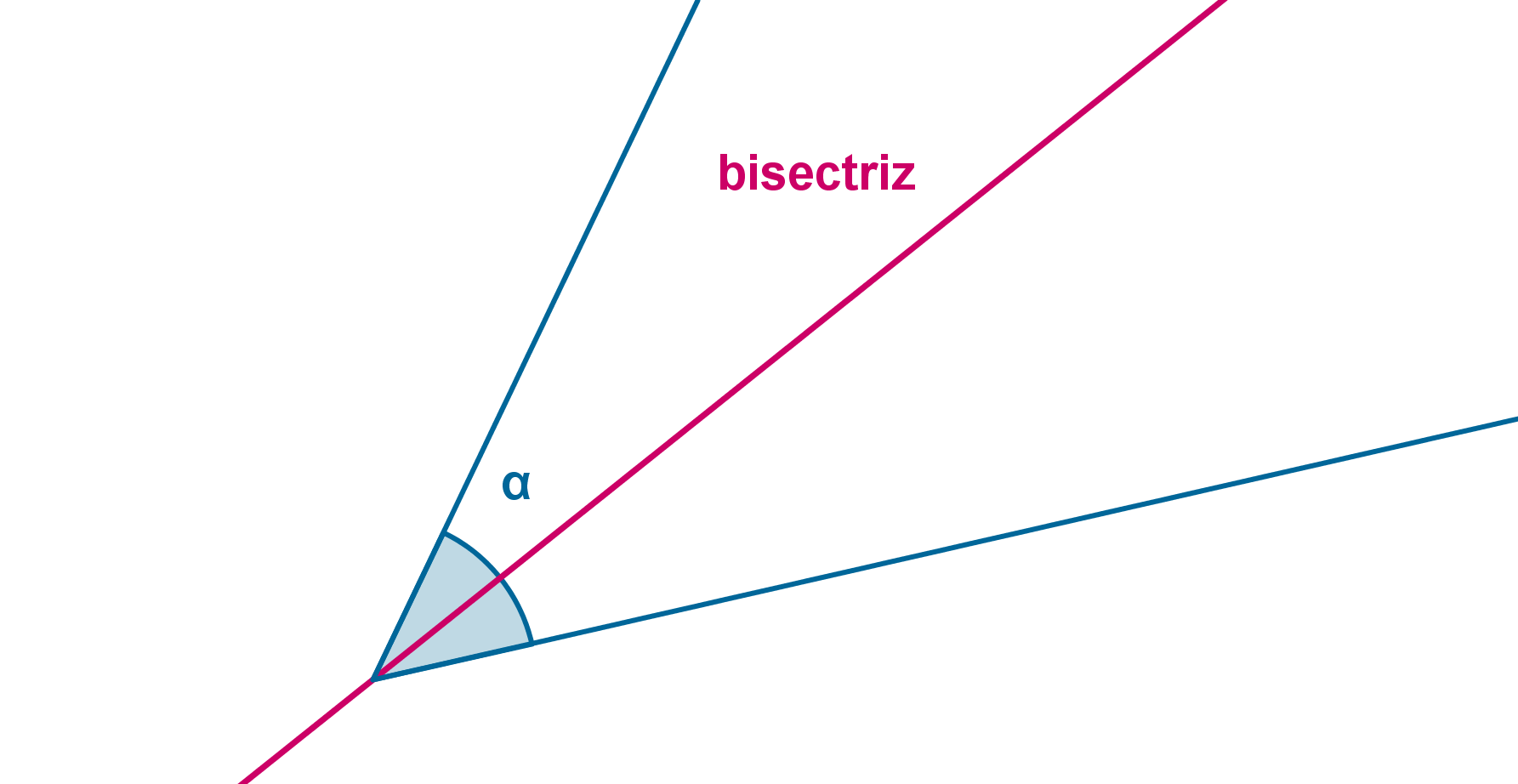
Actividad 1
Dibuja la bisectriz del ángulo α a partir de los puntos A, P y Q utilizando el botón "bisectriz" 
Guarda el archivo como "bisectriz_a_partir_de_tres_puntos".
Dibuja la bisectriz del ángulo α a partir de las semirrectas que lo delimitan utilizando el botón "bisectriz"
Guarda el archivo como "bisectrices_a_partir_de_dos_semirrectas".
¿Encuentras alguna diferencia entre las dos formas de hacerlo? Explícalo.
Nota:
¡Ojo! En la barra de herramientas que aparece por defecto al iniciar GeoGebra, el botón "bisectriz" se encuentra en el menú desplegable del botón "recta perpendicular" 
Actividad 2
En el siguiente applet aparecen un ángulo, las dos semirrectas que lo forman, r y s, y un punto Q. Se muestran también las distancias entre el punto Q y las dos semirrectas.
Mueve el punto Q sin mover las semirrectas y ve fijándote en las distancias que aparecen.
¿Qué sucede cada vez que pasas por un punto que esté a la misma distancia de las dos semirrectas que forman el ángulo?
Localiza varios de estos puntos y ve fijándote en el rastro que dejan.
¿Forman una curva o están alineados?
Marca la casilla "Ver bisectriz". ¿Con qué coincide?
El punto P es un punto de la bisectriz, muévelo y fíjate en su distancia a las semirrectas r y s.
Actualiza la vista gráfica y mueve las dos semirrectas arrastrando los puntos que están al lado de sus nombres y a continuación vuelve a mover el punto P de la bisectriz.
¿Puedes enunciar alguna propiedad que cumplan todos los puntos de la bisectriz?
Conclusiones actividad 2
Todos los puntos que están a la misma distancia de las dos semirrectas que forman un ángulo están alineados.
Esa línea recta es precisamente la bisectriz del ángulo.
Propiedad de la bisectriz
Todos los puntos de la bisectriz de un ángulo equidistan de los lados del ángulo.