¿Qué tienen en común?
En las bibliotecas, para organizar los libros, se ponen unas letras comunes que los identifican.
Vas a estudiar cómo obtener múltiplos y divisores comunes a varios números, y cómo elegir uno de ellos.
m.c.d.
El máximo común divisor de dos o más números es el mayor de sus divisores comunes.
Por ejemplo, en la imagen está el m.c.d. de 8 y 6 que es 2.
Ejemplos
Comenzamos buscando los divisores de los números 24, 18 y 12, para calcular el máximo común divisor, m.c.d. (24, 18, 12).
Divisores de 24 = {1, 2, 3, 4, 6, 12, 24}
Divisores de 18 = {1, 2, 3, 6, 9, 18}
Divisores de 12 = {1, 2, 3, 4, 6, 12}
Siempre entre llaves y en orden de menor a mayor.
Los números que se repiten están de color azul, tienen que coincidir en las tres descomposiciones.
Los números que se repiten son el 2, el 3 y el 6.
De todos los divisores que se repiten (comunes), nos quedamos con el mayor de todos (el máximo), que en este caso es el 6.
El máximo común divisor de 24, 18 y 12 es el número 6.
m.c.d. (24, 18, 12) = 6.
Si el único factor común es el 1 estos números son primos entre sí.
m.c.m.
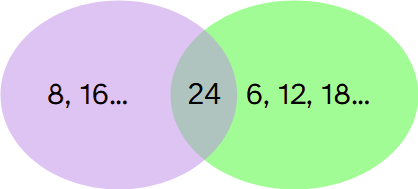El mínimo común múltiplo de dos o más números es el menor de sus múltiplos comunes.
Por ejemplo, en la imagen está el m.c.m. de 8 y 6 que es 24.
Es más sencillo hallar el máximo común divisor que el mínimo común múltiplo, porque múltiplos hay infinitos y divisores hay un número finito.
Ejemplos
Hallar el m.c.m. (6, 4, 3).
Paso 1: Busca los múltiplos comunes de los tres números.
Múltiplos de 6 = {0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60… }
Múltiplos de 4 ={ 0, 4, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52… }
Múltiplos de 3 = {0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42… }
Observa que son las tablas de multiplicar del 6, del 4 y del 3.
Se repiten los números: 12, 24, 36...
De todos los múltiplos que se repiten (comunes) en las tres tablas, nos quedamos con el menor de todos: el mínimo, que en este caso es el 12.
El mínimo común múltiplo de 6, 4 y 3 es el número 12.
m.c.m. (6, 4, 3) = 12.
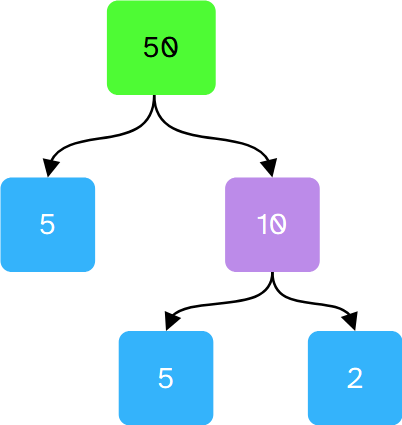A continuación verás un método para hallar el máximo común divisor y el mínimo común múltiplo de dos o más números, utilizando la descomposición en factores primos de cada uno de ellos.
