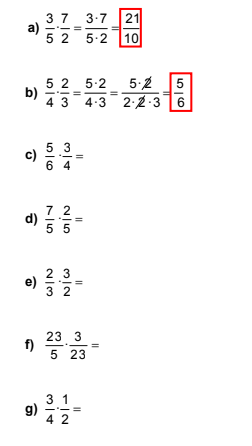
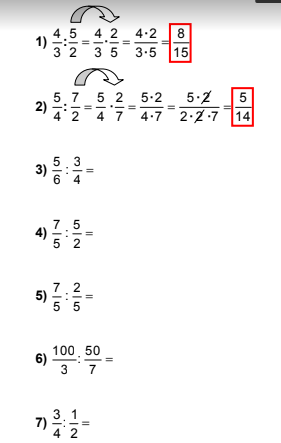
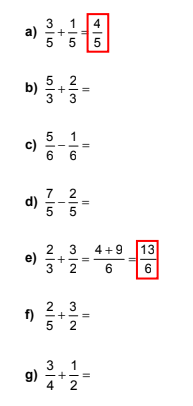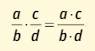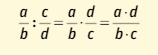De cotío, empregamos expresións que teñen relación coas fraccións, tres cuartos de hora, litro e medio de auga, dous tercios da poboación etc.
Observa a seguinte imaxe dun encoro de Zamora (Ricobayo) no mes de xaneiro de 2018. Sabemos que neste momento, este embalse almacena 1000 hm3 de auga.

Temos recollida a información de como vai aumentando a cantidade de auga no encoro, de xeito que sabemos que no mes de febreiro houbo unha sexta parte máis de auga que en xaneiro... como podemos expresalo? pois cunha fracción como a que vemos na seguinte figura, na que o 1 é o numerador, e 6 é o denominador, que sempre será ≠ 0
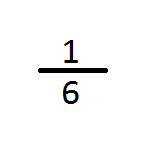
Unha fracción pódese interpretar de varias formas:
- Como partes da unidade: queda 1/6 de biscoito
- Como cociente entre dous números: repartir 6 laranxas entre 8 nenos, 6/8
- Como fracción de cantidade: 2/5 de 30 coches son diésel, co cal 2/5.30 = 2.30/5 =12
Fraccións equivalentes
Dúas fraccións son equivalentes cando representan a mesma parte da unidade.
Sabemos se son equivalentes, cando os seus produtos cruzados son iguais.
Por exemplo:
Son equivalentes 4/6 e 8/12?
Os seus produtos cruzados son 4 .12 = 8. 6 e nos dous casos o resultado é 48, co cal si son equivalentes.
A expresión gráfica o confirma:
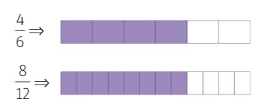
Para obter fraccións equivalentes a unha dada, temos que multiplicar ou dividir numerador e denominador (os seus termos) polo mesmo número
Cando os termos dunha fracción non poden dividirse máis entre un mesmo número, falamos de fraccións irreducibles.
Por exemplo Buscamos unha fracción equivalente a 2/10 que tamén sexa irreducible:
Dividimos entre 2 ambos termos e obtemos 1/5, fracción equivalente, porque 2.5 =1.10 =10 e que non se pode reducir máis.