3.3. Tablas, números... ¡y acción!

Primera plana: avance del virus 2XYZ

Hoy llegamos a la redacción y nos encontramos con algo inesperado... Una noticia impactante está cogiendo carácter "viral" en estos momentos. Sí, nunca mejor dicho, además sobre un virus...

Domingo 9 de marzo

El Mathington Post

PRIMERA PLANA

Enorme preocupación por el avance del virus 2XYZ

Las autoridades sanitarias han confirmado un aumento muy preocupante del número de contagios de 2XYZ en los últimos días. Los primeros casos en España se detectaron el pasado domingo, justo hace una semana, y ya suman hoy más de 50. Las cifras siguen creciendo.

Se están multiplicando y preocupa cómo contener la enfermedad del virus.

Seguimiento en tiempo real: Mantén actualizada tu información en El Mathington Post con las noticias en tiempo real y nuestra excepcional cobertura.

El famoso virus 2XYZ está siendo portada en todos los diarios. Se está expandiendo a pasos agigantados, todas las agencias están recopilando datos y están las redacciones que arden.

El Mathington, como buen periódico de carácter eminentemente matemático, está cuidando mucho el enfoque de esta noticia. Aquí son imprescindibles las gráficas para intentar entender cómo es la evolución del avance del virus.

Todos los días (incluso cada hora o cada minuto), hay nuevos datos sobre cómo avanza la enfermedad, y las autoridades sanitarias tienen que definir medidas a adoptar que son muy severas.

Para tomar la mejor decisión deberás analizar los datos, entender lo que dicen y buscar las medidas más efectivas.

Puedes ayudar a entender mejor lo que está pasando si utilizas gráficas, junto con datos bien explicados.

Lectura facilitada

Hoy llegamos a la redacción y nos encontramos con una nueva noticia.

Un virus 2XYZ está siendo portada en todos los diarios

El Mathington, aborda la noticia con gráficas sobre la evolución del virus.

Todos los días hay nuevos datos..

Para tomar la mejor decisión deberás analizar los datos.

Puedes ayudar a entender lo que está pasando si utilizas gráficas, junto con datos.

Tablas de datos para definir funciones

En muchas ocasiones tendrás una tabla con datos tomados de la observación de un fenómeno; en este caso, el avance número del número de contagios del virus.

Algunas se pueden modelizar y aproximar por una función, esto ayudará a predecir cómo puede evolucionar en el futuro.

Fíjate en el ejemplo de los datos de avance del virus 2XYZ en los primeros días de propagación.

Primero debes que saber qué información tienes:

Datos de propagación del virus 2XYZ
x (día)	y (nº de casos)
1	2
2	4
3	8
4	16
5	32

A partir de esta tabla con datos, puedes representar la gráfica de estos puntos, y tendrás una idea de la relación entre los días y el avance del virus.

Esta sería la gráfica:

Gráfica función

Uy, uy, uy, ¿esto es una función? ¿Y qué quiere decir?

En este caso sí, es una función, y lo que quiere decir es que el virus se propaga muy rápido...

Si te fijas, verás que el número de nuevos casos es una potencia de base dos: 2⁰, 2¹, 2²..., algo que ya viste en el tema 1.

Cuando ocurre esto se dice que tiene un crecimiento exponencial (los días son el exponente).

¿Qué significa?

¿No es mucho? ¿Estarán bien los datos? Sí, es cierto, es un crecimiento muy pronunciado.

Personas expertas en virología indican que es bastante común que un virus tenga este tipo de comportamiento al principio y también es bastante peligroso. Ten en cuenta que si hoy hay 2 personas contagiadas que no lo saben y salen a la calle, si cada una contagia a otras 2, mañana tenemos 4 contagiadas. Y al día siguiente esas 4 habrán contagiado a 8, y así sucesivamente.

Lo importante es que, analizando estos datos, se pueden tomar medidas, y "revertir" esta situación para frenar un poco al virus y que el contagio se reduzca.

¡Fíjate, precisamente tenemos noticias! Acaba de llegar un teletipo de las agencias de noticias diciendo que se han tomado dos medidas muy importantes: se ha decretado el uso de mascarillas para evitar la propagación del virus y se recomienda a toda la población realizarse un análisis al mínimo síntoma para detectar cuanto antes los casos de contagio.

Seguramente, nuestras tablas de datos serán diferentes en los días sucesivos, ¿no te parece?

Resumen

Hemos dado los siguientes pasos:

Pensar cuál es el objetivo: entender la propagación del virus.
Construir la función que va a estudiar, la evolución del número de contagios diarios a partir de:
- La variable independiente, que va a ser el tiempo expresado en días.
- La variable dependiente, que va a ser el número de "nuevos casos" que se han registrado cada día.
- La tabla de valores, que consistirá en poner todos esos datos juntos formando pares ordenados (tiempo en días, número de casos diarios).
Dibujar la gráfica representando los valores en los ejes de coordenadas (x = número del día, y = número de casos nuevos), y unir los puntos con segmentos rectilíneos.

Novedades en deportes

Saltamos ahora a la sección de deportes.

Vas a analizar los datos de la gran Ana Peleteiro que, como sabrás, es atleta de triple salto. Su temporada es fantástica y en el periódico se va a publicar una gráfica analizando los saltos en sus últimos días de entrenamiento antes de una gran cita.

La gráfica está sin hacer, ¿te pones con ello?

Aquí están los datos de los saltos en 12 días consecutivos.

Representa en tu cuaderno la gráfica de esta función y, si te atreves, haz un pequeño análisis de cómo ha sido su evolución.

Día	1	2	3	4	5	6	7	8	9	10	11	12
Marca (m)	13,90	13,98	14,10	14,25	14,15	14,30	14,50	14,55	14,60	14,70	14,85	14,80

Ciencia y naturaleza

Un estudio ginecológico recoge datos del tamaño del feto (antes de que nazca un bebé) durante los meses de la gestación.

Son los siguientes:

Mes	2	3	4	5	6	7	8	9
Talla (cm)	4	8	15	24	29	34	38	42

Solicitan la ayuda del periódico para realizar la gráfica de la función a partir de la tabla de datos.

Funciones definidas mediante fórmulas

¿Te suena esta ecuación? ¿Crees que tiene relación con las funciones?

Investiga un poco sobre su significado y comenta con tu equipo las conclusiones.

Ya has visto que, en muchas ocasiones de la vida real (en las noticias, en la ciencia, etc.), hay muchos datos y para entenderlos se utilizan las funciones.

A veces tenemos la suerte de poder "relacionar" las variables x e y en una expresión que llamamos ecuación.

¿Cómo funciona eso de la fórmula?

En el apartado 3.1., en el ejercicio "Una cuestión de estilo", calculaste el dinero que tendría María, semana a semana, porque sabías lo que tenía al principio (15 euros) y cuánto ahorraba semanalmente (2 euros).

Esto te permitió escribir una fórmula que obtenía el dinero en función del tiempo:

f(x) = 15 + 2x, o también, y = 15 + 2x

La fórmula o ecuación de una función es una forma de escribirla basada en las operaciones que hay que hacer con x para hallar y.

Por lo tanto, se pueden hallar todas las parejas de valores que necesites.

A partir de ellas podrás también construir la tabla de valores y la representación gráfica.

Representando la función

Tabla de valores de la función

¿Qué valores vas a representar? ¿Cuántos tienes que poner?

Depende de la función, algunas son más simples y llega con dos valores (por ejemplo, las rectas).

Por ejemplo, en el caso del problema de los ahorros de María, cuya fórmula es f(x) = 2x + 15, una tabla posible es:

x semanas	f(x) euros
0	15
5	25
10	35

semanas

f(x)

euros

Reflexiona, ¿tendría sentido dar a la x valores negativos? ¿Por qué?

Gráfica de la función

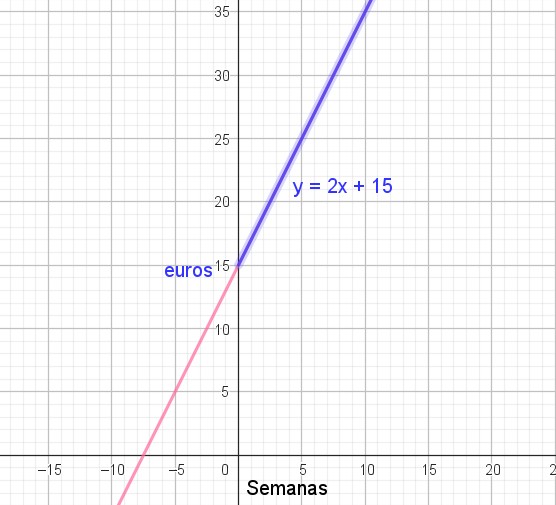Gráfica de y=2x+15 Como ya has visto en ejemplos anteriores, para hacer la gráfica simplemente tienes que representar cada uno de los puntos (x,y), y unirlos.

La gráfica de una función es el conjunto de todos los puntos (x, f(x))

Está marcada en rojo la parte en la que los valores de x son negativos, ¿crees que debe dibujarse, sí o no?

Procedimiento paso a paso

Algoritmo para representar una función En resumen, este es el procedimiento para representar funciones a partir de su fórmula, punto a punto.

1. Construyes los puntos (x, f(x)) que formarán la tabla de valores.

1.1. Elige un valor de x.

1.2. Calcula f(x).

1.3. Representa el punto (x, f(x)).

2. ¿Tienes suficientes puntos?

En caso negativo, repite el paso 1.

En caso afirmativo, une los puntos mediante una recta (si es posible), o bien mediante una curva lo más "suave" posible.

Practica la representación de funciones

Representa gráficamente en tu cuaderno las siguientes funciones, dando los valores que te sugerimos a continuación:

a) \( y=-x+5 \), con los valores \(x=-2\), \(-1\), \(0\), \(1\), \(2\).

b) \( y=\dfrac{x+3}{2} \), con los valores \(x=-2\), \(-1\), \(0\), \(1\), \(2\).

c) \( y=x(2-x) \), con los valores \(x=-2\), \(-1\), \(0\), \(1\), \(2\), \(3\), \(4\).

Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0