Moviendo ficha
Ahora que ya sabes situar puntos en una cuadrícula puedes subir un peldaño más y aprender a moverlos.
Es el momento de aprender los movimientos en el plano.
Se trata de cambiar figuras de sitio sin alterar su forma.
Vas a empezar por el más sencillo, la traslación, luego verás el giro y finalmente la reflexión.
Traslación: sigue la flecha
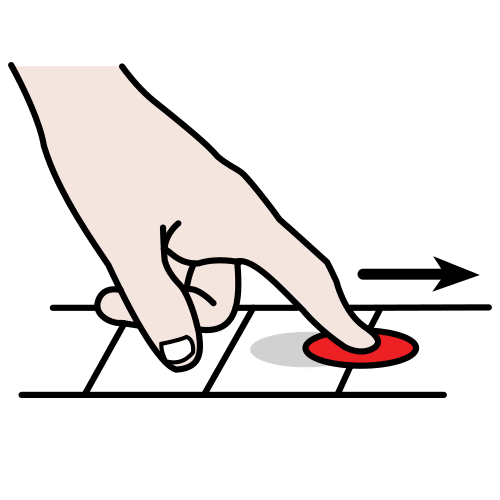Observa la mano de la imagen.
Está moviendo una ficha en una dirección (siguiendo la línea) y en un sentido (hacia la derecha).
A este movimiento se le llama traslación.
Para trasladar una ficha necesitas saber en qué dirección y en qué sentido la vas a mover (una flecha).
En la vida real, cuando te mueves siguiendo una flecha, estás haciendo una traslación.
Giro: abriendo puertas
En tu día a día haces giros constantemente: para abrir una puerta, al cruzar una calle...
Piensa cómo abres la puerta:
1. Metes la llave buscando el centro.
2. Giras un ángulo hacia un lado.
Estos son los dos elementos importantes de un giro: el centro y el ángulo, este último con un sentido (hacia la derecha o hacia la izquierda).
El giro es un movimiento que tiene como elementos importantes un centro y un ángulo orientado.
El giro también se llama rotación.
En la vida real hay figuras que contienen elementos girados. Por ejemplo: el rosetón de una catedral, los pétalos de una margarita...
¿Se te ocurren más figuras con esta cualidad?
Un giro especial: 180º
Un ejemplo de giro muy especial es el giro de 180º.
Es interesante porque aparece mucho en la vida real: en balcones, ventanas, logos...
A este tipo de giro se le da el nombre de "simetría central".
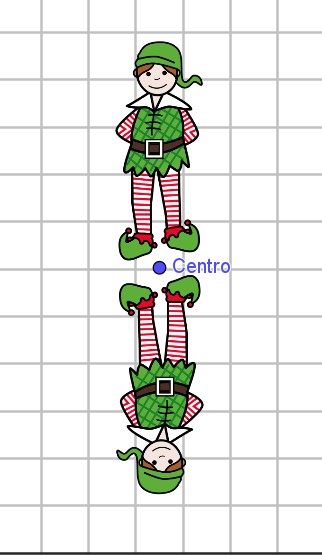
En el dibujo puedes ver un ejemplo de un elfo al que se le ha dado un giro de 180º.
Observa que el de arriba tiene el final del gorro hacia a su izquierda y el de abajo también.
Los giros no cambian la orientación de las figuras.
Prueba hacer giros de otras figuras conocidas, por ejemplo un triángulo rectángulo.
Reflexión: efecto espejo
Este movimiento es más complicado porque consiste en hacer un "efecto espejo".
Observa estas dos imágenes de un motorista. Son idénticas pero en la primera la mano levantada es la izquierda y en la segunda la mano levantada es la derecha.
Cada una de ellas es una reflexión de la otra.
Pero hay algo más...
¿Dónde estaría el espejo? ¿En qué lugar aparece el motorista reflejado?
Marca una línea recta justo en el medio de las dos figuras. Es el eje de reflexión.
Si doblamos por esa línea las dos figuras se superponen.
La reflexión es un movimiento que coloca la figura original y la reflejada a la misma distancia de un segmento, el eje de reflexión.
La reflexión también se llama simetría axial (porque se refleja siguiendo el eje).
A veces, cuando se habla de simetría sin decir nada más, se refieren a este movimiento en "espejo".
Observa que, tanto la traslación como el giro, no tienen ese efecto espejo.
Robi limpia la clase trasladándose en distintas direcciones que tiene programadas antes de empezar.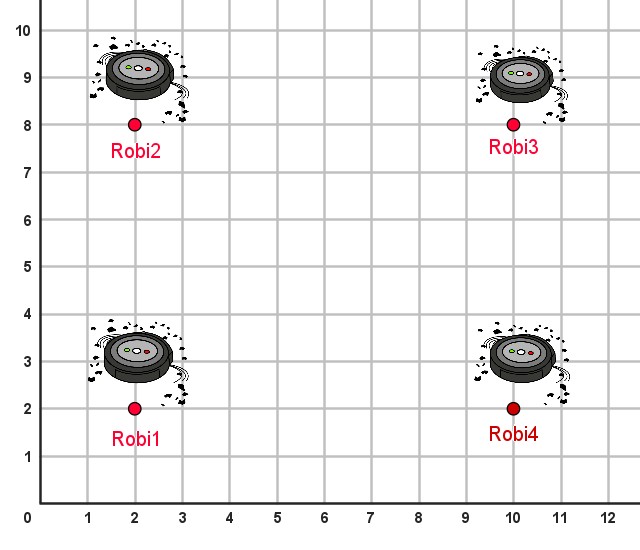
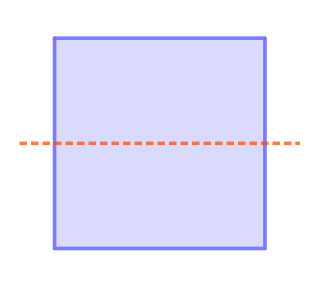
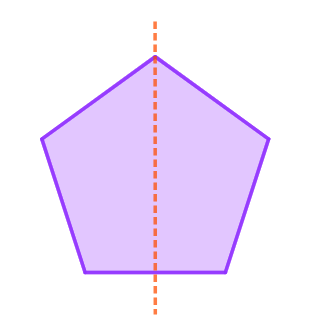
¿Se te ocurren otros ejes de simetría para un cuadrado? ¿Para un pentágono regular? ¿Y si fuese un rectángulo en lugar de un cuadrado?
¿Y en la vida real? ¿Hay figuras con ejes de simetría?
