A densidade

Entre as propiedades específicas da materia (temperaturas de fusión e ebullición, dureza, conductividade...), imos centrarnos agora na densidade... e para iso, veremos primeiro este video

Como se explica no vídeo, a densidade fai unha relación entre a masa dos corpos e o seu volumen, tal e como expresamos na fórmula:

Deste xeito..., imaxinemos tres canicas idénticas en volumen, a densidade de cada unha delas variará en función da masa que teña cada unha dentro deste mesmo volume.

E ao revés, se temos unha mesma masa, por exemplo 1 kg de ferro e 1 kg de palla...seremos capaces de telos nun mesmo volume?

É evidente que non... a palla ocupará moito máis volume que o ferro

As unidades nas que se expresa a densidade no S.I, son os g/cm³

Imos resolver un problema sinxelo de densidades:

Calcula a densidade dun material que ten de masa 800 g e o seu volume é 40 cm³

Como sabemos, a densidade é o cociente entre a masa e o volume... polo tanto, só temos que dividir 800 g entre 40 cm³.

O resultado son 20 g/cm³

Trata de resolver o problema

Cal será o volume de 2,13 kg de estaño se a súa densidade é de 7,28 g/cm^³

En primeiro lugar pasamos os 2,13 kg a g: 2130 g

Despexando o volume da fórmula da densidade temos que V= m/d, co cal temos que dividir 2130g/7,28 g/cm³

A resposta é 292,58 cm³

Aplicación práctica da densidade---A corona dourada

Conta unha historia que non se sabe ben canto ten de certo, que o grego Arquímedes de Siracusa (en grego antigo Ἀρχιμήδης Arkhimḗdēs; Siracusa (Sicilia), ca. 287 a. C.-ibidem, ca. 212 a. C.).

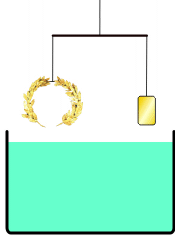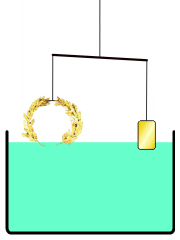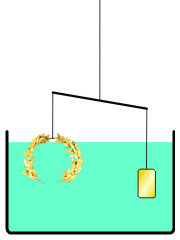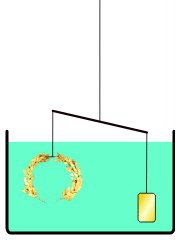
Físico, enxeñeiro, inventor, astrónomo e matemático inventou un método para determinar o volume dun obxecto cunha forma irregular. Dacordo con Vitruvio, Hierón II ordenou a fabricación dunha nova coroa con forma de corona triunfal, e pediulle a Arquímedes determinar se a coroa estaba feita só de ouro, ou pola contra, o orfebre engadira prata na súa realización para enganalo. Arquímedes tiña que resolver o problema sen estropear a coroa, así que non podía fundila e convertila nun corpo regular para calcular a súa masa e volume, e a partir de ahí, a súa densidade. Un día, tomando un baño notou que o nivel da auga subía na bañera cando entraba, e así deuse conta de que ese efecto podería ser usado para determinar o volume da coroa. Debido a que a auga non se puede comprimir, a coroa, ao ser sumerxida, desprazaría unha cantidade de auga igual ao seu propio volume. Ao dividir o peso da coroa polo volume de agua desprazada poderíase obter a densidade da coroa. A densidade da coroa sería menor que a densidade do ouro se outros metais menos densos lle foran engadidos. Cando Arquímedes, durante o baño, deuse conta do descubrimento, dise que saiu correndo núo polas rúas tan emocionado que esqueceu vestirse. Segundo o relato, na rúa gritaba «¡Eureka!» (en grego antigo: «εὕρηκα» que significa «¡Atopeino!»).

A densidade do ouro

Imaxinemos que a masa da coroa do conto anterior era de 1 kg, e que o volume calculado por Arquimedes foi de 64,8 cm³. Cal é a densidade que calculo Arquímedes en g/cm³? Tendo en conta que a densidade do oro é de 19,32 g/cm³... enganou orfebre ao Rei?

Pois... parece ser que o orfebre non era de fiar, xa que a densidade que podemos calcular con estes datos, é de 15,43 g/cm³(utilizando a fórmula d=m/v). Probablemente reemplazou unha cantidade por prata, que ten unha densidade bastante menor, de 10,5 g/cm³.

BY-NC-SA